Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам 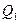 и
и  обратно пропорциональна квадрату расстояния r между ними.
обратно пропорциональна квадрату расстояния r между ними.

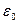 - диэлектрическая проницаемость вакуума.
- диэлектрическая проницаемость вакуума.
Напряженность электростатического поля 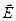 в данной точке есть физическая величина, определяемая силой
в данной точке есть физическая величина, определяемая силой  , действующей на пробный единичный заряд
, действующей на пробный единичный заряд 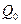 , помещенный в эту точку поля.
, помещенный в эту точку поля.
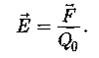
Поток вектора напряженности электростатического поля сквозь замкнутую поверхность S:
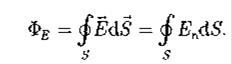
Принцип суперпозиции электростатических полей: напряженность результирующего поля создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
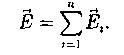
Электрический момент диполя:
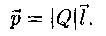
Электрический диполь – система двух равных по модулю разноименных точечных зарядов (+Q,-Q), расположенных на расстояние 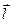 друг от друга (
друг от друга (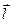 направлен от отрицательного заряда к положительному).
направлен от отрицательного заряда к положительному).
Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленных на диэлектрическую проницаемость вакуума.
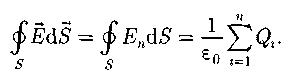
Объемная, поверхностная и линейная плотности зарядов:
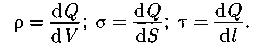
Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью:
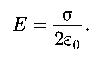
Напряженность поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями:

Напряженность поля, создаваемого равномерно заряженной сферической поверхностью:
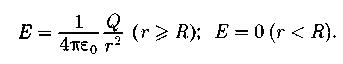
Напряженность поля, создаваемого объемно заряженным шаром:

Напряженность поля, создаваемого бесконечной нитью, равномерно заряженной с линейной плотностью заряда  :
:
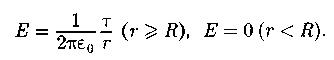
Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура L:
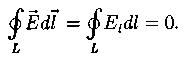
Потенциал электростатического поля в какой либо точке есть физическая величина, определяемая работой по перемещению единичного положительного заряда силами поля при удалении его из данной точки поля на бесконечность.
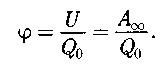
Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля по перемещению единичного положительного заряда из точки 1 в точку 2.
Связь между потенциалом электростатического поля и его напряженностью:
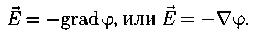
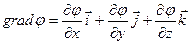
Поляризованность (вектор поляризации) - дипольный момент единицы объема:
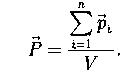
При помещении диэлектрика объемом V во внешнее поле он поляризуется, т.е. приобретает дипольный момент 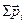 , где
, где 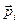 - дипольный момент i -той молекулы.
- дипольный момент i -той молекулы.
Связь между векторами 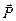 и
и 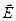
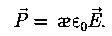
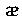
 - диэлектрическая восприимчивость вещества. (Для большого класса диэлектриков поляризованность
- диэлектрическая восприимчивость вещества. (Для большого класса диэлектриков поляризованность 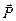 линейно зависит от напряженности поля).
линейно зависит от напряженности поля).
Связь между диэлектрической проницаемостью среды и диэлектрической восприимчивостью вещества:
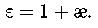
Связь между векторами электрического смещения и напряженностью электростатического поля:
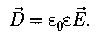

Теорема Гаусса для электростатического поля в диэлектрике:
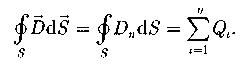
Электрическая емкость уединенного проводника:

Электрическая емкость шара радиуса R:
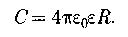
Электрическая емкость плоского конденсатора:
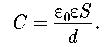
S;d - площадь пластины, расстояние между пластинами.
Электрическая емкость цилиндрического конденсатора длиной l и радиусами цилиндров 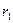 и
и 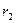 (
(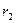 >
> 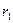 ):
):

Электрическая емкость сферического конденсатора (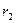 >
> 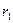 ):
):
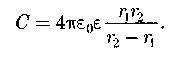
Электрическая емкость параллельно соединенных конденсаторов:
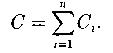
Энергия заряженного уединенного проводника с потенциалом φ:
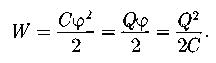
Энергия заряженного конденсатора с разностью потенциалов между пластинами Δφ:

Объемная плотность энергии электростатического поля:
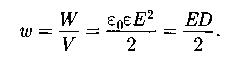
W- энергия электростатического поля в объеме V.
Сила тока: скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени.
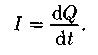
Электродвижущая сила, действующая в цепи: физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда.
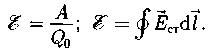
Закон Ома для однородного участка цепи: сила тока, текущего по однородному участку цепи прямо пропорциональна напряжению на концах проводника и обратно пропорциональна электрическому сопротивлению проводника.
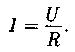
Закон Ома в дифференциальной форме:
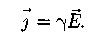
 |
- плотность тока (I/S), где S –сечение проводника. γ- удельная электрическая проводимость (γ=1/ρ; R= ρl/S; ρ - удельное сопротивление проводника ).
Мощность тока:
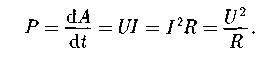
Закон Джоуля – Ленца:
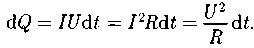
dQ – теплота, выделяющаяся в проводнике.
Закон Джоуля – Ленца в дифференциальной форме:

w - количество теплоты, выделяющееся за единицу времени в единице объема.
Закон Ома для неоднородного участка цепи (в интегральной форме ):
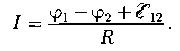
ЭДС 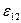 положительна, если способствует движению положительных зарядов в направлении 1-2.
положительна, если способствует движению положительных зарядов в направлении 1-2.
Правила Кирхгофа:
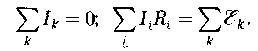
Коэффициент вторичной электронной эмиссии (отношение вторичных электронов к числу первичных):
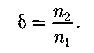
Магнитный момент контура с током:
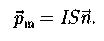
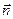 - единичный вектор нормали к поверхности контура (направлен по правилу буравчика по отношению к току); S – площадь поверхности контура; I – ток в контуре.
- единичный вектор нормали к поверхности контура (направлен по правилу буравчика по отношению к току); S – площадь поверхности контура; I – ток в контуре.
Вращательный момент, действующий на контур с током в магнитном поле:

Связь между индукцией  и напряженностью
и напряженностью 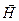 магнитного поля:
магнитного поля:
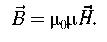
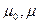 - магнитная проницаемость вакуума и среды.
- магнитная проницаемость вакуума и среды.
Закон Био – Савара – Лапласа для элемента dl проводника с током I:

 - радиус вектор, проведенный из элемента dl проводника в точку, где создается индукция
- радиус вектор, проведенный из элемента dl проводника в точку, где создается индукция 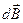 .
.
Магнитная индукция поля прямого тока на расстоянии R:
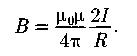
Магнитная индукция поля в центре кругового (радиусом R) проводника с током:
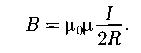
Напряженность магнитного поля внутри длинного соленоида:
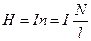
Закон Ампера ( сила, с которой магнитное поле действует на элемент dl проводника с током I:
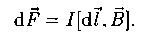
Магнитное поле свободно движущегося заряда:

 - радиус- вектор, проведенный от заряда Q, движущегося со скоростью
- радиус- вектор, проведенный от заряда Q, движущегося со скоростью 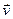 к точке наблюдения магнитного поля B.
к точке наблюдения магнитного поля B.
Сила Лоренца (сила, действующая на электрический заряд Q, движущийся в магнитном поле):

Холловская поперечная разность потенциалов:
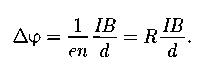
d;R – толщина пластинки; постоянная Холла, зависящая от вещества пластинки.
Теорема о циркуляции вектора  в вакууме (закон полного тока для магнитного поля в вакууме): циркуляция вектора
в вакууме (закон полного тока для магнитного поля в вакууме): циркуляция вектора  по произвольному замкнутому контуру в вакууме равна произведению магнитной постоянной
по произвольному замкнутому контуру в вакууме равна произведению магнитной постоянной  на алгебраическую сумму токов, охватываемых этим контуром.
на алгебраическую сумму токов, охватываемых этим контуром.
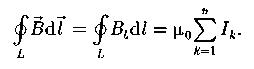
n – число проводников с токами, охватываемых контуром L произвольной формы.
Поток вектора магнитной индукции (магнитный поток) сквозь произвольную поверхность:
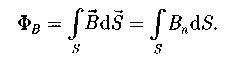
Теорема Гаусса для поля с магнитной индукцией  :
:

Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником:
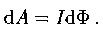
(где 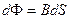 ).
).
Работа по перемещению замкнутого контура с током в магнитном поле
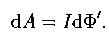
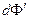 – изменение магнитного потока сквозь площадь, ограниченную контуром с током.
– изменение магнитного потока сквозь площадь, ограниченную контуром с током.
Закон Фарадея: ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
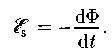
ЭДС самоиндукции:
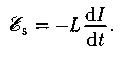
L – индуктивность контура.
Индуктивность бесконечно длинного соленоида, имеющего N витков:
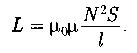
S;l -площадь сечения соленоида; длина соленоида.
Ток при размыкании цепи:

(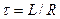 )
)
Ток при замыкании цепи:
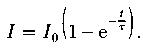
Энергия магнитного поля, связанного с контуром:

Объемная плотность энергии магнитного поля:
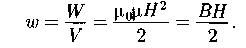
Намагниченность(магнитный момент единицы объема):

 - магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул.
- магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул.
Связь между векторами 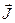 и
и 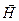
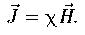
Связь между магнитной проницаемостью среды и магнитной восприимчивостью вещества:
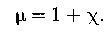
Теорема о циркуляции вектора  в веществе (закон полного тока для магнитного поля):
в веществе (закон полного тока для магнитного поля):
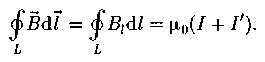
I; 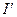 - алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.
- алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.
Теорема о циркуляции вектора 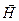 : Циркуляция вектора
: Циркуляция вектора 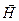 по произвольному замкнутому контуру L равн а алгебраической сумме токов проводимости, охватываемых этим контуром.
по произвольному замкнутому контуру L равн а алгебраической сумме токов проводимости, охватываемых этим контуром.
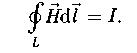
Плотность тока смещения:
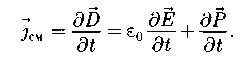
Полная система уравнений Максвелла в интегральной форме:
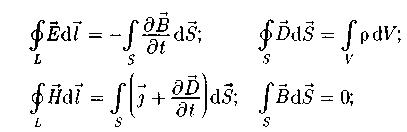
Полная система уравнений Максвелла в дифференциальной форме:
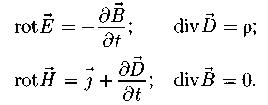
Колебания и волны
Уравнение гармонического колебания:
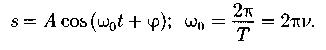
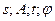 - координата колеблющейся точки; амплитуда; время; начальная фаза.
- координата колеблющейся точки; амплитуда; время; начальная фаза. 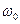 - циклическая частота.
- циклическая частота.
Дифференциальное уравнение свободных гармонических колебаний величины s:
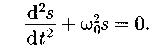
Период колебаний физического маятника:

Формула Томсона:
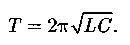
Дифференциальное уравнение свободных затухающих колебаний величины s:

Логарифмический декремент затухания:
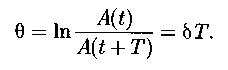
Добротность: 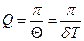 . В контуре:
. В контуре: 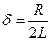 ,
, 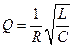 . Время релаксации(амплитуда уменьшается в е раз):
. Время релаксации(амплитуда уменьшается в е раз): 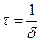 .
.
Дифференциальное уравнение вынужденных колебаний величины s:

Реактивное индуктивное сопротивление:

Реактивное емкостное сопротивление:
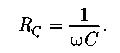
Полное сопротивление последовательно соединенных элементов RLC цепи:

Длина волны:
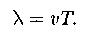
Уравнение плоской волны:
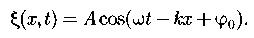
Уравнение сферической волны:
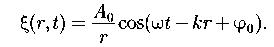
Фазовая скорость:
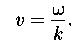
Волновое уравнение:

Групповая скорость:
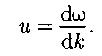
Уравнение стоячей волны:

Эффект Доплера в акустике:
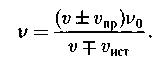
v – скорость распространения волны в среде;  - частота звуковой волны источника.
- частота звуковой волны источника. 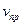 - скорость приемника,
- скорость приемника,  - скорость источника. (+ если взаимное приближение)
- скорость источника. (+ если взаимное приближение)
Вектор Умова-Пойнтинга:

Скорость распространения электромагнитных волн в среде:
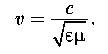
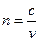
Плотность энергии упругой волны: 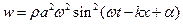 . Средняя по времени:
. Средняя по времени:
 . (В формуле: плотность среды, амплитуда волны, угловая частота).
. (В формуле: плотность среды, амплитуда волны, угловая частота).
Вектор Умова (плотность потока энергии = интенсивность): 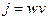 .
.
Оптика
Закон отражения света:

Закон преломления света:
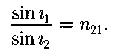
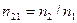 ; нумерация по ходу движения луча.
; нумерация по ходу движения луча.
Формула тонкой линзы:
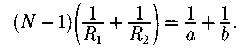
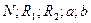 - относительный показатель преломления (отношение абсолютных показателей преломления линзы и окружающей среды); Радиусы кривизны второй и первой поверхности; Расстояние до предмета и изображения.
- относительный показатель преломления (отношение абсолютных показателей преломления линзы и окружающей среды); Радиусы кривизны второй и первой поверхности; Расстояние до предмета и изображения.
Поток излучения (отношение энергии излучения ко времени, Дж/с):
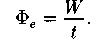
Энергетическая светимость, Вт/ 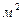 :
:
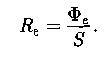
Энергетическая сила света: отношение потока излучения источника к телесному углу, Вт/ср (ср-стерадиан):
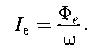
Энергетическая яркость: отношение энергетической силы света элемента излучающей поверхности к площади проекции этого элемента на плоскость, перпендикулярную к направлению наблюдения.
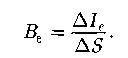
Показатель преломления среды:
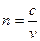
Оптическая длина пути (произведение геометрической длины пути света в данной среде на показатель преломления этой среды):

Оптическая разность хода:
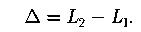
Условие интерференционных максимумов:
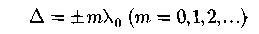
 - длина волны в вакууме.
- длина волны в вакууме.
Условие интерференционных минимумов:

Оптическая разность хода в тонких плоскопараллельных пленках в отраженном свете:
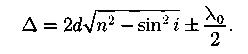
d;n;i- толщина пленки; показатель преломления пленки; угол падения и выхода из пленки.
Радиусы зон Френеля (радиусы засечки отличаются на полдлины волны. Амплитуда результирующего светового колебания в точке: 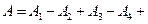 …, соответственно от первой, второй …зон.
…, соответственно от первой, второй …зон. 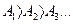
 .
. 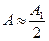 . Зонная пластинка (закрыты нечетные зоны)
. Зонная пластинка (закрыты нечетные зоны) 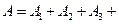 ….)
….)

a;b;m- расстояние от источника до поверхности сферы фронта волны; расстояние от сферы до точки наблюдения; номер зоны разбиения (первая: радиусом b+λ/2 и для m- ой: b+mλ/2).
Дифракция на круглом отверстии:
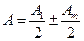 . + соответствует нечетным зонам. m – число открытых зон Френеля.
. + соответствует нечетным зонам. m – число открытых зон Френеля.
Дифракция на непрозрачном диске:
 , m – число закрытых зон Френеля.
, m – число закрытых зон Френеля.
Условие дифракционных максимумов от одной щели:
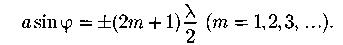
a;φ- ширина щели; угол распространения света, отсчитываемый от нормали к щели; m – порядок максимума (в центре максимум для m=0)
Условие дифракционных минимумов от одной щели:
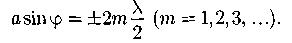
Условия главных максимумов дифракционной решетки:
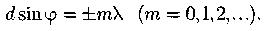
d- период дифракционной решетки. Центральный максимум соответствует m = 0.
Условие дополнительных минимумов дифракционной решетки:

N – полное число щелей решетки; 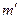 - может принимать все целочисленные значения, кроме указанных в скобках.
- может принимать все целочисленные значения, кроме указанных в скобках.
Формула Вульфа-Брэгга (направления, в которых будут наблюдаться дифракционные максимумы рентгеновских лучей при облучении кристалла. d - расстояние между кристаллографическими плоскостями):
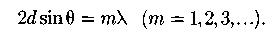
Разрешающая способность спектрального прибора:

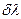 - минимальная разность длин волн двух соседних спектральных линий, при которой эти линии регистрируются раздельно.
- минимальная разность длин волн двух соседних спектральных линий, при которой эти линии регистрируются раздельно.
Разрешающая способность дифракционной решетки:
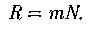
m;N- порядок спектра; число щелей дифракционной решетки.
Закон Бугера (поглощение света в веществе толщиной x):

α- коэффициент поглощения вещества зависящий также и от длины волны света). I - интенсивность света.
Продольный эффект Доплера (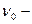 частота света, излучаемого источником):
частота света, излучаемого источником):
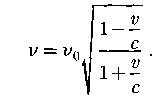
Поперечный эффект Доплера:
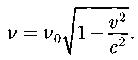
Степень поляризации:
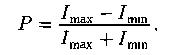
Закон Малюса
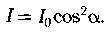
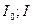 - интенсивность поляризованного света, падающего на второй кристалл, и вышедшего из него. α -угол между оптическими осями кристаллов.
- интенсивность поляризованного света, падающего на второй кристалл, и вышедшего из него. α -угол между оптическими осями кристаллов.
Закон Брюстера (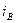 -угол падения, при котором отраженный луч является полностью плоскополяризованным перпендикулярно плоскости падения):
-угол падения, при котором отраженный луч является полностью плоскополяризованным перпендикулярно плоскости падения):
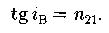
Оптическая разность хода в эффекте Керра (оптическая анизотропия под действием электрического поля):
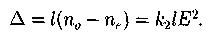
 - показатель преломления обыкновенного и необыкновенного лучей; постоянная, характеризующая вещество; путь лучей в среде; напряженность электрического поля.
- показатель преломления обыкновенного и необыкновенного лучей; постоянная, характеризующая вещество; путь лучей в среде; напряженность электрического поля.
Угол вращения плоскости поляризации в кристаллах:

d – расстояние, пройденное светом в среде; α- удельное вращение.
Угол вращения плоскости поляризации в растворах:
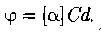
C – массовая концентрация оптически активного вещества в растворе.
Закон Кирхгофа для теплового излучения: Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности является для всех тел универсальной функцией частоты(длины волны) и температуры.

 - спектральная плотность энергетической светимости (мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины, Дж/
- спектральная плотность энергетической светимости (мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины, Дж/ 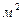 ); спектральная поглощательная способность (доля энергии, приносимая за единицу времени на единицу площади поверхности тела с частотами от ν до ν+d ν, поглощаемая телом, безразмерная).
); спектральная поглощательная способность (доля энергии, приносимая за единицу времени на единицу площади поверхности тела с частотами от ν до ν+d ν, поглощаемая телом, безразмерная).
Энергетическая светимость черного тела:

Закон Стефана-Больцмана:

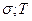 - постоянная Стефана Больцмана; термодинамическая температура.
- постоянная Стефана Больцмана; термодинамическая температура.
Закон смещения Вина:
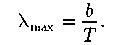
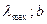 - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости; постоянная Вина.
- длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости; постоянная Вина.
Формула Рэлея – Джинса
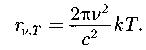
Формула Планка (h –постоянная Планка):
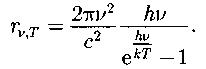
Уравнение Эйнштейна для внешнего фотоэффекта:
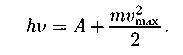
 -энергия поглощенного кванта света; работа выхода электрона; кинетическая энергия вылетевшего электрона.
-энергия поглощенного кванта света; работа выхода электрона; кинетическая энергия вылетевшего электрона.
Энергия фотона:
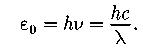
Импульс фотона:
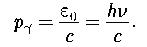
Давление света при его нормальном падении на поверхность:
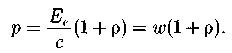
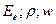 - энергия всех фотонов, падающая на единицу поверхности в единицу времени (энергетическая освещенность поверхности); коэффициент отражения света от поверхности; объемная плотность энергии излучения. Давление производят поглощенные и отраженные фотоны.
- энергия всех фотонов, падающая на единицу поверхности в единицу времени (энергетическая освещенность поверхности); коэффициент отражения света от поверхности; объемная плотность энергии излучения. Давление производят поглощенные и отраженные фотоны.
Изменение длины волны при эффекте Комптона (упругое рассеяние коротковолнового излучения на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны).
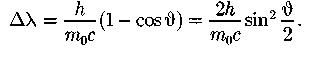
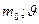 - масса электрона; угол, на который изменяется направление движения фотона после рассеяния.
- масса электрона; угол, на который изменяется направление движения фотона после рассеяния.
Атомная и ядерная физика
Обобщенная формула Бальмера (спектральные линии атома водорода):
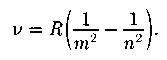
R - постоянная Ридберга; m=1,2,3,4,5,6 и определяет серию; n- принимает целочисленные значения, начиная с m+1. Серия Лаймана в ультрафиолетовой области: m=1, n=2,3…. Серия Бальмера в видимой области спектра m=2, n=3,4…. В инфракрасной области: серия Пашена, Брэкета, Пфунда, Хэмфри.
Первый постулат Бора (момент импульса электрона имеет дискретные (квантовые) значения, 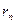 - радиус n -й орбиты:
- радиус n -й орбиты:
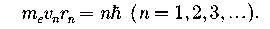
Второй постулат Бора (правило частот):
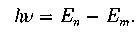
Энергия электрона в водородоподобном атоме:

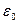 - диэлектрическая проницаемость вакуума.
- диэлектрическая проницаемость вакуума.
Длина волны де Бройля:
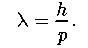
p - импульс.
Соотношение неопределенностей (микрочастица не может одновременно иметь и определенную координату и определенную одновременно соответствующую проекцию импульса; это же имеет место и для энергии и времени):
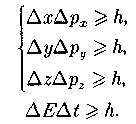
Вероятность нахождения частицы в элементе объемом dV (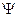 - волновая функция):
- волновая функция):
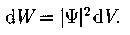
Условие нормировки вероятностей:
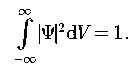
Общее уравнение Шредингера:
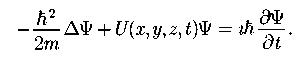
Уравнение Шредингера для стационарных состояний:
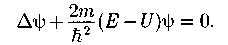
Волновая функция, описывающая состояние частицы в одномерной прямоугольной «потенциальной яме» с бесконечно высокими» стенками»:

Собственные значения энергии частицы в «потенциальной яме» с бесконечно высокими «стенками»:
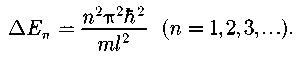
Коэффициент прозрачности прямоугольного потенциального барьера (отношение плотности потока прошедших частиц к плотности потока падающих):
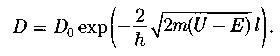
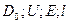 - постоянный множитель, который можно приравнять к единице; высота потенциального барьера; энергия частицы; ширина барьера.
- постоянный множитель, который можно приравнять к единице; высота потенциального барьера; энергия частицы; ширина барьера.
Энергия квантового осциллятора (квантовый осциллятор описывается уравнением Шредингера, где потенциальная энергия U равна потенциальной энергии гармонического осциллятора 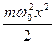 ):
):
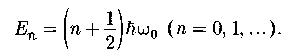
Уравнение Шредингера для электрона в атоме водорода (r - расстояние между электроном и ядром):
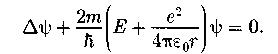
Нормированная волновая функция, отвечающая 1 s- состоянию электрона в атоме водорода (a -величина, совпадающая с первым боровским радиусом):

Закон Мозли (частоты рентгеновских спектров):
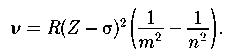
R;Z;σ – постоянная Ридберга; число протонов в ядре; постоянная экранировки; m = 1,2,3…( определяет рентгеновскую серию); n=m+1,…. (определяет отдельную линию соответствующей серии).
Распределение Бозе – Эйнштейна:
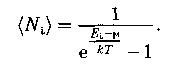
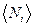 - среднее число бозонов (частиц с нулевым или целым спином) в квантовом состоянии с энергией
- среднее число бозонов (частиц с нулевым или целым спином) в квантовом состоянии с энергией 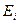 ;
; 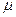 - химический потенциал (определяется только температурой и плотностью частиц).
- химический потенциал (определяется только температурой и плотностью частиц).
Распределение Ферми – Дирака (для фермионов – частиц с полуцелым спином):
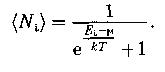
Уровень Ферми в собственном полупроводнике (уровень Ферми расположен в середине запрещенной зоны):

Удельная проводимость собственных полупроводников (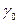 - постоянная для данного полупроводника). Проводимость растет с повышением температуры:
- постоянная для данного полупроводника). Проводимость растет с повышением температуры:
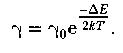
Правило Стокса для люминесцентного излучения (длина волны люминесцентного излучения всегда больше длины волны света, возбудившего его):
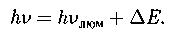
Ядерная физика
Радиус ядра:

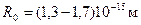 ; А – число нуклонов в ядре.
; А – число нуклонов в ядре.
Энергия связи нуклонов в ядре:

(Энергия связи всегда больше нуля, т.е. масса ядра всегда меньше чем суммарная масса нуклонов)
Дефект массы ядра:
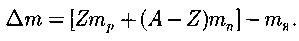
Магнетон Бора (единица магнитного момента электрона):

Ядерный магнетон (единица магнитного момента ядер):
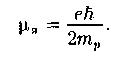
Закон радиоактивного распада:
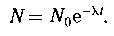

λ - постоянная радиоактивного распада (постоянная для данного радиоактивного вещества).
Период полураспада:

Среднее время жизни радиоактивного ядра:

Активность нуклида:
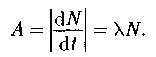
Правило смещения для α- распада:
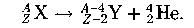
Правило смещения для 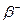 - распада:
- распада:
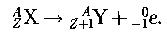
Правило смещения для  - распада:
- распада:

Символическая запись ядерной реакции:
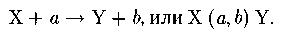
Справка: 






