Рассмотрим некоторые операции над автоматными функциями.
1. Отождествление двух или большего числа входных переменных. Еслифункция реализована схемой, то соответствующие этим переменам вершины будут просто отождествлены.
Если функция задана каноническими уравнениями, то при отождествлении каких-то переменных может уменьшиться вес автоматной функции.
Пример 10. Реализовать СФЭЗ автоматную функцию, получающуюся из заданной: 
отождествленными переменных  и
и  .
.
Положив 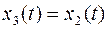 , получим систему уравнений
, получим систему уравнений 
Для определения веса этой функции надо построить дерево по системе канонических уравнений, вершины будем нумеровать двоичными кодами:  .
.
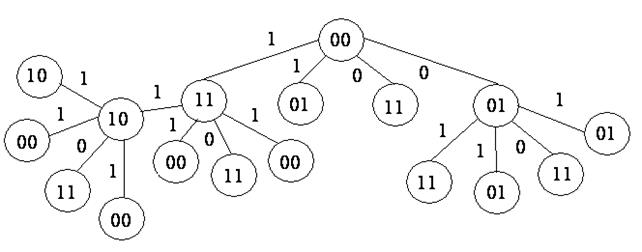 Рис. 19
Рис. 19
|
Когда строим дерево по заданной системе канонических уравнений, мы сразу получаем усеченное дерево. На графе видно, что состояние  , а состояние
, а состояние  . Поэтому вес функции равен 2, можно получить более простую систему уравнений и, следовательно, более простую СФЭЗ для ее реализации. Начальное состояние обозначим 0, другое 1, построим информативное дерево:
. Поэтому вес функции равен 2, можно получить более простую систему уравнений и, следовательно, более простую СФЭЗ для ее реализации. Начальное состояние обозначим 0, другое 1, построим информативное дерево:
 Рис. 20
Рис. 20
|
и каноническую таблицу

| 
| 
| 
| 
|
По канонической таблице получим простую систему уравнений: 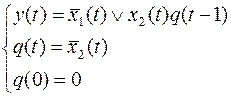
и СФЭЗ для нее реализации
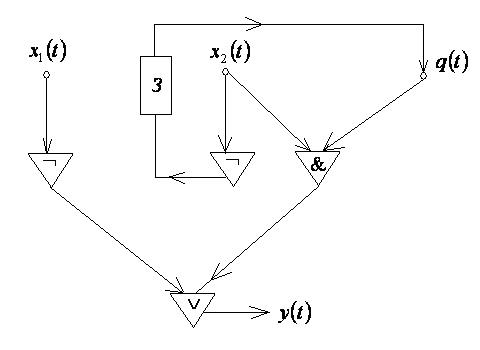 Рис. 21
Рис. 21
|
Введение обратной связи.
Определение. Выходная переменная  зависит от входной переменной
зависит от входной переменной  с запаздыванием, если для любого момента времени
с запаздыванием, если для любого момента времени  и для любых входных последовательностей
и для любых входных последовательностей

Если автоматная функция задана каноническими уравнениями, то в уравнении  переменная
переменная 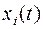 будет отсутствовать, так как для
будет отсутствовать, так как для  она является фиктивной.
она является фиктивной.
Если переменная  зависит от входной переменной
зависит от входной переменной 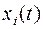 с запаздыванием, можно ввести обратную связь по переменным
с запаздыванием, можно ввести обратную связь по переменным  .
.
На рис. 22 схематично показано введение обратной, если автоматная функция реализована СФЭЗ. На схеме видно, что при такой процедуре уменьшается и число входных переменных, и выходных переменных, может уменьшиться вес функции.
 Рис. 22
Рис. 22
|
Если автоматная функция задана каноническими уравнениями, то во всех уравнениях вместо переменной 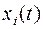 надо поставить функцию
надо поставить функцию  .
.
Пример 11. Построить канонические уравненияавтоматной функции, если в системе канонических уравнений:
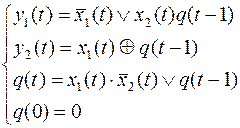
ввести обратную связь по переменным  .
.
 зависит
зависит  с запаздыванием, так как
с запаздыванием, так как 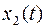 не входит в уравнение для
не входит в уравнение для 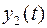 . Подставив его вместо
. Подставив его вместо 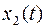 , получим
, получим

Уравнение можно упростить и привести систему к тривиальному виду
 или
или 
3. Суперпозиция двух автоматных функций 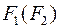
Если функция 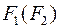 реализована СФЭЗ, то схематично она изображена на рис.23
реализована СФЭЗ, то схематично она изображена на рис.23
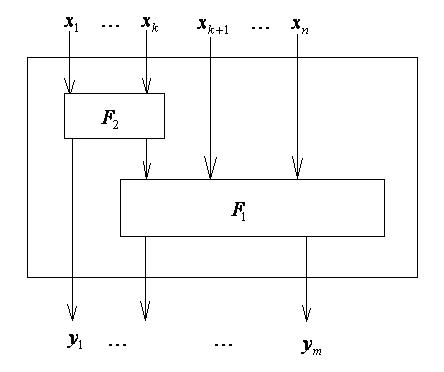 Рис. 23
Рис. 23
| Один или несколько выходов функции  поступают на входы поступают на входы  , ,  может иметь и свои входные переменные.
Если функция может иметь и свои входные переменные.
Если функция  имела вес имела вес  , функция , функция  имела вес имела вес 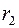 , то вес суперпозиции , то вес суперпозиции 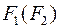 не превосходит не превосходит  . .
|
Мы ограничимся автоматными функциями с одним входом и причем у функции  входная переменная
входная переменная  выходная
выходная 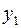 ,
,  выходная
выходная  для
для 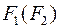 имеет вид:
имеет вид:

| Если  и и  заданы каноническими уравнениями, то вместо заданы каноническими уравнениями, то вместо  в систему для в систему для  подставим подставим  , и добавим к системе уравнений , и добавим к системе уравнений  уравнения задающие состояния автомата уравнения задающие состояния автомата  , вместе с начальными условиями. , вместе с начальными условиями.
|
Пример 12. Автоматные функции  и
и  заданы каноническими уравнениями:
заданы каноническими уравнениями:
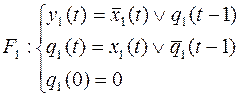
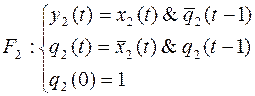
Построить канонические уравнения автоматной функции  и найти ее вес.
и найти ее вес.

Так как у нас осталось только одна входная переменная, положим  , аналогично:
, аналогично:  и упростим систему уравнений.
и упростим систему уравнений.

Построим информативное дерево, состояние в корне дерева (01)
 Рис. 24
Рис. 24
|
Эквивалентных состояний нет, поэтому вес дерева равен 4.
Рассмотрим еще один пример, который не связан с действиями с автоматными функциями.
Пример 13. Реализовать схемой из функциональных элементов с задержкой минимальной сложности в стандартном базисе, где суперпозицию функций  по переменным
по переменным 

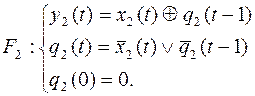
Канонические уравнения для суперпозиции  по указанным переменным получаются подстановкой выражения для
по указанным переменным получаются подстановкой выражения для  вместо переменной
вместо переменной 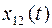 в канонические уравнения для
в канонические уравнения для  и добавляем к полученной системе уравнения
и добавляем к полученной системе уравнения  и начального условия
и начального условия 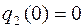 .
.
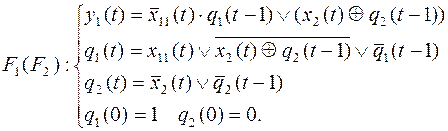
Перейдем к стандартному базису, по возможности, уменьшая сложность:

Вес полученной суперпозиции не превосходит четырех, но может быть и меньше. Для определения веса построим информативное дерево.
Душ, выходящие из каждой вершины, соответствуют наборам  : (00), (01), (10), (11).
: (00), (01), (10), (11).
 Рис.25
Рис.25
|
Вес функции равен трем, так как в дереве нет эквивалентных состояний, а состояние 00 отсутствует. Для описания трех состояний переменные 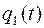 и
и  необходимы и упростить систему дальше не удается. Постоим СФЭЗ.
необходимы и упростить систему дальше не удается. Постоим СФЭЗ.
 Рис.26
Рис.26
|






