Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа. EK=(1/2)Nmv2=(3/2)RT для 1 моля N = Na, где Na — постоянная Авогадро. Nam = Mr, где Mr — молярная масса газа
Отсюда окончательно: v=корень из (3RT/Mr).
Средняя скорость: <v>= интеграл от0 до бесконечности от (v f(v)dv) <v>= корень из ((8KT)/ПИ*m)= корень из ((8RT)/ПИ*µ)
Наиболее Вероятная скорость: VP=корень из((2KT)/m)= корень из((2RT)/µ)
Максвелловское распределение молекул по их скоростям и энергиям
1. Возьмем идеальный газ. В результате столкновений молекул газа, их скорости все время изменяются, но в газе создается некоторое стационарное распределение молекул по их скоростям.
Пусть температура газа T = 300 K.
| Интервал скоростей | Доля молекул, имеющих скорости в заданном интервале |
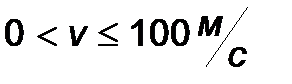
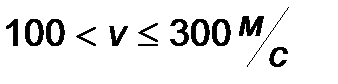
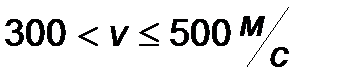
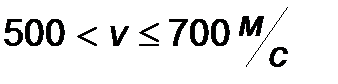
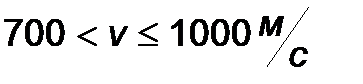
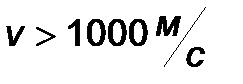
| 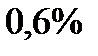

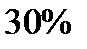
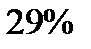

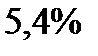
|
Эта таблица называется - распределением молекул по скоростям. Из этого распределения видно, что существует какая-то наиболее вероятная скорость.
2) Максвелл в 1860 г. получил формулу, которая описывает распределение молекул по скоростям:
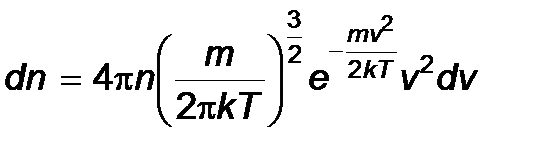 Максвелловское распределение молекул по их скоростям
Максвелловское распределение молекул по их скоростям
где n – число молекул в единице объема, dn – число молекул в единице объема, имеющих скорость в интервале от v до v + dv, m – масса молекулы, k – постоянная Больцмана, T – температура.
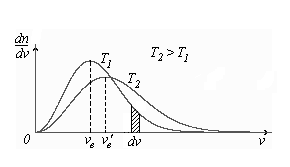
3) Построим кривые Максвелла для двух температур (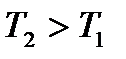 ).
).
|
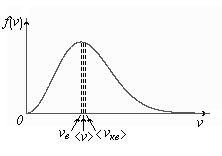
Физический смысл кривой Максвелла: dn/dv - число молекул, имеющих скорости в единичном интервале скоростей. Возьмем узкую полоску, которую можно считать прямоугольной. Ее площадь равна:(dn/dv)dv=dn. Тогда площадь под всей кривой Максвелла равна n.
4) Для того, чтобы придать вероятностный характер распределению Максвелла, введем новую функцию: dn/ndv=f(v) - функция распределения Максвелла молекул по их скоростям.
График этой функции имеет аналогичный вид, но теперь площадь под кривой f(v) равна 1. dn/n - имеет смысл вероятности того, что молекула имеет скорость в интервале от  до
до 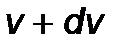 . Согласно определению функции
. Согласно определению функции  имеем dn/dn=f(v)dv, откуда видно, что f(v) - плотность вероятности того, что молекула имеет скорость в интервале от
имеем dn/dn=f(v)dv, откуда видно, что f(v) - плотность вероятности того, что молекула имеет скорость в интервале от  до
до 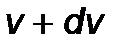 . Это очень важная величина в теории вероятности, позволяющая вычислять среднее значение любой физической величины, являющейся функцией скорости
. Это очень важная величина в теории вероятности, позволяющая вычислять среднее значение любой физической величины, являющейся функцией скорости  .
.
5) От распределения молекул по скоростям  можно перейти к распределению молекул по их кинетической энергии
можно перейти к распределению молекул по их кинетической энергии 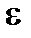 . Для этого надо в распределении молекул по скоростям выразить
. Для этого надо в распределении молекул по скоростям выразить  и
и 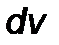 через
через 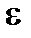 и
и 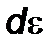 .
. 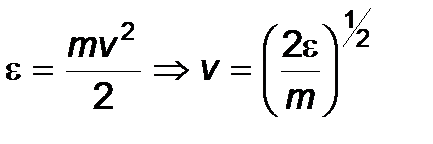 ,
,  .
.
Производя вычисления, получим
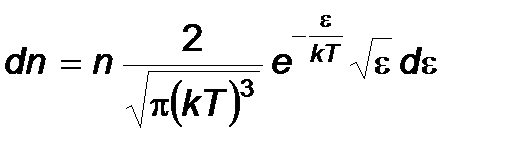 - Максвелловское расрпеделение молекул по их кинетическим энергиям.
- Максвелловское расрпеделение молекул по их кинетическим энергиям.
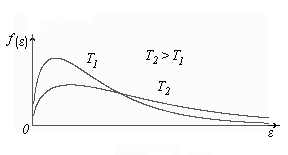
|
Аналогично вводится:
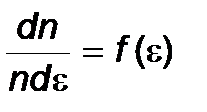 - функция распределения Максвелла молекул по их энергиям.
- функция распределения Максвелла молекул по их энергиям.
1) < vкв > - средняя квадратичная скорость молекул.
Для нахождения < vкв > можно воспользоваться выражением для средней кинетической энергии <e> поступательного движения молекул
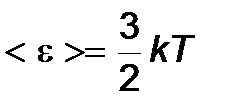 ,
, 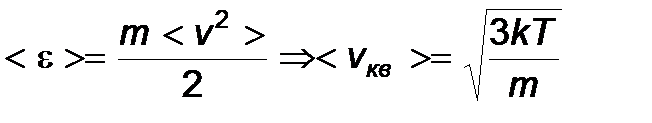 или вычислить интеграл
или вычислить интеграл
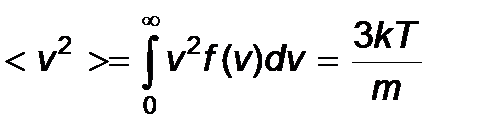
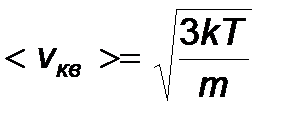 - средняя квадратичная скорость молекул
- средняя квадратичная скорость молекул
2) < v > - средняя арифметическая скорость молекул. 
3) 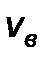 - наиболее вероятная скорость молекул
- наиболее вероятная скорость молекул
Это скорость молекул, при которой функция распределения  имеет максимум. Возьмем производную от
имеет максимум. Возьмем производную от  , и приравняв ее нулю, получим уравнение для нахождения
, и приравняв ее нулю, получим уравнение для нахождения 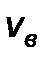 :
:
|
(df(vв))dv=0 df, -(mvв3/kT)+2vв=0, vв2=2kT/m,
 - наиболее вероятная скорость молекул
- наиболее вероятная скорость молекул
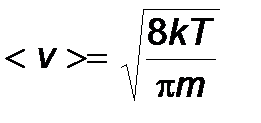 - средняя арифметическая скорость молекул
- средняя арифметическая скорость молекул






