Наземные комплексные испытания СВВП с гонкой двигателя необходимо производить при различных ею положениях относительно земли. Как следует из условий эксплуатации, описанных во вводном разделе, на выходные параметры (Мх. Му, Mz) действуют следующие основные факторы: угол наклона по крену γ с диапазоном от —10° до +10°; по тангажу— θ с диапазоном от —10° до +10°; высота от нижней поверхности фюзеляжа в точке приложения равнодействующей от трех маршевых двигателей до земли h, [м] с диапазоном от 0,5 м до 2,5 м; вес самолета, соответствующий определенным количествам топлива V в процентах от полного объема баков.
Для полной ясности исследуемого процесса разработаем оперативную концептуальную модель испытаний (рис. 7). Модель содержит как основные, так и второстепенные факторы. Студентам необходимо в процессе последующего статистического анализа произвести ранжирование основных факторов с выделением главного и второстепенных в соответствии с разделом 1.2.4.
Поскольку любой эксперимент должен быть оснащен в соответствии с установленными параметрами определенными средствами отображения информации, построим информационную модель наземных испытаний СВВП (рис. 8). В ней отражаются методы и средства контроля за ходом исследуемого процесса выделенным выходным параметрам процесса. В приведенной модели студенты должны раскрыть принципиальное содержание каждого метода по замеру соответствующего параметра.
Обе модели взаимосвязаны, информационная модель в основном верно отражает физический процесс испытаний (эксплуатации), который абстрагирован концептуальной моделью.
Следовательно, результаты испытаний достоверно отражают основные зависимости в ходе испытаний и степень их аппроксимации будет определяться характеристиками наземного оборудования в комплексе с КЗА.
Таким образом основные составляющие разработанных моделей должны быть включены в ТУ на проведение данных испытаний и в ТЗ на проектирование соответствующего стенда.
Диапазоны основных факторов удобно разбить на 4 равных интервала, т. е. па 5 уровней. Угол γ (крен): —10°; —5°; 0°; +5°; +10°; угол θ (тангаж): —10°; —5°; 0°; +5°; +10°; высота h, [м]: 0,5; 1,0; 1,5; 2,0; 2,5; вес СВВП, соответственно количеству топлива V, (%): 20; 40; 60; 80; 100. Такое разделение по уровням удобно также и с точки зрения планирования испытаний по методу комбинационных квадратов (см. 2.1).
Порядок проведения испытаний. Предположим, что для наземных испытаний осуществимы все сочетания уровней основных факторов. Тогда испытания возможно провести по последовательной программе, определяемой последовательным выгоранием топлива, с рандомизированным контролем по точкам, включенным в план комбинационного квадрата. Причем прокачка уровней всех остальных факторов; кроме массы топлива, может иметь и случайный характер, т. е. в данном случае эксперимент смешанный, последовательно-рандомизированный. Разработку плана произведем в разделе анализа результатов испытаний, поскольку там же будем проводить в соответствии с полученными данными определение эмпирических зависимостей по методу случайного баланса, заложенного в основе построения комбинационных квадратов.
Анализ. Оптимизация испытаний связана с уменьшением количества контрольных замеров. Если испытания проводить по методу ПФЭ (см. раздел 1.1.1.), то их количество составит 5*5*5*5 = 54 = 625 по каждому выходному параметру. Их в нашем опыте три. Следовательно, число замеров 625*3 = 1875. Применив метод случайного баланса с комбинационными квадратами, общее число замеров сокращается в 25 раз и составит 75.
Построение комбинационного квадрата (КК) можно, например, произвести следующим образом. Построим вначале, образно говоря, «каркас» КК (табл. 19) для одного выходного параметра, например,Мх (для других квадрат будет тот же, отличие только в значениях выходного параметра в клетках квадрата).
[1] Удобней проводить подобные испытания следующим образом: один из факторов, высоту, установить на одном уровне, тем более, что это связано с переналаживанием опорных стоек, углы у и 0 менять в соответствии с планом по мере последовательного выгорания топлива.
Теперь необходимо выбрать 25 клеток, по одной в каждом среднем квадрате, которые будут обозначать контролируемые сочетания уровней основных факторов, т. е. выбранные случайным образом значения Мх, (Н*м). Располагаться выбранные клетки должны так, чтобы па каждой строке и в каждом столбце было по одной клетке, а, следовательно, и в каждом среднем квадрате 5*5. Это возможно в нашем случае, поскольку число уровней каждого фактора одинаково. Для этой цели построим средний квадрат отдельно (табл. 20). Нумеруем по порядку все его клетки и по определенному принципу переносим их в большой квадрат па табл. 19. Перенос начнем с центральной клетки 13, которую очертим в центральном среднем квадрате КК. На цифровые обозначения пока обращать внимание не нужно. В соседние верхний и нижний квадраты относительно центрального перенесем клетки 7, 13, в правый и левый — 9 и 17. В самый верхний и самый нижний средние квадраты занесем клетки 25 и 1, а в правый и левый—21 и 5. Осталось занести клетки в 4 группы средних квадратов по 4 в каждой в углах КК в табл. 19. Заполним левую вертикаль, во второй и четвертый квадраты — клетки 16 и 22 (на табл. 20 все подобные комбинации клеток отмечаем стрелками), в первый и 5 квадраты — клетки 8 и 14. Также занесем в правую 5-ую вертикаль клетки 18 и 12, 4 и 10. Клетки 24 и 20 заносим в квадраты 2 и 4 нижней горизонтали, клетки 6 и 2—в те же квадраты верхней горизонтали. Оставшиеся клетки 3 и 23; 11 и 15 заносим в соседние квадраты по диагонали от среднего.
Допустим в процессе испытаний СВВП были получены по параметру Мг следующие данные, проставленные в выбранных клетках КК на табл. 19. Произведем усреднения результатов по парам факторов: h—V; γ—θ в табл. 21 и табл. 22.
Таблица 21
| h V | Σ | ср. | |||||
| Σ | |||||||
| ср. |
Таблица 22
| γ θ | Σ | ср. | |||||
| Σ | |||||||
| ср. |
Представим первые усреднения в графической форме на рис. 8. Анализируя графики, предположим, что зависимость F(h) линейная. Она наиболее сильно влияет на функцию отклика М х, поэтому, применив метод случайного баланса и исключив влияние h, упрощаем определение других зависимостей. Из графика F(h) =2+ 15ĥ, где ĥ — нормированное обозначение фактора по номеру уровня. Из формулы видно, что при переходе с уровня на уровень Мх изменяется на 15 единиц. Следовательно, чтобы нейтрализовать фактор h, нужно в табл. 19 из значений Мх, соответствующих 4 и 5 уровню h, вычесть величину (ĥ—3)15 — для ĥ = 4, ĥ = 5. Для значений Мх, соответствующих 1 и 2 уровню h—прибавить ту же величину, тогда после пересчета Мх =f(h) будет постоянной и величина ее соответствовать ĥ = 3. Значения Мх по данному пересчету запишем в скобках в табл. 19 рядом с занятыми исходными данными клетками. Далее перепишем их в табл. 23 для пары факторов θ— γ.
Усредненные данные по θ— γ опять не дают явных зависимостей от указанных факторов. Следовательно, предположение о линейной зависимости результатов от фактора h и, если произвести пересчет, то и от фактора V неточно. Необходимо проверить более сложную зависимость от данных факторов. Предположим, что Мх зависит от произведения h*V (можно рассматривать такжеh/V; h+V). Расчеты сведем в табл. 24.
Заполнение ее производилось следующим образом.
Из табл. 21 взяли первую горизонталь, в которой при ĥ-Ṽ = 1, Мх = F = 10, при ĥ*Ṽ=2, F=13 и т. д. Причем контролировалось, что, например, ĥ*Ṽ=4 (т. е. ĥ = 4, Ṽ= 1; ĥ = 2 и ĥ= 1, Ṽ = 1) соответствует 3 значения F (19, 19, 37), a ĥ*Ṽ=8 (т.е. ĥ*Ṽ = 4*2 = 8 и ĥ*Ṽ = 2 *4 = 8) соответствует 2 значения F (59 и 29) и т. д.
Таблица 23
| γ θ | Σ | ср. | |||||
| Σ | |||||||
| ср. |
По данным табл. 24 построим график F=f(h*V), по которому определяем, что данная корреляционная зависимость может быть аппроксимирована прямой линией с угловым коэффициентом 5 (рис. 9). Чтобы нейтрализовать влияние произведения h*V на параметр F, пересчитаем первоначальные данные (в очерченных клетках табл. 19), вычитая соответствующую величину 5 ĥ*Ṽ из определенных ей в табл. 24 значений F. Например, из значений F 38 и 14, соответствующих ĥ*Ṽ = 5 в табл. 24, нужно вычесть 5*5 = 25. Полученные величины 38—25=13 и 14—25 = —11 проставляем без скобок рядом с первоначальными данными в очерченных клетках в табл. 19. Здесь же суммируем их и производим осреднение по факторам h и V. Влияние фактора h оказалось практически компенсированным, но влияние V сохранилось. Получается, что сохранившаяся корреляционная зависимость линейна с угловым коэффициентом 3 на уменьшение. Поэтому, чтобы точнее нейтрализовать влияние фактора V, нужно произвести повторный пересчет результатов, добавляя к ним величину 3V. Получаемые данные запишем во вновь построенном КК таблицы 25.
Таблица 24
| ĥ*Ṽ | Мх = F | ||
Произведем группировку результатов по факторам θ и γ в таблицу 26, откуда видно, что средние значения пересчитанной функции, обозначим ее F2, по фактору Θ растут примерно, как Ǿ2. Это наглядно представлено на рис. 10.
По фактору γ средние значения изменяются в соответствии со следующей эмпирической зависимостью F2(γ)=9—Зỹ. Угловой коэффициент, равный 3, определен по возрастанию F2 на 3 единицы на 1 уровень. Константа а = 9 определена так. Поскольку средние значения по фактору в табл. 26 просчитаны с учетом фактора θ, то нужно из этих значений вычесть усредненное значение F2, соответствующее третьему (среднему) уровню θ, т. е. 11. Тогда первому уровню γ соответствует
, а константа уравнения определяется при Y=0, т. е. а=6 + 3 = 9
Рис. 9. Корреляционная связь функций F и произведения факторов  . 
|
Теперь из данных в клетках табл. 25 вычтем величины 9—Зу+Ɵ2. Например, для среднего квадрата в левом верхнем углу КК: 8 - 9 + 3*4-32=2, что и записано рядом с очерченной клеткой и т. д. Анализируя новые данные можно заметить, что значения вновь пересчитанной функции 
по факторам 0 и h колеблются около нуля (что можно проследить от уровня к уровню), а по факторам V и у составляют некоторую закономерность. Составим по данной паре факторов таблицу 27. Полученная симметричная квадратная матрица
описывается формулой = (
—3) (3—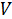 
).
Для исследуемой совокупности числовых значений эта зависимость завершает цепь выявленных- закономерностей. Складывая их, найдем:
F=5 
—3ng w:val="EN-US"/></w:rPr></m:ctrlPr></m:accPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>V</m:t></m:r></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 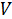+9-Зу+Ɵ2 + ( - 3) (3 - ) 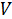или
F— (5 
— ) ng w:val="EN-US"/></w:rPr></m:ctrlPr></m:accPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>V</m:t></m:r></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> +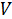 
2
| Таблица 25 |
| -4 | -2 | |||||||||||||||||||||||
| -1 | ||||||||||||||||||||||||
| -1 | ||||||||||||||||||||||||
| -2 | ||||||||||||||||||||||||
| -5 | ||||||||||||||||||||||||
| -2 | -4 | |||||||||||||||||||||||
| -1 | ||||||||||||||||||||||||
| -2 | -4 | |||||||||||||||||||||||
Y
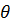
| ср | 
| 
| |||||
| ||||||||
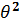
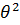
| Ср |
Таблица 27
| V | Y | ∑ | |||||
| -1 | -2 | ||||||
| -2 | -1 | ||||||
| -1 | -2 | ||||||
| -2 | -4 | ||||||
| ∑ |
Таким образом установлена общая эмпирическая зависимость М х от всех факторов, состоящая из суммы произведений функций от h и V и степенной функции от 0.
При выполнении задания студенты должны построить графики как общей, так и составляющих эмпирических зависимостей.
2.3. Тема 3. Планирование частных летных испытаний
Самолета
Летные испытания относятся к высшей ступени иерархии испытаний летательных аппаратов (см. рис. 1). Они, как правило, многоцелевые, т. е. в процессе их проведения решается много задач различного характера. Можно указать следующие основные частные цели программы летных испытаний: а) проверка реализуемости принципов, принятых при проектировании, и правильности функционирования системы; б) проверка адекватности разрабатываемой математической модели реальной системы; в) контроль работоспособности системы; г) определение надежности систем.
Постановка задачи. Мы рассмотрим задачу планирования частной программы летных испытаний, определяющей последовательность действий при исследовании процесса нагрева хвостовой части фюзеляжа (ХЧФ) самолета. Проведение такого исследования необходимо для установления зависимостей температуры конструктивных элементов ХЧФ (обшивки, защитного теплового экрана) от температуры выхлопной газовой струи двигателя типа ТРД от эксплуатационных факторов.
Выходным контролируемым параметром, следовательно, является температура соответствующих элементов самолета, измеряемая термопарами- Поскольку термопары, установленные в экране и обшивке, имеют большую тепловую инерционность вследствие большой массы обшивки или экрана, в которую они встроены, то удобнее взять за контрольную точку термопару, установленную в набегающем потоке газов возможно дальше от корпуса в так называемых «гребенках» (рис. 11). Располагают гребенки на корпусе ХЧФ так, чтобы они были направлены к оси струи двигателя. Этим поток газов из двигателя как бы препарируется по своей глубине термопарами гребенок.
Двигатели самолета располагаются под крыльями вблизи фюзеляжа, вследствие чего струя выхлопа «лижет» ХЧФ. Предполагаем, что интенсивность ее воздействия определяется режимом работы двигателя. В то же время существенную роль играет скорость полета или число M= v/a т. е. величина аэродинамического нагрева. Играют роль в нагреве ХЧФ и другие эксплуатационные и конструктивные факторы. До разработки технологического процесса необходимо провести их анализ и ранжирование, составив концептуальную модель данного физического процесса.
Далее определить возможности информационной модели бортового контрольно-измерительного комплекса в представлении достоверных данных об исследуемом процессе нагрева в полете.
Н.П
|
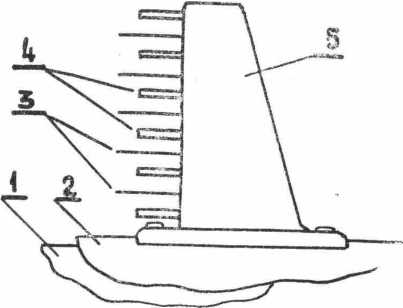
| Рис. 11. Схема гребенки. 1. Обшивка самолета; 2. Тепловой экран; 3. Стека- тель электрозарядов; 4. Защитные трубки с термопарами; 5. Гребенка. |
Анализируя полученные данные с помощью статистических комплексов Длина (СКД), определим достоверность влияния выбранных основных факторов на выходной параметр (отклик) процесса, а также графическую форму основных эмпирических зависимостей. Произведенные действия позволяют разработать частную оптимальную последовательность летных испытаний для контроля нагрева ХЧФ за более короткий цикл.
Определение состава факторов, влияющих на тепловой режим ХЧФ. Применительно к испытаниям, относящимся к активно-пассивным и пассивным экспериментам (например, огневые, летные, баллистические), возможно применение математического моделирования, исходным и практически обязательным этапом которого будет построение концептуальных моделей в процессе изучения статистических данных о фактор ном составе испытаний и контролируемых (выходных) параметрах системы. Такой подход применяется, поскольку структура исследуемых процессов испытаний, как правило, мало изучена, не ясна, или не поддается аналитическому описанию.
Принцип построения собственно математической модели будет определяться: наличием априорной информации, степенью понимания физических процессов испытаний, знанием и оценкой предполагаемых функциональных связей между элементами системы и т. д.
На рис. 12 представлена концептуальная модель физического процесса нагрева хвостовой части фюзеляжа (ХЧФ) самолета.
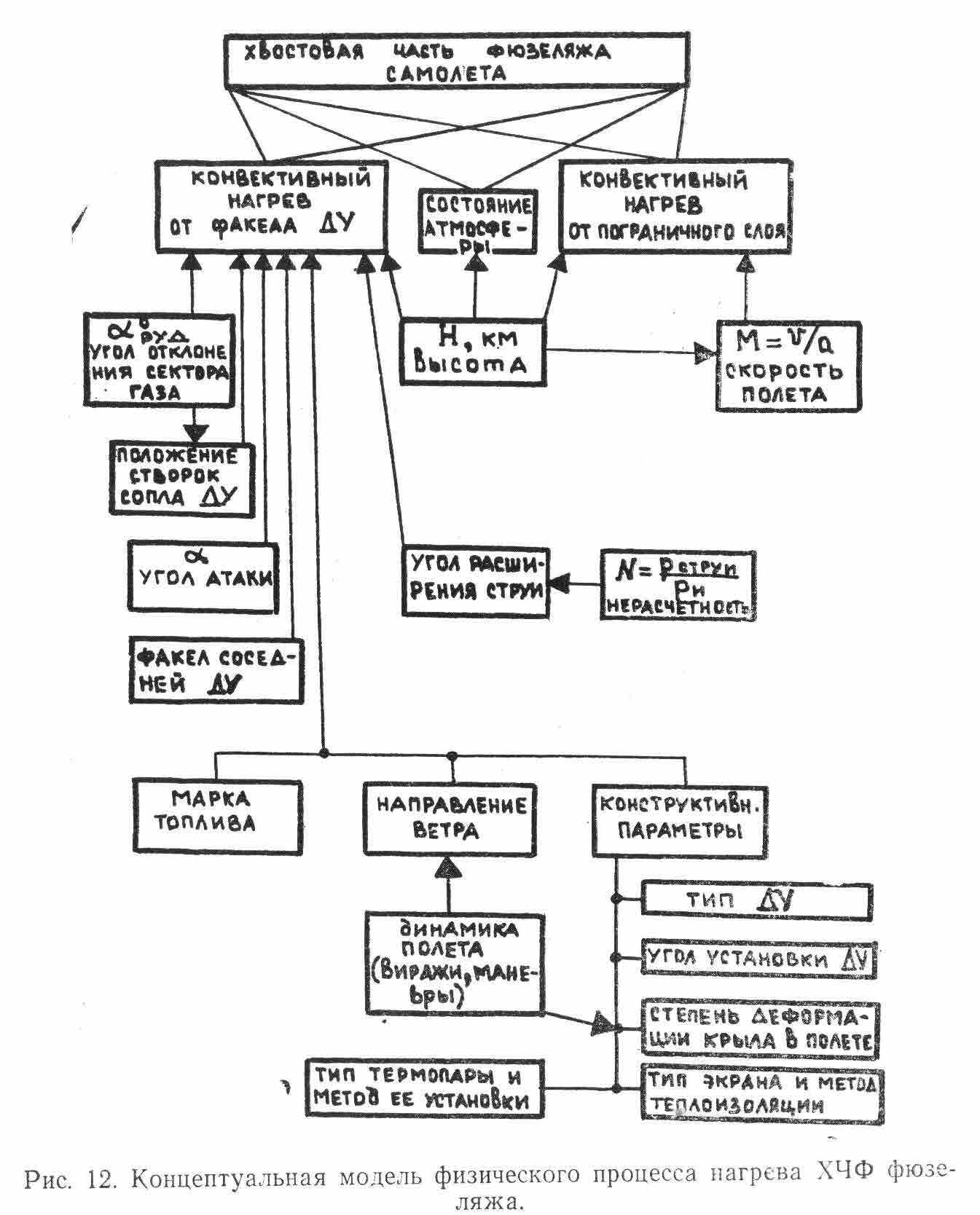
Модель включает большинство известных факторов различной природы, действующих на ХЧФ и выявленных на первой стадии исследования методом экспертного опроса.
В соответствии с экспертными оценками и эмпирическими предпосылками, основанными на результатах предыдущих летных испытаний, представленный состав факторов можно разбить на следующие группы, воспользовавшись классификацией Длина А. М. [9].
Структура классификации содержит такие группы факторов: основные, выключаемые, присоединившиеся и прочие.
Основные делятся на главный, дополнительные и вспомогательные. Предполагается, что главный фактор, влияющий на нагрев обшивки ХЧФ,—аруд — угол установки сектора газа ДУ (он определяет и соответственное положение створок сопла), т. е, режим работы двигателей. При а руд = const основную роль в тепловом режиме ХЧФ с большой достоверностью играет число Маха—М (при этом необходимо контролировать корреляцию а—скорости звука и высоты полета, 2 также М и а руд), определяющее величину аэродинамического нагрева обшивки. Поэтому число М назовем дополнительным фактором.
Заметное влияние оказывают, вероятно, на процесс нагрева высота полета Н (км) и угол атаки самолета а, [град], но для исследования они малосущественны, особенно при испытании на крейсерском режиме полета. Эти 2 фактора отнесем к вспомогательным. При дальнейшем анализе будем принимать во внимание из них только высоту полета —Я, поскольку угол атаки “а согласно экспертным оценкам изменяется в процессе полета незначительно, как в горизонтальном полете, так и при выполнении виражей, маневров, к тому же имеются сложности в достоверном измерении а в процессе полета.
К вспомогательным возможно отнести также влияние факелов (струй) других двигательных установок. Если примем за основной факел — ДУ № 2 (левый борт ХЧФ), то вспомогательным будет ДУ № 1.
К выключаемым факторам относится влияние состояния атмосферы в различные дни и даже в разное время суток, т. е. температуры воздуха (окружающей среды). Ее влияние можно уменьшить приведением фактической температуры окружающей среды к стандартным условиям MCA:
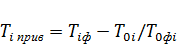(32)
где Т i ф— фактическая температура /-го замера, [°К];
T о фi —фактическая температура пограничного слоя в данной точке, [°К];
Т Нфi—фактическая температура атмосферы на соответствующей высоте экспериментального полета, [°К];
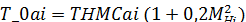
Полученные значения Т ПриВ каждому замеру заносятся в статистический комплекс для последующей обработки.
К выключаемым отнесем также конструктивные параметры, которые для одной модели самолета практически постоянны, а для других их влияние может быть устранено путем введения дополнительных коэффициентов пересчета; и марку топлива, которая в данном исследовании полагается неизменной по всем заправкам.
К присоединившимся факторам, вероятно, относятся: —
нерасчетность течения струи N=Pстр/Pк (коррелированная
высотой Н и, следовательно, косвенно учитываемая фактором Я в исследовании);
— направление ветра, определяющего скольжение самолета и, следовательно, более интенсивный нагрев левого или правого бортов ХЧФ.
Присоединившиеся факторы сложно контролировать, но их влияние нужно учитывать в конечном анализе процесса.
Как упоминалось выше, в исследовании приняты объектом контрольные точки левого борта ХЧФ. Поэтому для них влияние факелов правых двигателей ДУ № 3 и ДУ № 4 можно отнести к прочим факторам, их воздействие можно считать случайным.
Установим следующие уровни факторов на основе опроса экспертов и имеющихся априорных данных:
— для а: 1) 90°—94°, 2) 95°—99°, 3) 100°—106°, 4) 107°—114°, 5) 115°—118°;
— для числа М: 1) 1,50—1,69, 2) 1,70—1,79, 3) 1,80—1,84, 4) 1,85—1,89, 5) 1,90—1,94, 6) 1,95—1,99, 7) 2,00—2,12;
— для высоты Н: 1) 13,5—15,5, 2) 15,6—17,0, 3) 17,1—19,5. Установленные уровни могут быть изменены, например,
после первого расчета статистического комплекса, показавшего недостаточную сходимость результатов и предпосылок. Необходимо иметь в оптимальном варианте по 7 или 5 уровней каждого фактора, тогда статистические расчеты симметричных комплексов упрощаются и дают более достоверные результаты (см. 1.1.1).
Порядок проведения испытаний. Сразу возможно предположить, что в статистическом комплексе будут пустые клетки, вследствие невозможности воспроизведения в реальном полете отдельных сочетаний основных факторов. Это определяется тактико-техническими данными (ТТД) самолета. Следовательно,при разработке последовательности действий пилота в процессе летных испытаний необходимо учесть данные ограничения. Летный эксперимент рандомизирован, поскольку различные сочетания уровней основных факторов воспроизводятся случайно в зависимости от режима полета и зависят еще от множества второстепенных факторов, т. е. такой эксперимент фактически еще и невоспроизводим (см. 1.1.3).
Анализ результатов испытаний
Для анализа результатов по неполному сочетанию уровней выбираем СКД с незаполненными клетками (1.1.1). Чтобы избегать влияния невоспроизводимых факторов среды по разным системам, проанализируем данные по одному испататель- ному полету. Для этого занесем их в СКД таблицу 28.
| H | 
| M | |||||||
| H |
| M | |||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
| |||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
| |||||||||||||||||||||||
|
|
| |||||||||||||||||||||
|
| ||||||||||||||||||||||
| |||||||||||||||||||||||
|
| ||||||||||||||||||||||
Произведем расчет исходных статистических величин и сведем их в табл. 29. В каждой клетке полученной таблицы в соответствии в данными в табл. 28 записаны: в левом верхнем углу —сумма значений температур для данного сочетания уровней факторов 
в правом верхнем углу число экспе- риментальных данных — т\ в левом нижнем углу — средняя
величина значении в данной клетке -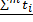 
; в правом ншк
нем углу—величина 
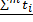=- Например, для
сочетаний уровней Н=1; М= 1; a=3 запишем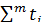 
= 38+
+ 45 + 70= 153; m = 3; R131=153^2/3 = 7803.
Для всего СКД число значений tt N= 37, количество групп значений (количество занятых клеток) по отдельным сочетаниям уровней факторов г—26, тогда число степеней свободы между группами 
=r—1 = 26—1 = 25 и число степеней свободы колеблемости значений температур под воздействием неучтенных факторов 
—N—r=37—26=11.
Для всего комплекса определяем величину
R, = 
= 3376^2/37 = 308037.
Квадрат меры варьирования (дисперсионная характеристика процесса), характеризующий колеблемость t,• под влиянием воздействия всех трех факторов а, М и Н:
= 
=1376; 
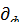≈37,1
Квадрат меры варьирования tt под влиянием
неучтенных факторов:
= 
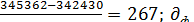≈16,3
Тогда критерий Фишера т. е. достоверность влияния трех факторов на температуру ХЧФ:
Ɵ= 
=1376/256=5,15
Для k1=25 и k2 = 11 при 99% вероятности подтверждения гипотезы о влиянии факторов критерий Фишера Ɵ1 = 4,27 (см. приложение 2). Величина Ɵ = 5,15, большая Ɵ1 ==4,27 показывает, что влияние трех основных факторов на нагрев ХФЧ подтверждается с вероятностью 99%.
Эту гипотезу возможно проверить также по величине совокупного коэффициента детерминаций
η3=(r-1) 
ф2/(r-1) 
ф2+(N-r)б02=25*1376/(25*1376+11*267)=0,92
Это означает, что три основных фактора а, М, Н оказали влияние на процесс нагрева ХЧФ предположительно на 92%, а 8% влияния приходится на долю неучтенных факторов.
Отсюда коэффициент множественной (совокупной) корреляции η= 
=0,96
Показательной оценкой распределений случайных величин служит пограничное значение г|о [9], регистрирующее границу между наличием и отсутствием закономерной связи между воздействующими факторами и температурой ХЧФ:
η0=(r-1)/(N-1)= 
=0,69
Полученный ранее показатель 'корреляционной связи η2= 0,92 превышает η02 на величину разницы η2— η0 2=0,92—0,69 = 0,23. Эта разность достигает своего максимального значения при η2=1, т. е. 1— η2= 1,0—0,69=0,31.
Сравнивая (η2— 
) с (1- ),. получим исправленную меру связи факторов а, М, Н с выходным параметром t1
η2испр = (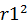
- 
)/(1- )= 
=0,74
Этот показатель можно получить также по формуле:
η2 =(r-1)( ф2- 02).((r-1) ф2+(N-r) ф2)=(26-1)(1376-267)/(26-1)1376+(37-26)*267=0,74
Полученная величина η2 = 0,74 также характеризует достаточно плотную корреляцию fj от основных факторов.
Следующий этап корреляционного ана шза — определение ранга основных факторов, т. е. выделение по тесноте связи с откликом. Расчет проводим по формулам, предложенным выше. Для удобства сведем данные табл. 28 в табл. 30, построенную по 2 факторам М и а. По априорным данным влияние высоты на отклик незначительно, и эту часть расчета проведем в последнюю очередь.
| M/а | т | ||||||||
| 108 84 82 | |||||||||
| 38 70 4:5 | |||||||||
| 107 112 110 118 | |||||||||
| т |
Предположим, что главный фактор нагрева ХЧФ — число М, и исследуем его корреляционные характеристики.
Первоначально определим достоверность влияния
числа ЙЕ на отклик — температуру контрольной термопары ХЧФ. Для этого в табл. 30 просчитаем суммы столбцов я занесем в строку «2», а также в строку «яг» занесем количество значений t i в каждом столбце. Число таких групп значений tt rм =7 определилось в данном случае для двухфакторной матрицы по числу уровней исследуемого фактора. Общее количество t,N=37 (N=Еmi;). Тогда для каждой группы т. е. для каждого столбца:
Rm1= 
=233^2/4=13572;Rm2=227^2/4=12882
Rm3=572^2/6=54531;Rm4=312^2/4=24336;
Rm5=1120^2/10=125440;Rm6=165^2/2=13613;
Rm7=740/7=80143
Д
