Если функция y = f(x) дифференцируема в точке х, т.е. имеет в этой точке конечную производную y′, то 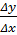 = y′ + α, где α →0 при
= y′ + α, где α →0 при 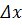 →0
→0
Отсюда:
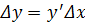 +α
+α 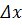
Главная часть y′ 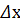 приращения функции, линейная относительно
приращения функции, линейная относительно  называется дифференциалом функции и обозначается dy.
называется дифференциалом функции и обозначается dy.
Учитывая, что dx= 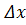 будем иметь
будем иметь
dy = y′dx
При достаточно малом dx= 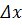 приращение функции равно ее дифференциалу.
приращение функции равно ее дифференциалу.
Сформулируем свойство инвариантности дифференциала:
dy = f ′x(x) dx = f ′u(u) du
Дифференциал функции равен произведению производной этой функции на дифференциал аргумента, где аргумент может быть и независимой переменной и функцией от другой независимой переменной.
Процесс отыскания дифференциала, как и операция нахождения производной, называется дифференцированием.
158. Найти дифференциал dy функции:
y = 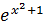
Решение. Исходя из определения дифференциала, имеем:
dy = y dx = 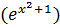 ′dx =
′dx = 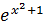 2x dx
2x dx
Данную функцию можно представить так: y = eu, где u = x2+1. Тогда будем иметь:
dy = eudu = 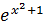 d(x2 + 1) =
d(x2 + 1) = 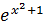 2x dx
2x dx
159. Найти дифференциал dy функции:
y = arctg esin 3x
Решение. Найдем производную y′, пользуясь правилом дифференцирования сложной функции:
y′ = 1/(1+(esin 3x )^2) esin 3x ∙ cos 3x ∙ 3
Тогда:
dy = 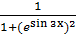 esin 3x ∙ cos 3x ∙ 3 dx
esin 3x ∙ cos 3x ∙ 3 dx
Дифференциал применяется для приближенных вычислений. Из формулы
f(x+Δx) ≈ f(x) + y′Δx (1), получаем
f(x2) ≈ f(x1)+ f(x1)(x2 – x1) (2)
160. Найти приближенное значение функции
f(x) = 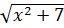
При х = 3,02 исходя из ее точного значения при х = 3.
Решение. Положим x1= 3 x2 = 3,02
Применяя приближенное равенство (2), будем иметь:
f(3.02)=  ≈
≈  + f ′(3)
+ f ′(3)  (3,02 - 3) = 4 + f ′(3)
(3,02 - 3) = 4 + f ′(3)  0,02
0,02
Чтобы найти f ′(3), надо предварительно данную функцию продиф-ференцировать и затем найти численное значение производной при х = 3
f ′(x) = 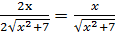 , f ′(3) =
, f ′(3) = 
Таким образом:  ≈ 4+
≈ 4+ 
 0,02 = 4,015
0,02 = 4,015
161. Найти приближенное значение величины tg 470
Решение. Рассмотрим функцию y = tg x. Известно, что tg 450=1. Поэтому удобно положить x1 = 450 и x2 = 470.
Чтобы воспользоваться приближенным равенством (2), необходимо предварительно найти значение функции y = tg x и ее производной y′ = 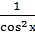 при x1 = 450 =
при x1 = 450 =  y
y 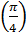 = 1 y′
= 1 y′ 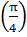 = 2
= 2
Разность: x2 – x1 надо выразить в радианной мере
x2 – x1 = 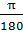 47 -
47 -  =
= 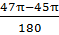 =
= 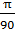 = 0,035
= 0,035
Следовательно: tg 470 ≈ 1+2  0,035 = 1,070
0,035 = 1,070
Вычислить приближенно:
162. y = 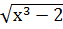 при х = 3,02 163. y =
при х = 3,02 163. y = 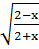 при х=0,02
при х=0,02
164. y = 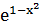 при х = 1,05 165. cos 610
при х = 1,05 165. cos 610
166. tg 440 167. e0.2
168. 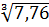 169. arctg 1,05
169. arctg 1,05
170. arcsin 0,54 171. ln 11
172. cos 1510
173. Доказать формулу 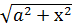 ≈ a +
≈ a + 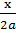 (
(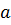 > 0, x > 0), где |x|<<
> 0, x > 0), где |x|<< 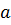 (соотношение А<< B между положительными А и В означает, что А весьма мало по сравнению с В).
(соотношение А<< B между положительными А и В означает, что А весьма мало по сравнению с В).
С помощью этой формулы приближенно вычислить:
174. a) 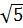 б)
б)  в)
в) 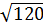
РАСЧЕТНЫЕ ЗАДАНИЯ
Задание № 1
Составить уравнение касательной и нормали кривой в точке М с абсциссой х0
1. 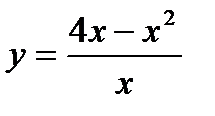 , х0 = 2; 16.
, х0 = 2; 16.  , х0 = 1;
, х0 = 1;
2. у = х – х3, х0 = 1; 17.  , х0 = 1;
, х0 = 1;
3. 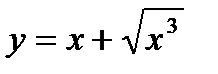 , х0 = 1; 18.
, х0 = 1; 18.  , х0 = 1;
, х0 = 1;
4. 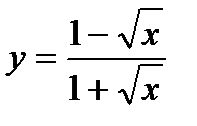 , х0 = 4; 19.
, х0 = 4; 19. 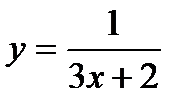 , х0 = 2;
, х0 = 2;
5. у = 2х3 + 3х – 1, х0 = -2; 20. 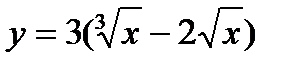 , х0 = 1;
, х0 = 1;
6. 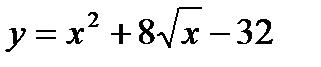 , х0 = 4; 21.
, х0 = 4; 21. 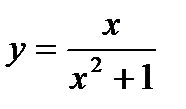 , х0 = -2;
, х0 = -2;
7. 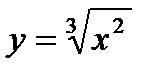 , х0 = -8; 22.
, х0 = -8; 22. 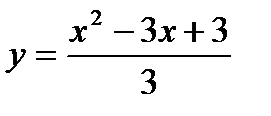 , х0 = 3;
, х0 = 3;
8.  , х0 = 16; 23.
, х0 = 16; 23. 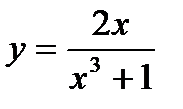 , х0 = 1;
, х0 = 1;
9. у = 2х2 – 3х + 1, х0 = -2; 24. 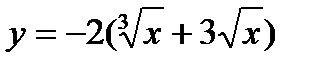 , х0 = 1;
, х0 = 1;
10. 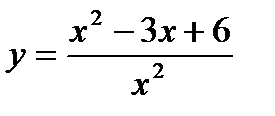 , х0 = 3; 25.
, х0 = 3; 25.  , х0 = 1;
, х0 = 1;
11. 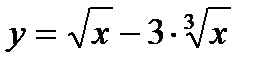 , х0 = 64; 26.
, х0 = 64; 26. 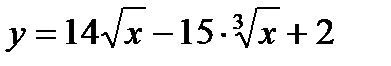 , х0 = 1;
, х0 = 1;
12. 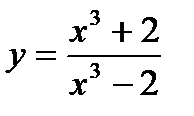 , х0 = 2; 27.
, х0 = 2; 27. 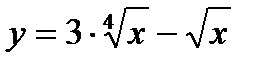 , х0 = 1;
, х0 = 1;
13. у = 2х2 – 3, х0 = 1; 28. 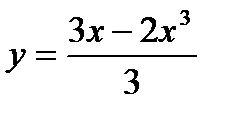 , х0 = 1;
, х0 = 1;
14. 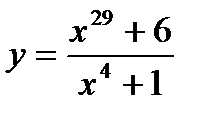 , х0 = 1; 29.
, х0 = 1; 29. 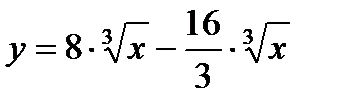 , х0 = 1;
, х0 = 1;
15. 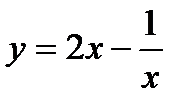 , х0 = 1; 30.
, х0 = 1; 30.  , х0 = 2.
, х0 = 2.
Задание № 2
Найти производную
1. 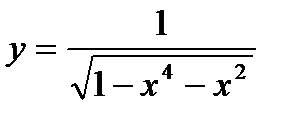 ; ;
| 16.  ; ;
|
2. 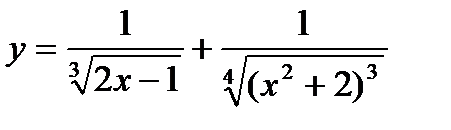 ; ;
| 17.  ; ;
|
3. 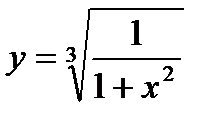 ; ;
| 18. 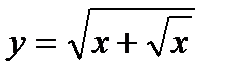 ; ;
|
4. 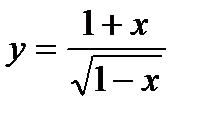 ; ;
| 19. 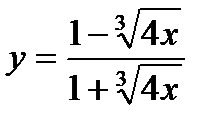 ; ;
|
5.  ; ;
| 20.  ; ;
|
6.  ; ;
| 21. 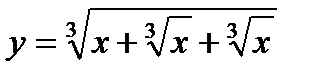 ; ;
|
7. 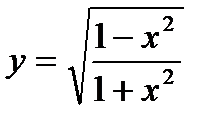 ; ;
| 22. 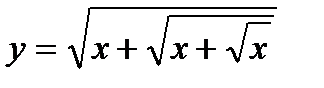 ; ;
|
8. 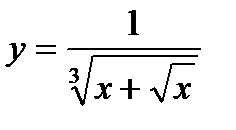 ; ;
| 23. 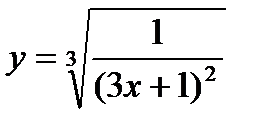 ; ;
|
9.  ; ;
| 24. 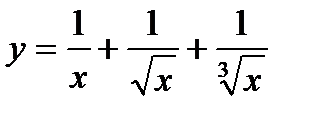 ; ;
|
10. 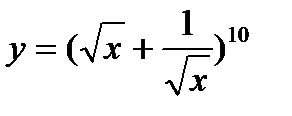 ; ;
| 25. 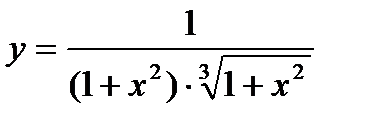 ; ;
|
11.  ; ;
| 26. 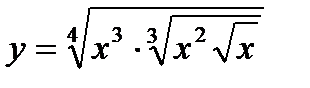 ; ;
|
12. 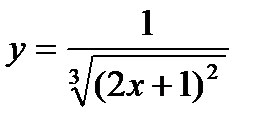 ; ;
| 27. 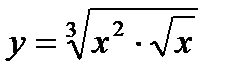 ; ;
|
13. 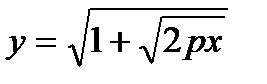 ; ;
| 28. 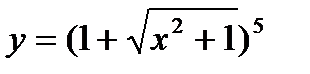 ; ;
|
14. 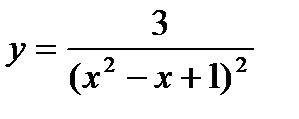 ; ;
| 29. 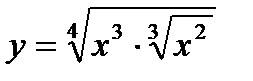 ; ;
|
15. 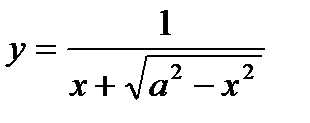 ; ;
| 30. 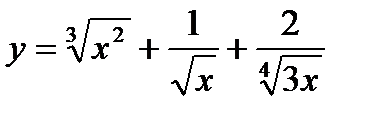 . .
|
Задание № 3
Найти производную
1. 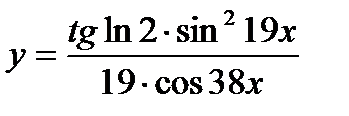 ; ;
| 16.  ; ;
|
2. 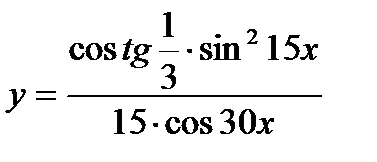 ; ;
| 17.  ; ;
|
3. 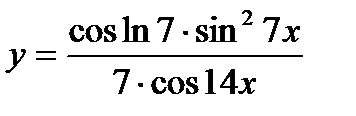 ; ;
| 18. 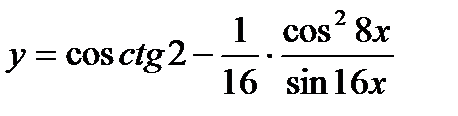 ; ;
|
4. 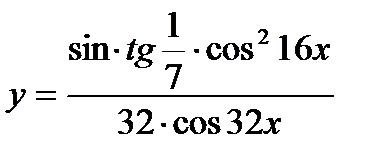 ; ;
| 19. 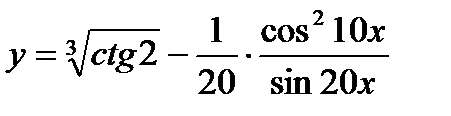 ; ;
|
5. 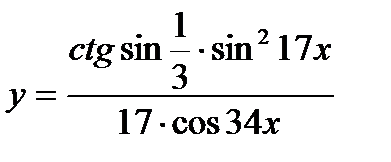 ; ;
| 20. 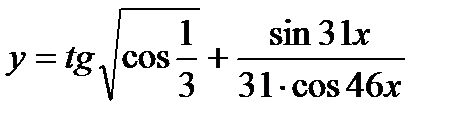 ; ;
|
6. 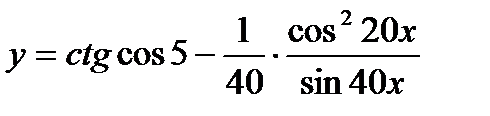 ; ;
| 21. 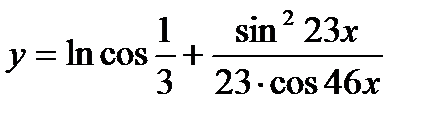 ; ;
|
7. 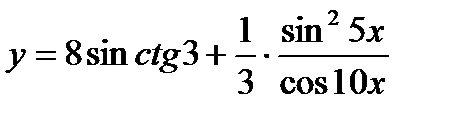 ; ;
| 22. 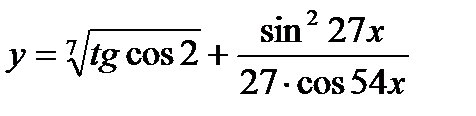 ; ;
|
8.  ; ;
| 23.  ; ;
|
9. 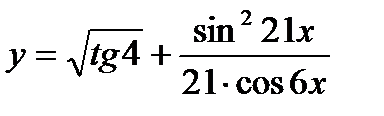 ; ;
| 24. 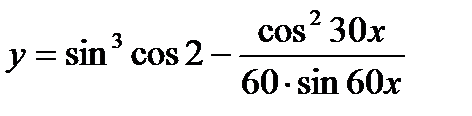 ; ;
|
10. 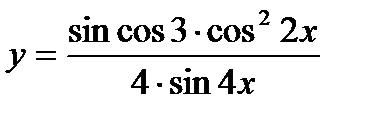 ; ;
| 25.  ; ;
|
11. 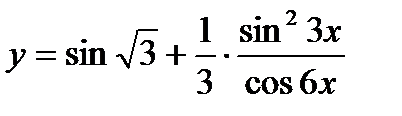 ; ;
| 26.  ; ;
|
12. 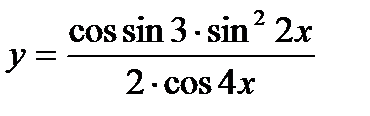 ; ;
| 27. 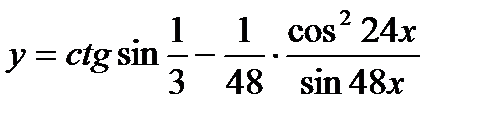 ; ;
|
13. 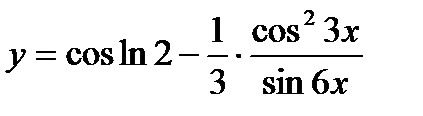 ; ;
| 28. 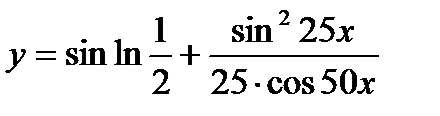 ; ;
|
14. 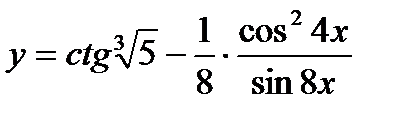 ; ;
| 29. 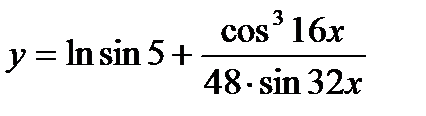 ; ;
|
15.  ; ;
| 30. 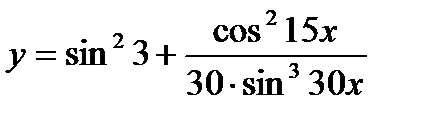 . .
|
Задание №4
Найти производную
1. 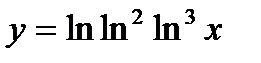 ; ;
| 16. 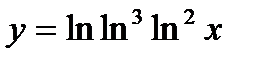 ; ;
|
2. 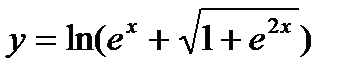 ; ;
| 17. 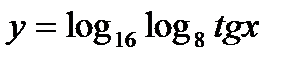 ; ;
|
3. 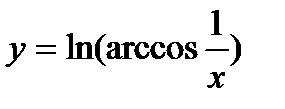 ; ;
| 18.  ; ;
|
4. 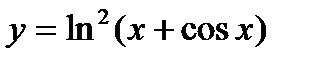 ; ;
| 19. 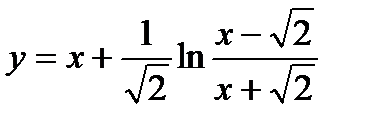 ; ;
|
5. 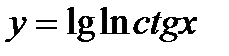 ; ;
| 20. 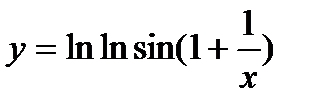 ; ;
|
6. 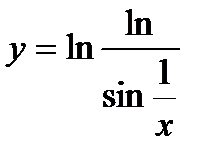 ; ;
| 21. 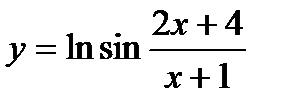 ; ;
|
7. 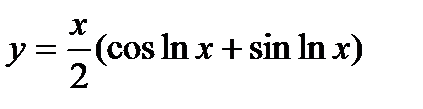 ; ;
| 22. 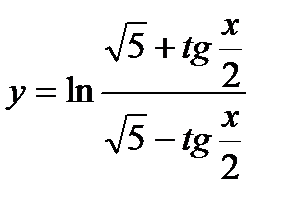 ; ;
|
8. 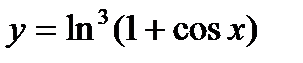 ; ;
| 23. 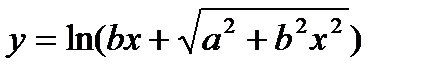 ; ;
|
9. 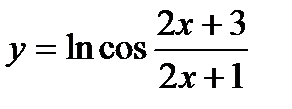 ; ;
| 24. 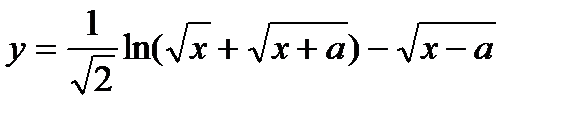 ; ;
|
10. 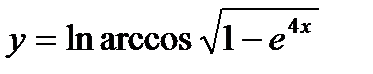 ; ;
| 25. 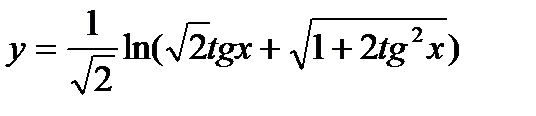 ; ;
|
11.  ; ;
| 26. 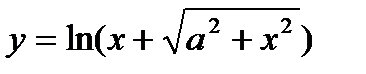 ; ;
|
12.  ; ;
| 27. 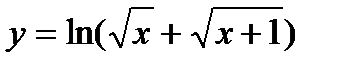 ; ;
|
13. 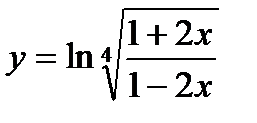 ; ;
| 28.  ; ;
|
14. 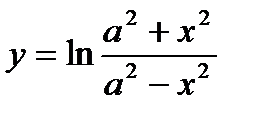 ; ;
| 29. 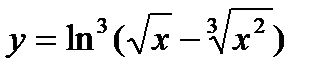 ; ;
|
15. 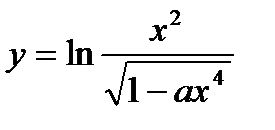 ; ;
| 30. 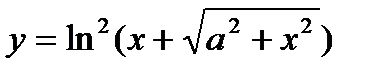 . .
|
Задание №5
Найти производную
1. 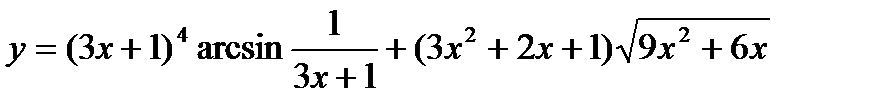 ;
;
2. 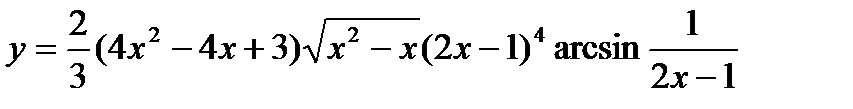 ;
;
3. 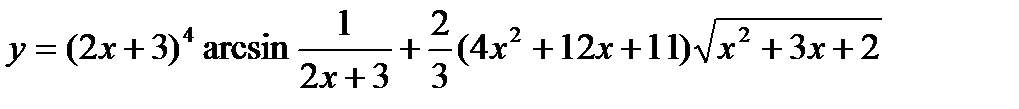 ;
;
4.  ;
;
5. 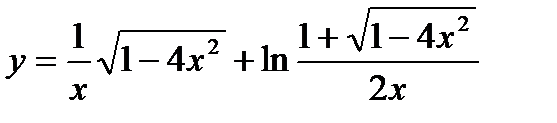 ;
;
6. 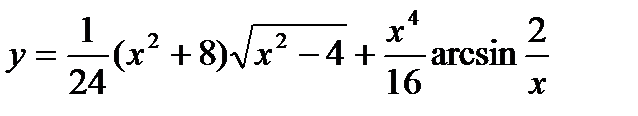 ;
;
7. 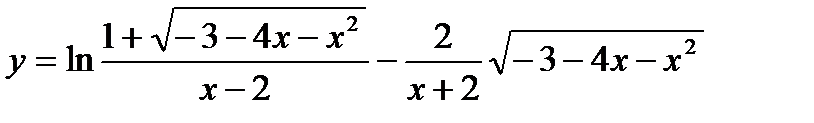 ;
;
8. 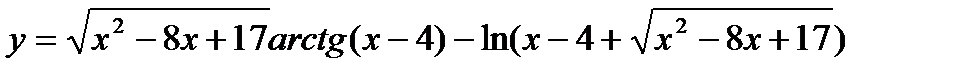 ;
;
9. 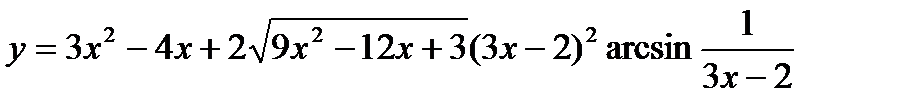 ;
;
10. 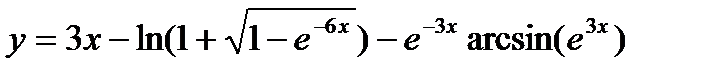 ;
;
11. 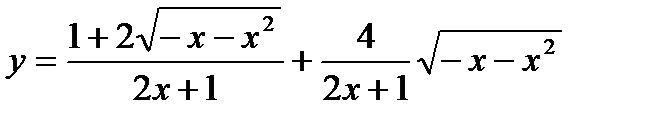 ;
;
12. 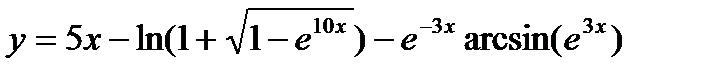 ;
;
13. 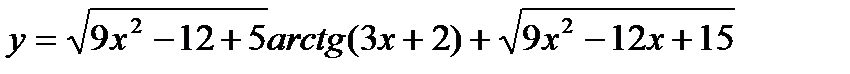 ;
;
14. 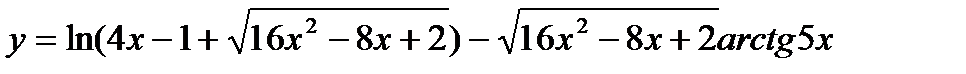 ;
;
15. 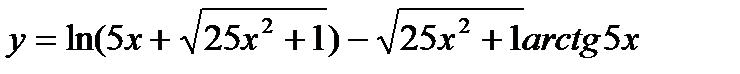 ;
;
16. 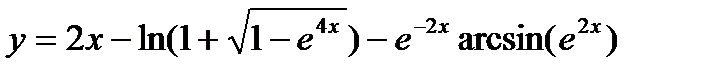 ;
;
17. 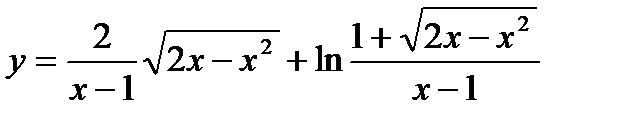 ;
;
18. 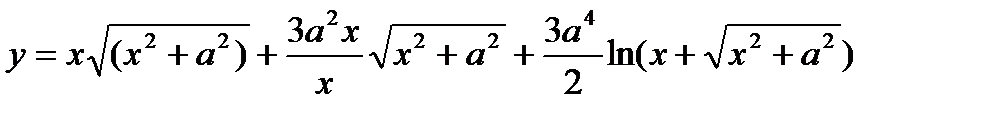 ;
;
19. 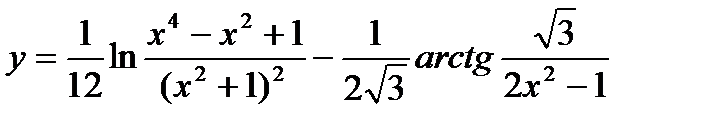 ;
;
20. 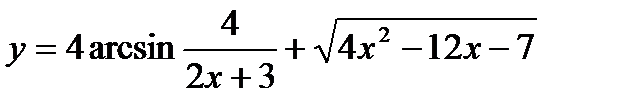 ;
;
21. 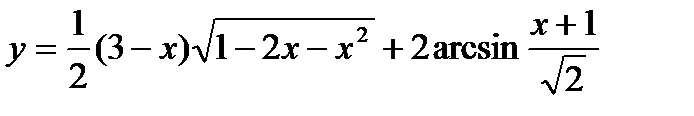 ;
;
22. 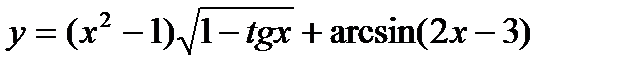 ;
;
23. 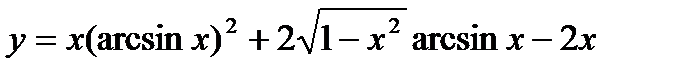 ;
;
24. 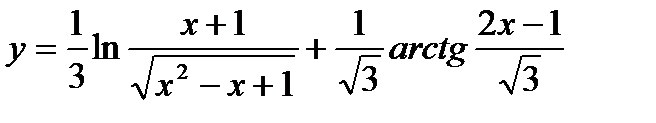 ;
;
25. 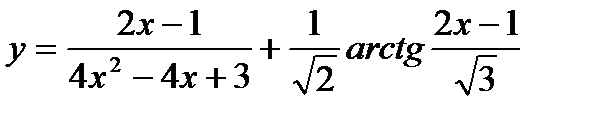 ;
;
26.  ;
;
27. 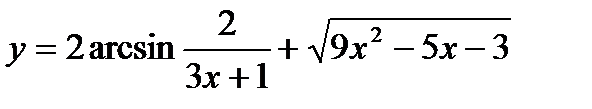 ;
;
28.  ;
;
29. 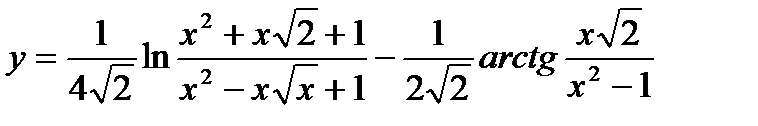 ;
;
30. 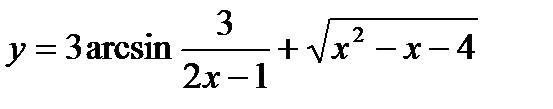 .
.
Задание №6
Найти производную
1. 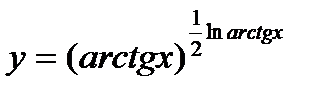 ; ;
| 16. 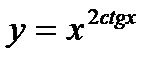 ; ;
|
2. 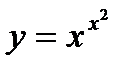 ; ;
| 17. 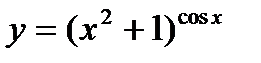 ; ;
|
3. 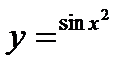 ; ;
| 18.  ; ;
|
4. 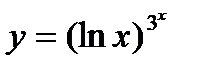 ; ;
| 19.  ; ;
|
5. 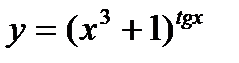 ; ;
| 20.  ; ;
|
6. 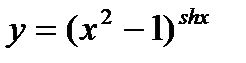 ; ;
| 21. y = (x - 5)ln x; |
| 7. y = x arcsin x; | 22. у = x ctg x; |
8. 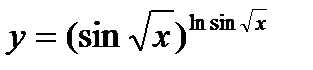 ; ;
| 23. y = x 2 cos x; |
9. 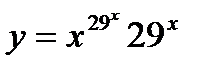 ; ;
| 24.  ; ;
|
10. 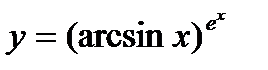 ; ;
| 25. 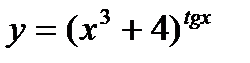 ; ;
|
11. 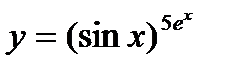 ; ;
| 26. 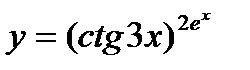 ; ;
|
12. 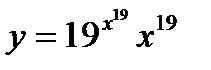 ; ;
| 27. 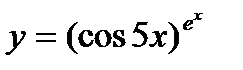 ; ;
|
13. 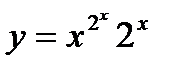 ; ;
| 28. 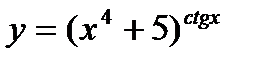 ; ;
|
14. 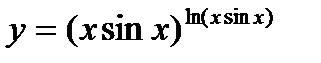 ; ;
| 29. 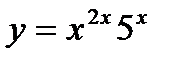 ; ;
|
15. 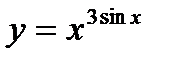 ; ;
| 30. 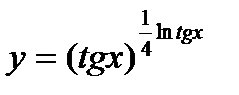 . .
|
Задание №7
Найти производную указанного порядка
1. 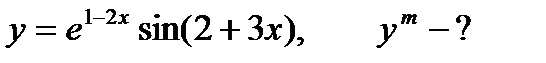 ; ;
| 16. 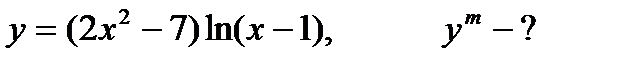 ; ;
|
2. 
| 17. 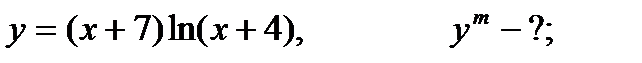
|
3. 
| 18. 
|
4. 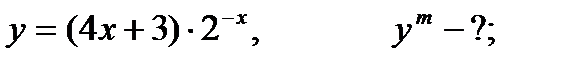
| 19. 
|
5. 
| 20. 
|
6. 
| 21. 
|
7. 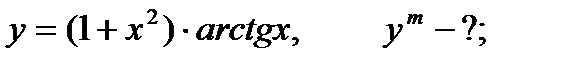
| 22. 
|
8. 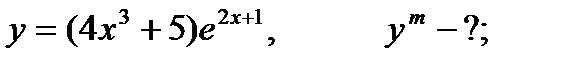
| 23. 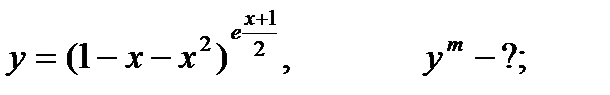
|
9. 
| 24. 
|
10. 
| 25. 
|
11. 
| 26. 
|
12. 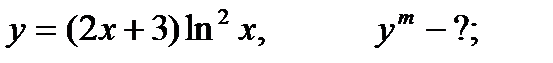
| 27. 
|
13. 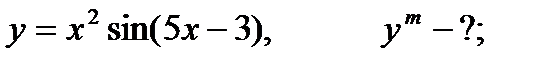
| 28. 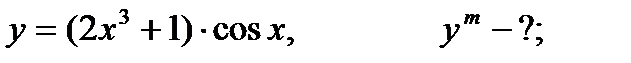
|
14. 
| 29. 
|
15. 
| 30. 
|
Задание №8
Составить уравнение касательной и нормали к кривой в точке, соответствующей значению параметра t0
1. 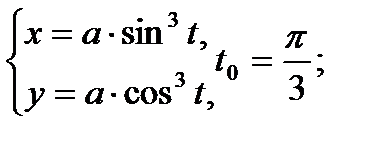
| 16. 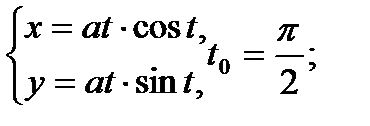
|
2. 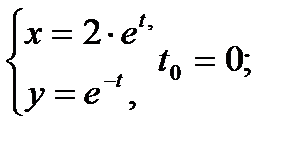
| 17. 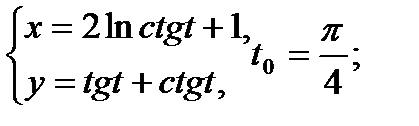
|
3. 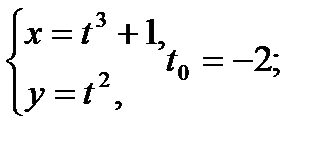
| 18. 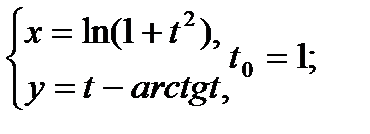
|
4. 
| 19. 
|
5. 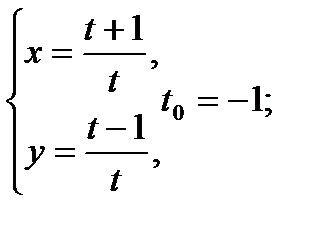
| 20. 
|
6. 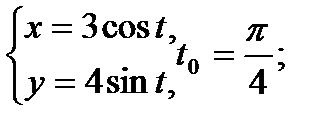
| 21. 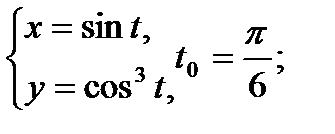
|
7. 
| 22. 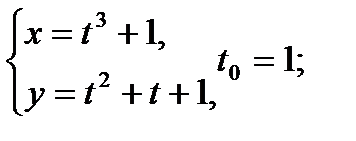
|
8. 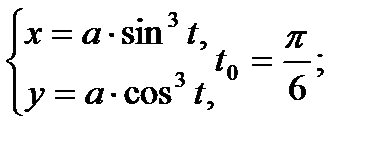
| 23. 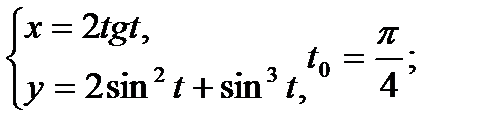
|
9. 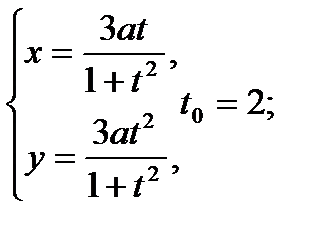
| 24. 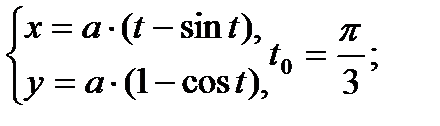
|
10. 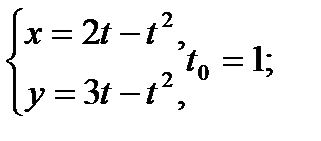
| 25. 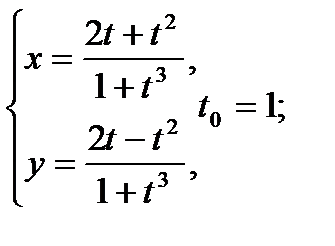
|
11. 
| 26. 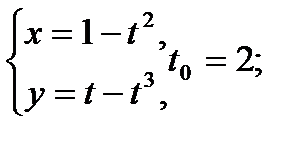
|
12. 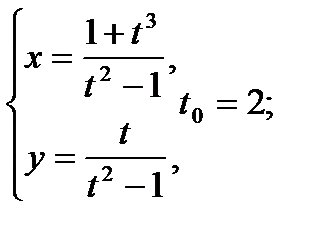
| 27. 
|
13. 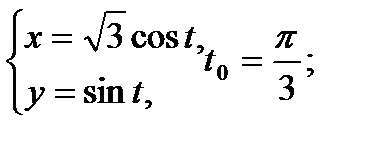
| 28. 
|
14. 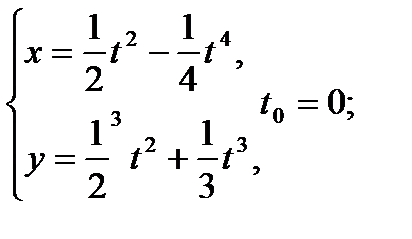
| 29. 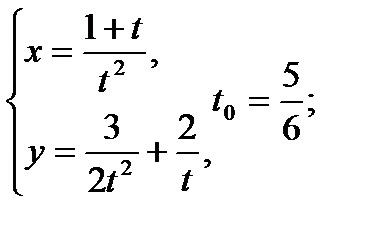
|
15. 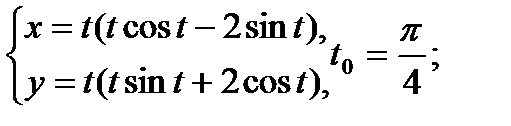
| 30. 
|
Задание №9
Найти производную функции, заданной неявно
1. 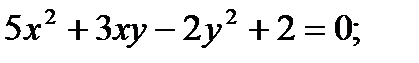
| 16. 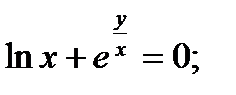
|
2. 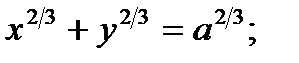
| 17. 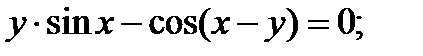
|
3. 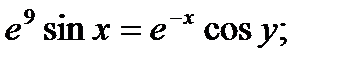
| 18. 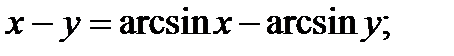
|
4. 
| 19. 
|
5. 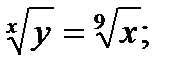
| 20. 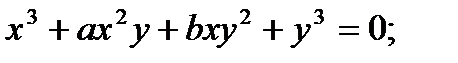
|
6. 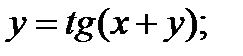
| 21. 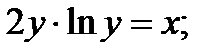
|
7. 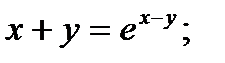
| 22. 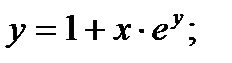
|
8. 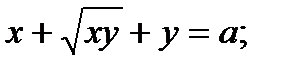
| 23. 
|
9. 
| 24. 
|
10. 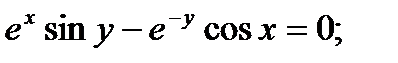
| 25. 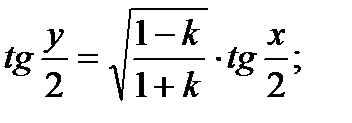
|
11. 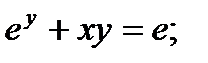
| 26. 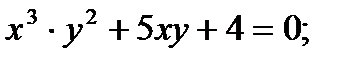
|
12. 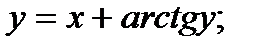
| 27. 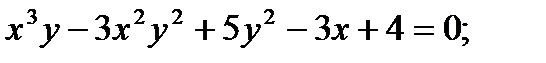
|
13. 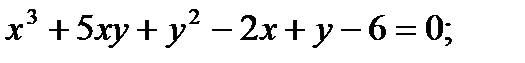
| 28. 
|
14. 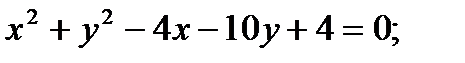
| 29. 
|
15. 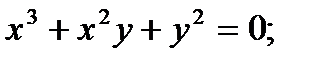
| 30. 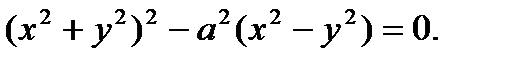
|
Задание №10
Найти дифференциал dy и показать, что функция у удовлетворяет уравнению (1)
1. 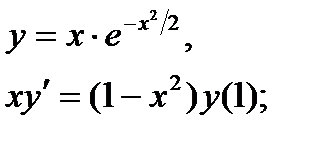
| 16. 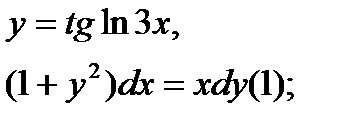
|
2. 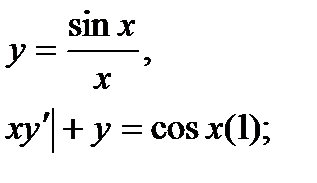
| 17. 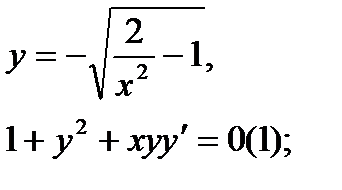
|
3. 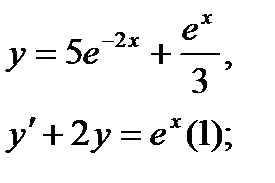
| 18. 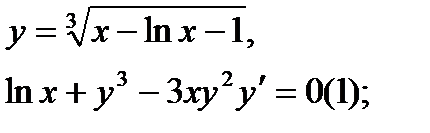
|
4. 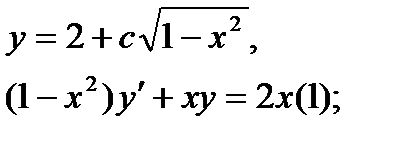
| 19. 
|
5. 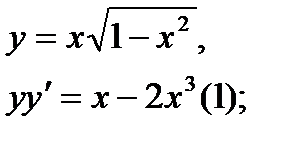
| 20. 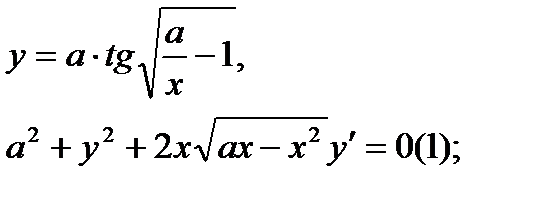
|
6. 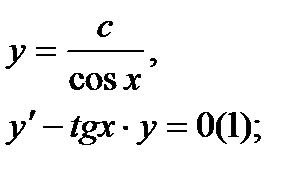
| 21. 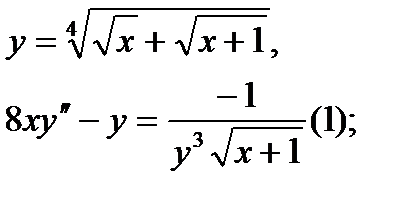
|
7. 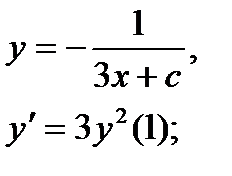
| 22. 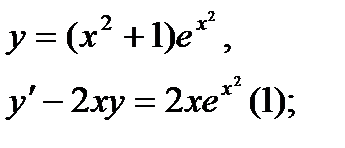
|
8. 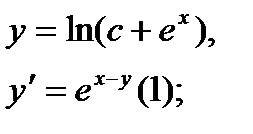
| 23. 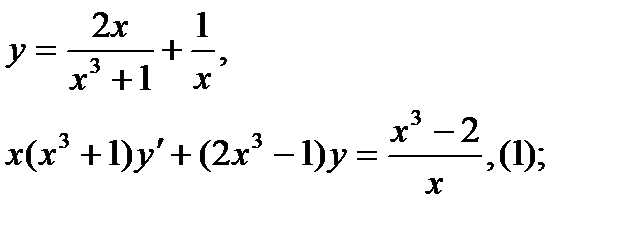
|
9. 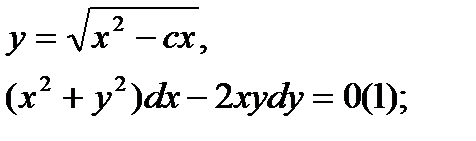
| 24. 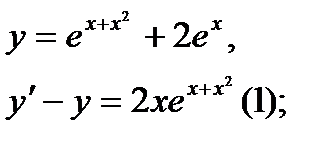
|
10. 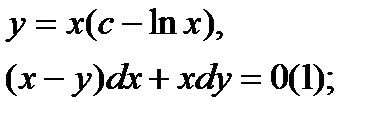
| 25. 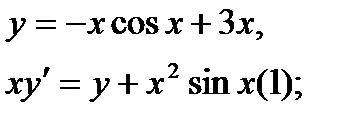
|
11. 
| 26. 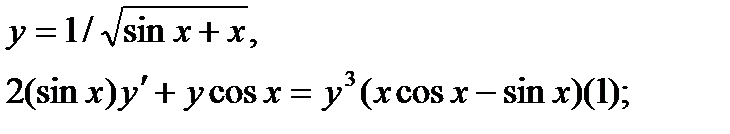
|
12. 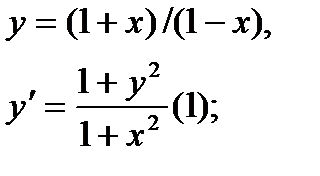
| 27. 
|
13. 
| 28. 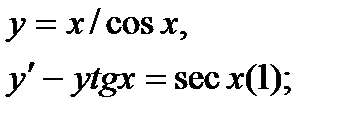
|
14. 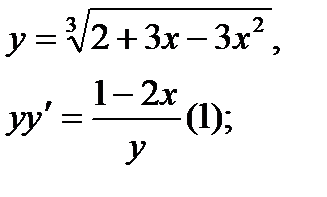
| 29. 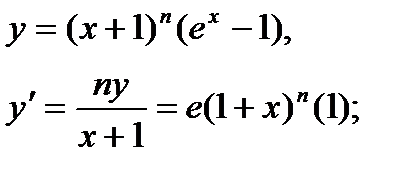
|
15. 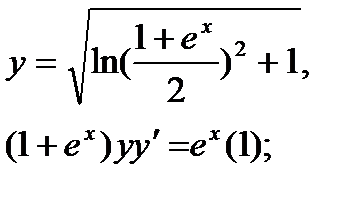
| 30. 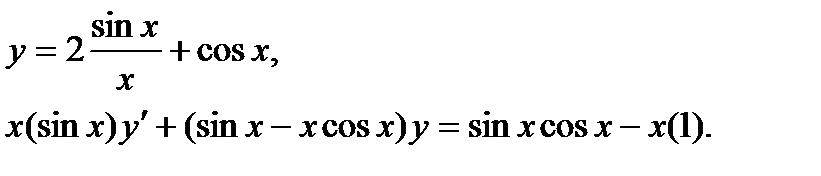
|
Задание №11
Вычислить приближенно
1. 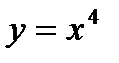
| при х = 3,998; |
2. 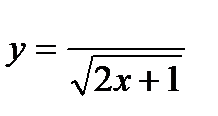
| при х = 1,56; |
3. 
| при х = 7,76; |
4. 
| при х = 0,08; |
5. 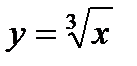
| при х = 26,46; |
6. 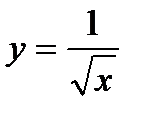
| при х = 4,16; |
7. 
| при х = 1,97; |
8. 
| при х = 1,012; |
9. 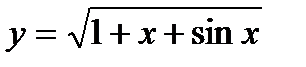
| при х = 0,01; |
10. 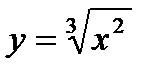
| при х = 1,03; |
11. 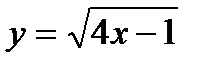
| при х = 2,56; |
12. 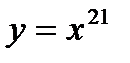
| при х = 0,998; |
13. 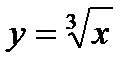
| при х = 8,24; |
14. 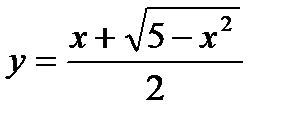
| при х = 0,98; |
15. 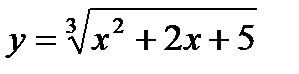
| при х = 0,97; |
16. 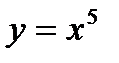
| при х = 2,997; |
17. 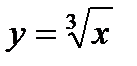
| при х = 1,21; |
18. 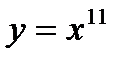
| при х = 1,021; |
19. 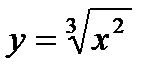
| при х = 1,03; |
20. 
| при х = 27,54; |
21. 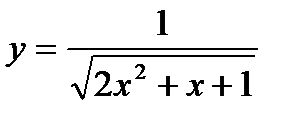
| при х = 1,018; |
22. 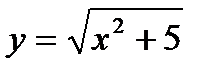
| при х = 1,97; |
23. 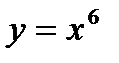
| при х = 2,01; |
24. 
| при х = 7,64; |
25. 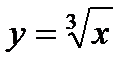
| при х = 8,34; |
26. 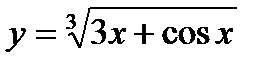
| при х = 0,01; |
27. 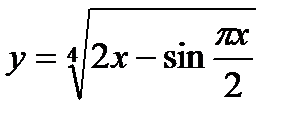
| при х = 1,02; |
28. 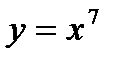
| при х = 2,002; |
29. 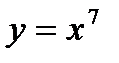
| при х = 1,998; |
30. 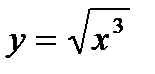
| при х = 0,98. |
Задание №12
Вычислить пределы функций, применяя правило Лопиталя
1. 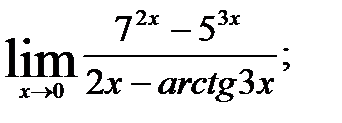
| 16. 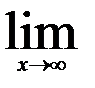 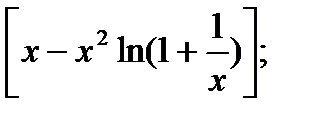
|
2. 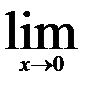 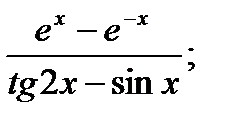
| 17.  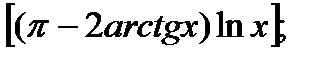
|
3. 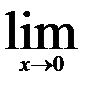 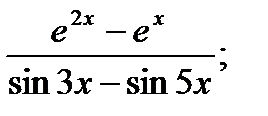
| 18. 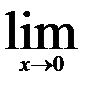 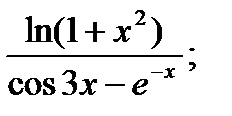
|
4. 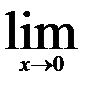 
| 19. 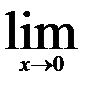 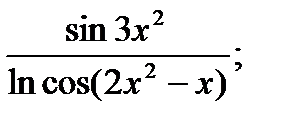
|
5. 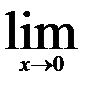 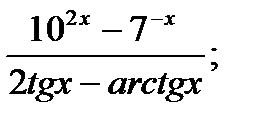
| 20. 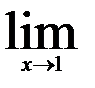 
|
6. 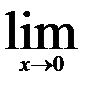 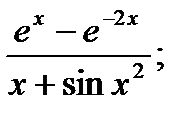
| 21. 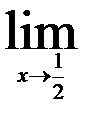 
|
7.  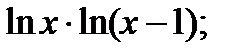
| 22. 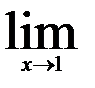 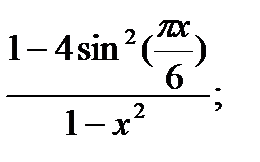
|
8.  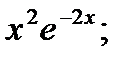
| 23. 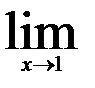 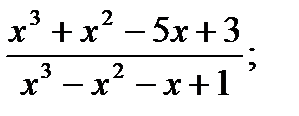
|
9. 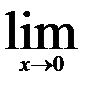 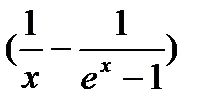 ; ;
| 24. 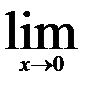 
|
10. 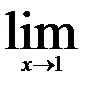 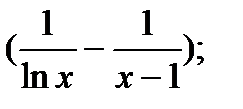
| 25. 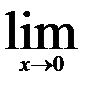 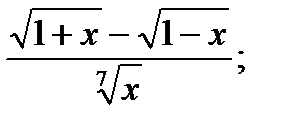
|
11. 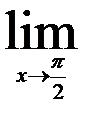 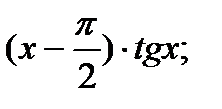
| 26. 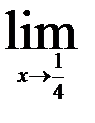 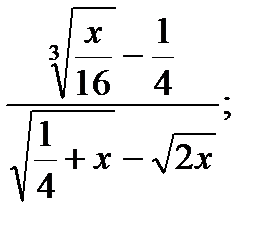
|
12.  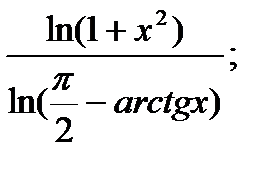
| 27. 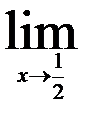 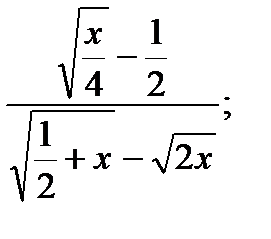
|
13. 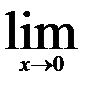 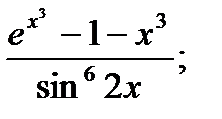
| 28. 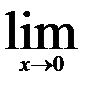 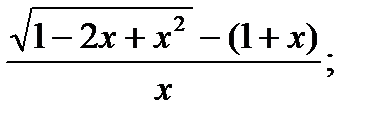
|
14.  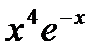 ; ;
| 29. 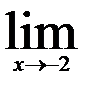 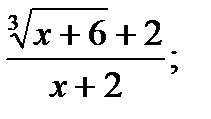
|
15. 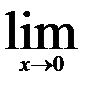 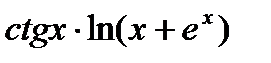 ; ;
| 30. 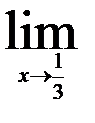 
|
Задание № 13
Вычислить пределы функций, применяя правило Лопиталя
1. 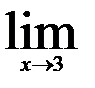 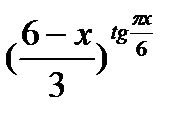 ; ;
| 16. 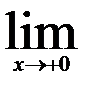 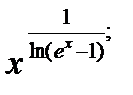
|
2. 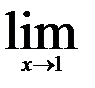 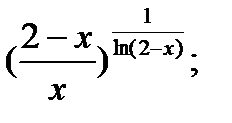
| 17. 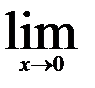 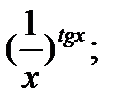
|
3. 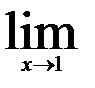 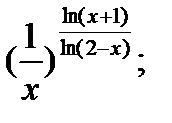
| 18. 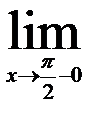 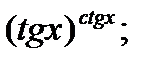
|
4. 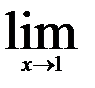 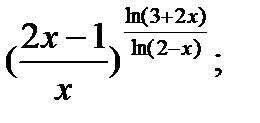
| 19. 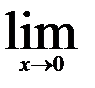 
|
5. 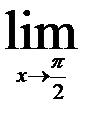 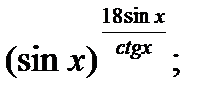
| 20. 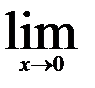 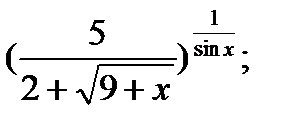
|
6. 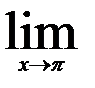 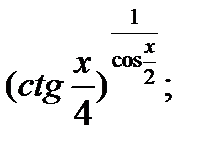
| 21. 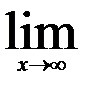 
|
7. 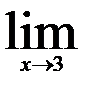 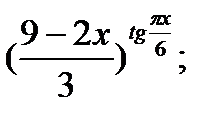
| 22. 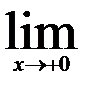 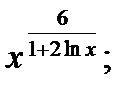
|
8.  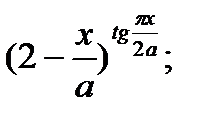
| 23. 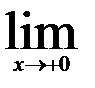 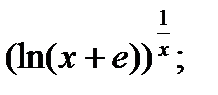
|
9. 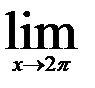 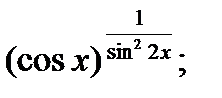
| 24. 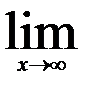 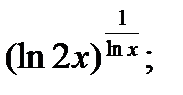
|
10.  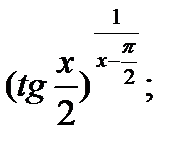
| 25. 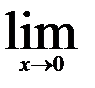 
|
11. 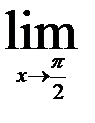 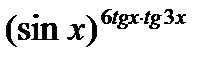 ; ;
| 26. 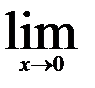 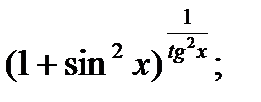
|
12. 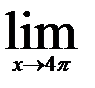 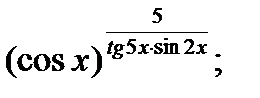
| 27. 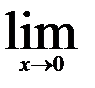 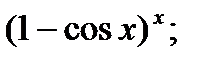
|
13. 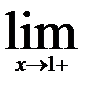 
| 28. 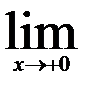 
|
14. 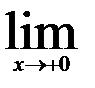 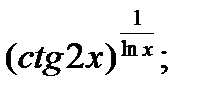
| 29. 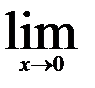 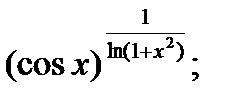
|
15. 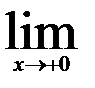 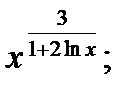
| 30.  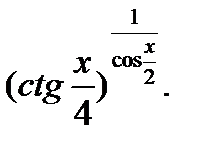
|
Задание № 14
Исследовать на экстремум следующие функции
1. 
| 16. 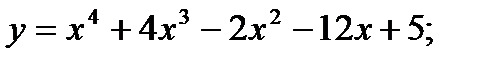
| |||||
2. 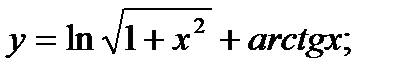
| 17. 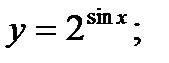
| |||||
3. 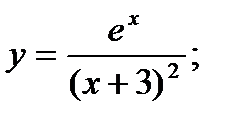
| 18. 
| |||||
4. 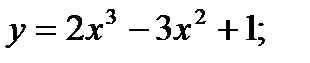
| 19. 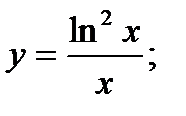
| |||||
5. 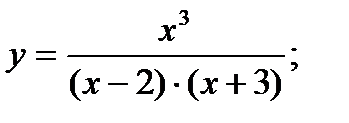
| 20. 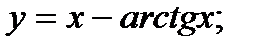
| |||||
6. 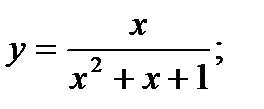
| 21. 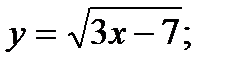
| |||||
7. 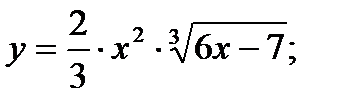
| 22. 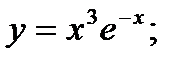
| |||||
8. 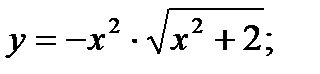
| 23. 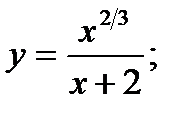
| |||||
9. 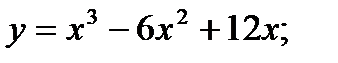
| 24. 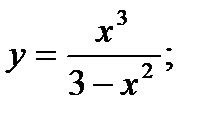
| |||||
10. 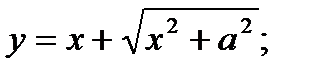
| 25. 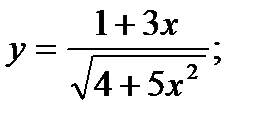
| |||||
11. 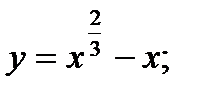
| 26. 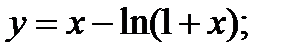
| |||||
12. 
| 27. 
| |||||
13. 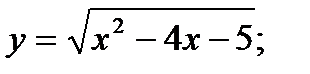
| 28. 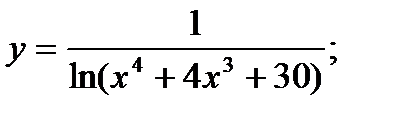
| |||||
14. 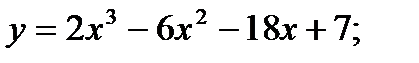
| 29. 
| |||||
15. 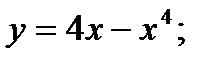
| 30. 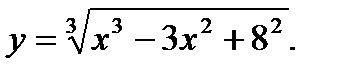
Дата добавления: 2016-11-18; Мы поможем в написании ваших работ!; просмотров: 1204 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.161 с.






