Уфа 2010
УДК 51
ББК 22.14
М 54
Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства (протокол № 2 от 24 февраля 2010 года)
Составители: доцент Костенко Н.А., доцент Авзалова З.Т.
Рецензент: доцент кафедры бухгалтерского учета и аудита Насырова А.Д.
Ответственный за выпуск: зав каф. математики доцент Лукманов Р.Л.
Производная функции
Производной функции у= f(х) по аргументу х называется предел к которому стремится отношение приращения функции Δу к приращению аргумента Δх, когда приращение аргумента Δх стремится к нулю.
Для обозначения производной функции у= f(х) употребляются следую-щие символы: y′ или f′(x) – обозначения Лангранжа,  - обозначения Лейбница.
- обозначения Лейбница.
Таким образом, по самому определению имеем
 (1)
(1)
Если предел (1) существует в каждой точке некоторого промежутка, то производная является функцией от x на этом промежутке. Для данного же фиксированного значения аргумента х производная есть определенное число. Для обозначения производной в данной точке х=а употребляют запись y′(a) или f′(a). Операция отыскивания производной f′(x) называется дифферен-цированием функции.
Если функция s=f(t) выражает собой закон движения материальной точки, где s – путь, пройденной точкой, а t – время, то v=s′=f′(x) есть скорость движения. В этом состоит механический смысл производной.
Если кривая задана уравнением y=f′(x), то значение производной при данном фиксированном значении аргумента x0, то есть в точке М0(x0,y0), равно тангенсу угла наклона касательной, произведенной к кривой в точке М0(x0,y0).
Таким образом
y′(x0)=tgφ=kkac
где φ- угол наклона касательной, а k – ее угловой коэффициент.
Основные формулы дифференцирования
Нахождение производной по определению (этот способ называется непосредственным дифференцированием) является громоздким и затруднительным. На практике им пользуются при выводе основных формул и правил дифференцирования элементарных функций.
Во всех последующих формулах С – постоянная величина, а u и v некоторые функции от аргумента x, имеющие производные u′ и v′.
Сформулируем основные правила дифференцирования:
1. (C)′=0 (C - const)
2. (x)′=1
3. y=u±v, то y′=u′±v′
4. y=  , то y′=
, то y′= 
5. y=uv, то y′=u′v+uv′
6. Производной сложной функции y=f(u), где u=(x) по аргументу х равна произведению производной данной функции у по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х, т.е. если соответствующих друг другу значений x и u существуют производные.
 и
и  , то
, то  или y′x=yu′∙ ux′
или y′x=yu′∙ ux′
Производные основных элементарных функций находятся по следующим формулам, каждая из которых может быть выведена исходя из определения производной и указанных выше теорем.
Таблица производных
( )′=α∙uα-1∙u′ (1)
)′=α∙uα-1∙u′ (1)
( ) ′= -
) ′= - 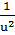 ∙u′ (1а)
∙u′ (1а)
( ) ′=
) ′=  ∙u′ (1б)
∙u′ (1б)
( ) ′=
) ′=  ∙lna∙u′ (2)
∙lna∙u′ (2)
( ) ′=
) ′=  ∙u′ (2a)
∙u′ (2a)
(ln u)′=  ∙u′ (3)
∙u′ (3)
( )=
)=  ∙u′ (3a)
∙u′ (3a)
(sin u)′=cos u∙u′ (4)
(cos u)′=-sin u∙u′ (5)
(tg u)′ = 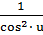 ∙u′ (6)
∙u′ (6)
(ctg u)′= -  ∙u′ (7)
∙u′ (7)
(arcsin u)′=  ∙u′ (8)
∙u′ (8)
(arccos u)′= -  ∙u′ (9)
∙u′ (9)
(arctg u)′=  ∙u′ (10)
∙u′ (10)
(arcctg u)′= -  ∙u′ (11)
∙u′ (11)






