Лабораторная работа № 2.1
Определение коэффициента Пуассона методом адиабатного расширения и
сжатия
(учебно-методическое пособие)
Составил доц. Харин Г.Г.,
Утверждено на заседании кафедры
29 сентября 2011 г., протокол № 2
Одесса - 2011
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Все термодинамические процессы совершаются в соответствии с законом сохранения и превращения энергии (первый закон термодинамики):
Теплота dQ, сообщаемая термодинамической системе в процессе теплообмена,идёт на совершение работы dA против внешних сил и на изменение внутренней энергии системы dU
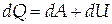
| (1.1) |
Теплота dQ есть мера переданной системе энергии хаотического движения молекул, которая приводит к изменению температуры системы dT:

| (1.2) |
где M - масса системы, µ -масса одного моля вещества, CP - молярная теплоёмкость вещества при изобарном процессе (P=const).
Молярная теплоёмкость численно равна количеству теплоты,необходимому для нагревания одного моля вещества на один Кельвин.

|
Элементарная работа, совершаемая газом против внешних сил, равна

| (1.3) |
где Р - внешнее давление, а dV - изменение объёма газа.
Внутренняя энергия термодинамической системы равна сумме кинетической энергии хаотического движения молекул (атомов) и потенциальной энергии взаимодействия между ними и является функцией состояния термодинамической системы U=U(T,V). В идеальном газе взаимодействием молекул можно пренебречь, поэтому внутренняя энергия идеального газа зависит лишь от температуры U=U(T):
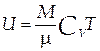
| (1.4) |
где CV - молярная теплоёмкость при изохорном процессе (V=const).
Изменение внутренней энергии идеального газа пропорционально изменению его температуры:

| (1.5) |
Распределение тепла, сообщаемого системе на выполнение работы и изменение внутренней энергии, зависит от вида процесса.
При изотермическом процессе (T=const, dT=0, dU=0), следовательно всё тепло, сообщённое системе, идёт на совершение работы:

| (1.6) |
При изохорном процессе (V=const, dV=0, dA=0), следовательно всё тепло, сообщённое системе, идёт на изменение внутренней энергии системы:

| (1.7) |
При изобарном процессе (P=const)

| (1.8) |
1.2. ТЕПЛОЁМКОСТЬ ГАЗА ПРИ РАЗЛИЧНЫХ ИЗОПРОЦЕССАХ
Теплоёмкость газа зависит от того, какой процесс совершается над газом.
При изотермическом процессе (T=const, dT=0)

|
При изохорном процессе теплота идёт только на изменение внутренней энергии газа, поэтому

|
При изобарном процессе

|
Здесь мы воспользуемся уравнением Менделеева-Клапейрона PV=RT, из которого (при P=const) следует PdV/dT=R. Примая во внимание приведенное выше выражение для изохорной теплоемкости, получим формулу Майера:

| (1.9) |
Молярная теплоемкость идеального газа при постоянном давлении больше его теплоемкости при постоянном объеме на величину универсальной газовой постоянной. Это связано с тем, что в изохорном процессе тепло идёт только на нагрев газа (увеличение его внутренней энергии), а при изобарном процессе тепло, подводимое к газу, расходуется не только на его нагрев, но и на совершение работы против внешних сил.
1. 3. АДИАБАТНЫЙ ПРОЦЕСС
Адиабатным называется такой процесс, который протекает без теплообмена с окружающей средой (dQ= 0 ).
Теплоёмкость газа, совершающего адиабатный процесс, равна нулю.
Первый закон термодинамики для адиабатного процесса записывается в виде:

| (1.10) |
Тогда
 или или 
|
Отсюда видно, что если газ адиабатно расширяется (dV>0), то он совершает положительную работу (dA>0) и, следовательно, dU<0, т.е. газ совершает работу за счёт убыли внутренней энергии системы, что приводит к её охлаждению (dT<0).
Если же газ адиабатно сжимается то dA<0, dU>0 и dT>0,т.е. газ нагревается. На этом основано явление так называемого пневматического огнива, которое находит применение в дизелях, где зажигание горючей смеси осуществляется путем адиабатного сжатия.
При адиабатном процессе изменяются все параметры газа P, V и T. Взаимосвязь между этими параметрами даётся уравнением Пуассона, вывод которого приведём для одного моля идеального газа.
Подставляя в уравнение (1.10) выражения для dA и dU из (1.3) и (1.5), получим:

| (1.11) |
Выразим из уравнения Менделеева-Клапейрона давление P и подставим в (1.11):

|
Из формулы Майера найдём R и разделим на CV:

| (1.12) |
где g = Ср./CV - коэффициент Пуассона.
Проинтегрировав (1.12), получим уравнение Пуассона:

| (1.13) |
Выразив Т из уравнения Менделеева-Клапейрона и подставив в (1.13), получим вторую запись уравнения Пуассона:

| (1.14) | ||
      Зависимость P =f(V) в адиабатном процессе описывается кривой, называемой адиабатой. В координатах (P,V) адиабата идёт круче изотермы (PV=const), так как показатель адиабаты больше единицы (g >1) (рис.1) Зависимость P =f(V) в адиабатном процессе описывается кривой, называемой адиабатой. В координатах (P,V) адиабата идёт круче изотермы (PV=const), так как показатель адиабаты больше единицы (g >1) (рис.1)
| P Изотерма Адиабата V Рис.1 | ||
Можно также показать, что показатель адиабаты связан с числом степеней свободы* молекул і следующим соотношением  . Из этого следует также, что показатель адиабаты имеет также верхнюю числовую границу (
. Из этого следует также, что показатель адиабаты имеет также верхнюю числовую границу ( ). Тогда
). Тогда 
*)Число степеней свободы – это число независимых координат при помощи которых можно определить положение тела (молекулы).
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
2.1. ЦЕЛЬ РАБОТЫ: Определение коэффициента Пуассона для воздуха.
2.2. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: сосуд, манометр, резиновая груша.
2.3. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА.
Схема экспериментальной установки показана на рис.2. Сосуд 1 сообщается с окружающим воздухом через патрубок 3. Клапаном 4 регулируют поступление воздуха в сосуд. Давление воздуха в сосуде, избыточное над атмосферным, измеряют жидкостным манометром.

| |
| Рис.2 | Рис.3 |
Так как уровень манометрической жидкости может не совпадать с нулём шкалы манометра, то при определении давления в сосуде необходимо отсчитывать смещение обоих менисков жидкости
относительно нуля шкалы. Сумма этих двух отсчётов a+b=h (рис.3) даст высоту столба манометрической жидкости, гидростатическое давление которого равно избытку давления в сосуде по сравнению с внешним атмосферным давлением Pa. Таким образом, абсолютное давление газа в сосуде равно сумме атмосферного давления и давления столба жидкости высотой h в манометре.
2.4. ПОРЯДОК ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ




