Формулировки
1) Матрица, операции над матрицами, их свойства
2) Система линейных уравнений, матричная запись
3) Модель Леонтьева «затраты-выпуск», сведение задачи к системе линейных уравнений
4) Обратная матрица
5) Перестановки, инверсия, четность перестановки, транспозиции.
6) Определитель n-го порядка
7) Свойства определителя
8) Элементарные преобразования над строками и столбцами матрицы
9) Минор элемента и алгебраическое дополнение
10) Формула разложения определителя по строке или столбцу
11) Взаимная матрица. Теорема о существовании обратной матрицы (формулировка)
12) Формулы Крамера
13) Линейное пространство, примеры. Подпространство линейного пространства
14) Линейно зависимые и линейно независимые системы векторов
15) Линейная оболочка системы векторов. Теорема о линейной зависимости
16) Базис линейного пространства. Теорема о размерности линейного пространства
17) Формулировка теоремы о преобразовании координат вектора при смене базиса
18) Минор k-ого порядка матрицы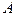 
, определение ранга матрицы
19) Теорема о сохранении ранга матрицы при элементарных преобразованиях
20) Формулировка теоремы о ранге матрицы
21) Формулировка теоремы о ранге произведения матриц
22) Формулировка теоремы Кронекера-Капелли
23) Элементарные преобразования системы линейных уравнений
24) Однородная и неоднородная система линейных уравнений.
25) Определение базисных строк и столбцов матрицы.
26) Определение базисных и свободных переменных, фундаментальной совокупности решений, частного и общего решения неоднородной системы.
27) Формулировка теоремы о числе решений
28) Альтернативы Фредгольма
29) Собственное число и собственный столбец (вектор) матрицы
30) Характеристический многочлен матрицы
31) Свойства собственных векторов матрицы
Прошу особое внимание обратить на ПРИМЕРЫ к определениям (примеры линейных пространств, примеры линейно зависимых и линейно независимых систем, примеры базисов). В задании обязательно будет предложено привести примеры.
Доказательства
1) Доказать, что (А + В)С = АС + ВС и А(ВС) = (АВ)С
2) Доказать, что (АВ)Т= ВТАТ
3) Доказательство теоремы о смене четности перестановки при транспозиции
4) Доказательство одного из свойств определителя (из доказанных на лекции)
5) Доказательство формулы разложения определителя по строке или столбцу
6) Теорема о взаимной матрице
7) Теорема о существовании обратной матрицы
8) Доказательство единственности обратной матрицы
9) Доказательство формул Крамера
10) Доказательство утверждения 3 теоремы о линейной зависимости
11) Доказательство утверждения 4 теоремы о линейной зависимости
12) Доказательство формулы преобразовании координат вектора при смене базиса.
13) Теорема о приведении матрицы к ступенчатому виду
14) Теорема о ранге матрицы
15) Теорема Кронекера-Капелли
16) Однородная система n уравнений с n неизвестными имеет ненулевое решение тогда и только тогда, когда определитель этой системы равен нулю
17) Теорема о связи собственных чисел и корней характеристического многочлена
Практические задания
1) Нахождение обратной матрицы (при n = 3)
2) Нахождение коммутирующей матрицы (при n = 2)
3) Пример на нахождение ранга матрицы
4) Проверка линейной независимости системы векторов
5) Выделения базиса в линейной оболочке
6) Нахождение координат вектора относительно данного базиса
7) Нахождение матрицы перехода от одного данного базиса к другому
8) Решение системы линейных уравнений методом Гаусса
9) Пример на построение фундаментальной совокупности решений
10) Пример на нахождение собственных чисел и собственных векторов матрицы
Пример задания коллоквиума
1. (1 балл) Дать определение линейно зависимой и линейно независимой системы векторов.
2. (1 балл) Привести два примера линейного пространства и базиса в нем.
3. (3 балла) Сформулировать и доказать формулу преобразования координат вектора при смене базиса.
4. (1 балл) Дана система векторов а1, а2, а3, а4. Докажите, что линейные оболочки векторов а1, а2, а3, а4 и а1, а1+а2, а2-а3, а3+a4 совпадают.
5. (1 балл) Найти собственные числа и собственные векторы матрицы 
6. (3 балла) Пусть Е = (е1, е2, е3, е4) базис в R4. Заданы векторы а1 = 2е1– 3е2+е3–2е4, а2 = 3е1+е2–2е3+е4, а3 = –4е1–5е2+5е3–4e4, а4 = е1+4е2–3е3+3е4.
а) Найдите размерность и базис линейной оболочки Lin(a1, a2, a3, a4).
б)Найдите разложение вектора x= 3е1+е2–2е3+е4 в выбранном базисе.
