ЛАБОРАТОРНАЯ РАБОТА № 4
1. Радиус R и высота H конуса могут изменяться в пределах: от 0,1 до 0,2
с шагом 0,05 и от 1,5 до 2,5 с шагом 0,5 соответственно
Получить таблицу изменения объема V и его полной поверхности S.
2. Определить n-троек натуральных чисел, удовлетворяющих уравнению
X 2 + Y 2 + Z 2 = 3 X Y Z.
Получить результат при n= 5.
3. Шестизначное число называется “ счастливым “, если у него сумма первых трех цифр равна сумме последних трех.
Найти количество “счастливых “ шестизначных чисел, у которых сумма трех цифр равна n. Получить результат при n = 5.
4. Получить таблицу значений функции при изменении переменной “ x“ от 0 до 1 с шагом 0,5 и переменной “ y “ от 2 до 4 с шагом 0,1.
U = 
5. Определить трехзначное число, обладающее следующим свойством: число начинается цифрой 4. Если эту цифру перенести в конец числа, получим число, составляющее 3/4 исходного числа. Вывести на печать оба числа.
6. Вычислить сумму вида: 
Получить результат при n= 7, k= 6.
7. Получить таблицу значений функции при изменении “х” от 0,2 до 1,2 с шагом 0,4 и при изменении “y” от 0,5 до 2,5 с шагом 1.
U= max { ln z2; y2 + сos x}, где Z =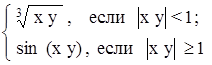 
8. Получить таблицу значений функции U, если “х” изменяется от 0 до p/2
c шагом p/4 и “y“ изменяется от 0 до 1 c шагом 0,4
U= 
9. Вычислить сумму вида: 
Получить результат при n= 10, m=15.
10. Получить таблицу значений функции U, при изменении “х” от 1 до 3 с шагом 1 и при изменении “y” от 0,5 до 2 с шагом 0,75
U= 
11.Получить таблицу значений функции U, при изменении “х” от -2 до -1 с шагом 0,5 и при изменении “y” от -1 до 0,6 с шагом 0,8
U= 
12. Вычислить сумму вида: 
Получить результат при n=10.
13. Высота прямой призмы, в основании которой лежит правильный шестиугольник,
изменяется от 2 до 10 см с шагом 4 см, а сторона шестиугольника – от 2 до 1 см
шагом 0,4 см. Получить таблицу изменения объема призмы V.
14. Вычислить все возможные значения функции: V=cos(nx+p)×sin(nx-p),
где p=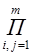 
; n=1,2,…k; x=0,5 Получить результат при k=10;m=20.
15. Вывести на печать каждый член последовательности f0, f1, f2,…fn, где
fi = 
Получить результат при n=10.
16. Получить таблицу значений функции y и найти уmax , если “х” изменяется от
-1 до 1 с шагом 0,4; а “z” изменяется от 0 до p/12 с шагом p/12.
y= 
17. Вычислить сумму положительных и сумму отрицательных значений функции Z
при изменении “x” от 0,2 до 1 с шагом 0,2 и при изменении “y” от –2 до 1
с шагом 0,5. Z=x2y3+siny×ln 
18. Дано натуральное число n. Найти тройку x, y, z таких натуральных чисел, что
n=x2+y2+z2 Получить результат при n=234.
19.. Получить таблицу значений функции U, найти Umin. Переменная “x”
изменяется от –1 до 0,6 с шагом 0,8: переменная “y” изменяется от 0 до 0,6 с
шагом 0,2.
U= 
; Z=max 
20. Получить таблицу значений функции U, при изменении “х” от 0 до 4
с шагом 2 и при изменении “y” от -5 до 3 с шагом 2.
U= 
; S= 
21.. Вычислить сумму вида: 
Получить результат при n=50, m=25.
22. Получить таблицу значений функции Z=cosx × 
, найти Zmin.
Переменная “x” изменяется от 0,1 до 0,95 с шагом 0,4;
“y” изменяется от 1,2 до 2,7 с шагом 1,5;
“t” изменяется от 0,7 до 1,7 с шагом 1.
23.. Вычислить сумму вида: sin(i3 + j4) Получить результат при n=50, m=30.
24. Получить таблицу значений функции V= arctgx - 
, найти Vmin.
Переменная “x” изменяется от 0,1 до 0,5 с шагом 0,4;
“y” изменяется от 1,2 до 2,7 с шагом 1,5;
“t” изменяется от 0,7 до 2,7 с шагом 1.
25. Дано натуральное число n. Найти тройки x, y, z таких натуральных чисел, что
n=x2+y2+z2 Получить результат при n=166
26. Вычислить сумму вида: 
Получить результат при n=50, m=50
27. Известно, что любое натуральное число можно представить в виде суммы не
более чем четырех квадратов неотрицательных целых чисел. Найти такие
неотрицательные целые числа x, y, z, t, что
n=x2+y2+z2+t2 Получить результат при n=421.
28 Вычислить сумму вида: k(k+1)×…×k2 Получить результат при n=4
29. Вычислить сумму вида: 
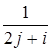Получить результат при n=50.
30. Вычислить сумму вида: 
Получить результат при x=5,2, n=30.
