Задача. Первый и второй игроки одновременно и независимо друг от друга показывают один, два или три пальца. Выигрыш или проигрыш (в денежных единицах) равен общему количеству показанных пальцев. Если это количество четное, то выигрывает первый игрок, а второй ему платит. Если же оно нечетное, то выигрывает второй игрок, а первый ему платит. Найти оптимальные стратегии каждого игрока.
Экономико-математическая модель
У каждого игрока имеется по три стратегии: показать один, два или три пальца. В соответствии с этим платежная матрица будет выглядеть следующим образом:
Выберем минимальные значения в каждой строке, а затем из них найдем максимальное. Это даст нам нижнюю цену игры. Она равна -3. Выберем максимальные значения в каждом столбце, а затем из них найдем минимальное. Получим верхнюю цену игры. Она равна 4. Так как нижняя цена игры не совпадает с верхней, то решение будем искать в смешанных стратегиях. Прибавляя ко всем элементам матрицы число, равное 5, перейдем к матрицы модифицированной игры:
,
которой соответствует задача линейного программирования для 1 игрока:
min f (x 1, x 2, x 3) = x 1+ x 2+ x 3
и задача линейного программирования для 2 игрока:
max f (x 1, x 2, x 3) = x 1+ x 2+ x 3
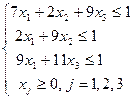
Решение.
Воспользовавшись симплексным методом, получим решения обеих задач, как описано ранее. Результаты приведены на рисунке.
Таким образом, оптимальная смешанная стратегия 1-го игрока совпадает с оптимальной смешанной стратегией 2-го игрока и равна (0,25;0,5;0,25).
Задачи для самостоятельного решения
1. Найти оптимальную стратегию 1-го игрока для игры двух участников с нулевой суммой путем сведения ее к задаче линейного программирования, если задана платежная матрица:
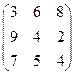
2. Найти оптимальную стратегию 2-го игрока для игры двух участников с нулевой суммой путем сведения ее к задаче линейного программирования, если задана платежная матрица:
3. Найти оптимальные стратегии игроков для игры двух участников с нулевой суммой, если задана платежная матрица:
4. Найдите оптимальные стратегии игроков в известной игре «камень, ножницы, бумага».
Лабораторная работа № 6. Динамическое программирование
Задача. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S 0=5 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k –му предприятию (k =1, 2, 3, 4), приносит в конце года прибыль fk (X). Функции fk (X) заданы таблично:
| Х | f 1(X) | f 2(X) | f 3(X) | f 4(X) |
Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.
Решение.
Обозначим через Xk количество средств, выделенных k -му предприятию. Суммарная прибыль равна 
. Переменные X удовлетворяют ограничениям: 
Требуется найти переменные X 1, X 2, X 3, X 4, удовлетворяющие данным ограничениям и обращающие в максимум функцию Z.
Рассмотрим особенности модели. Ограничения линейные, но переменные целочисленные, а функции fk (Xk) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств S 0=5 можно рассматривать как 4-шаговый, номер шага совпадает с номером предприятия; выбор переменных X 1, X 2, X 3, X 4 – уравнения соответственно на I, II, III, IV шагах; Ŝ - конечное состояние процесса распределения – равно нулю, так как все средства должны быть вложены в производство, Ŝ =0. Покажем схему распределения:
Уравнения состояний в данной задаче имеют вид:
 |
Sk = Sk -1- X, (k=
),
где Sk -параметр состояния – количество средств, оставшихся после k -го шага, т.е. средства, которые остается распределить между оставшимися (4- k) предприятиями.
Введем в рассмотрение функцию Zk * (Sk -1) – условно оптимальную прибыль, полученную от k -го, (k +1)-го,..., 4-го предприятий, если между ними распределялись оптимальным образом средства Sk -1 (0 £ Sk -1 £ 5). уравнения на k -ом шаге удовлетворяют условию: 0 £ Xk £ Sk -1 (либо k -му предприятию ничего не выделяем, Xk =0, либо не больше того, что имеем к k -му шагу, Xk £ Sk -1 ).
Последовательно решаем уравнения
проводя последовательную оптимизацию каждого шага. Для этого поступим следующим образом.
1. Создадим текстовую форму – таблицу для ввода условий задачи. Введем исходные данные задачи в созданную форму-таблицу:
2. В ячейку E15 введем формулу
=ИНДЕКС($B$3:$F$8; ПОИСКПОЗ($C15;$B$3:$B$8); G$12+1), скопируем формулу с ячейки E15 до ячейки Е35.
3. В ячейку F15 введем формулу
=ИНДЕКС($B$3:$F$8;ПОИСКПОЗ($D15;$B$3:$B$8);5), скопируем формулу с ячейки F15 до ячейки F35.
4. В ячейку G15 введем формулу =E15+F15, скопируем формулу с ячейки G15 до ячейки G35.
5. Находим максимальное значение для каждого состояния от 0 до 5, для этого в ячейку Н15 введем формулу =МАКС(G15), после копирования формулы в ячейку H16, необходимо изменить диапазон с G16 на G16:G17, для этого стоя в строке формул необходимо растянуть выделенный прямоугольник на одну ячейку вниз. Затем копируем формулу из H16 в ячейку H18 и проводим такие же операции по увеличению диапазона, и т.д. до ячейки H30.
6. Находим значение управления Хk, которому соответствует максимальное значение функции Z k, для этого в ячейку I15 введем формулу =ИНДЕКС($C15:G15;ПОИСКПОЗ(H15;G15;0);1), скопируем формулу в ячейки I16, I18, I21, I25, I30 постепенно увеличивая диапазон, аналогично тому, как это делалось в пункте 5. В результате получим следующую таблицу:
7. Выделяем диапазон ячеек E15:I35 выполняем команду Копировать, устанавливаем курсор в ячейку J15 выполняем команду Вставить.
8. Изменим формулу функции Z 3*(S 2). В ячейки K15, K16, K18, K21, K25, K30, введем соответственно максимальные значения предыдущего шага, находящиеся в ячейках H15, H16, H18, H21, H25, H30. В остальные ячейки поместим значения, стоящие в этом же столбце и соответствующие предыдущим Sk. В ячейку K17 копируем значение ячейки K15; в ячейки K19 и K20 – значения K16 и K17; в K22:K24 – K18:K20 и т. д. до ячейки K35. В результате получим:
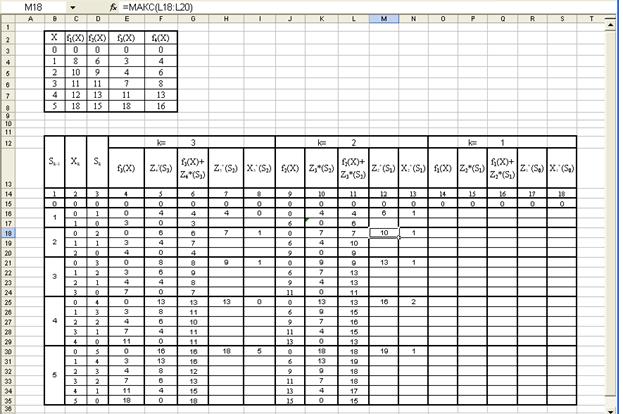
9. Выделяем диапазон ячеек J15:N35 выполняем команду Копировать, устанавливаем курсор в ячейку O15 выполняем команду Вставить. В результате получаем заполненную таблицу:
10. Сравнивая полученные значения, получим Z 1*(5)=24 усл. ед. = Zmax при X 1*= X 1*(5)=1. Вычисляя, получим S 1* = 5 - 1 = 4, а по таблице в столбце 12 находим X 2* = X 2* (4) = 2. Далее находим S 2* = 4-2 = 2, а в столбце 6 X 3* = X 3*(2) = 1. Наконец, S 3* = 2-1 = 1 и X 4* = X 4*(1) = 1, т. е. X *(1; 2; 1; 1).
Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию – 2 усл. ед.; 3-му предприятию – 1 усл. ед.; 4-му предприятию – 1 усл. ед.
