Моделирование преобразователя кода

Преобразователи кодов находят широкое применение в аппа­ратуре передачи данных для защиты передаваемой информа­ции от ошибок, а также для аппаратного шифрования каких-либо сведений. Преобразователем кода называется цифровой узел с m входами и n выходами, преобразующий один параллельный код в другой. Моделирование преобразова­теля кода имеет своей целью выполнить проверку синтезиро­ванной схемы на предмет соответствия таблицы истинности преобразованного кода с сигналами на выходах моделируемой схемы. Ниже описываются особенности моделирования уже синтезирован­ного преобразователя кода 8-4-2-1 в дополнительный код.

Задание 3

1. Создав новый файл, выполните графический ввод схемы преобразователя кода, осуществляющего преоб­разование входного сигнала по следующим выражениям для переменных Y2, Y1, Y0:

Входной код задан следующей таблицей (код 8—4—2—1).

Таблица 2-5.

Код 8-4-2-1

Х2	X1	Х0

Из анализа выражений и таблицы видно, что в качест­ве входных используются три сигнала Х0, X1 и Х2. Поэтому в схеме необходимо будет использовать три источника сигнала с различной частотой следования импульсов.

Для создания таких сигналов введите в схему три компонента DigClock (библиотека SOURCE.slb). Задайте для первого источника сигнала Х0 параметры ONTIME (длительность импульса) = 0,5 мкс и OFFTIME (дли­тельность паузы) = 0,5 мкс. Аналогичным образом вве­дите в схему и задайте параметры источников сигна­лов X1 (ONTIME = 1 мкс и OFFTIME = 1 мкс) и Х2 (ONTIME = 2 мкс и OFFTIME = 2 мкс). На рис. 2-23 показаны временные диаграммы сигналов Х0, X1, Х2.

2. Для реализации логического выражения, в соответс­твии с которым осуществляется преобразование кода, не­обходимо ввести логические элементы и соответствующим образом выполнить соединения. Из анализа выражения Y2 видно, что для схемной реализации такой логической опе­рации необходимо использовать следующие элементы:

- двухвходовый элемент И-НЕ для операций , (компонент 7400);

- трехвходовый элемент И-НЕ для результирующей операции (компонент 7410).

Введем последовательно такие компоненты и выполним соответствующие соединения. Для реализации логической операции необходимо ввести два компонента 7400.

Для этого нажмите кнопку выбора компонентов и в раскрыв­шемся окне Part Browser Basic кнопку Libraries (библиотеки), в поле Library выберите библиотеку EVAL.slb, а в поле Part — компонент 7400, после чего нажмите кнопки ОК, затем Place & Close (ввести компонент и закрыть диалоговое окно).

Рис. 2-23. Временные диаграммы сигналов Х0, X1, Х2

Соединим выход источника сигнала Х0 с входа­ми компонента D4A (в результате на выходе получим значение , выход которого и сигнал Х2 необходимо

завести на входы компонента D1A. Позици­онные обозначения логических элементов могут отли­чаться от приводимых, что связано с после­довательностью ввода и размещением на схеме самих элементов.

Затем выполним ввод еще двух компонентов и необходимые соединения для реализации операции : соединим выход источника сигнала Х2 с входами компонента D5A, выход которого и сигнал Х0 необходимо завести на входы компонента D3A. Для реализации последней опе­рации (объединение по трем входам с отрицанием) введем компонент 7410 (получит имя D6A). Соединим входы компонента D2A с сигналом X1 (получим ) выходы D1A, D2A, D3A с входами D6A. Получим фрагмент схемы, реализующий выходную переменную Y2 в соответствии с заданным выражением .

Рис. 2-24. Схема, обеспечивающая реализацию логического выражения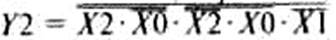

Аналогичным образом введите компоненты и выпол­ните необходимые соединения для реализации выходных переменных Y1, Y0.

3. Для удобства анализа результатов моделирования обозначьте выходы источников сигналов как Х2, X1, Х0, а выходы компонентов, реализующих схемные функции, как Y2, Y1, Y0. Для этого дважды нажмите на соответствующем проводнике, исходящем от компонента, и в появившемся
диалоговом окне введите соответствующее обозначение.

4. Расположите на обозначенных проводниках Х2, X1, Х0 и Y2, Y1, Y0 маркеры для измерения сигналов, исполь­зуя команду Markers/Mark Voltage и расставляя маркеры в указанной последовательности.

5. Сохраните схему.

Задайте необходимые параметры директивы модели­рования переходных процессов(Analysis Setup/Transient): конечное время анализа (Final Time = 20u), временной шаг расчета характеристик (Step Ceiling = 50n) и интервал между точками отсчета при выводе результатов модели­рования (Print Step = 50n). Закрыв окно Analysis Setup, запустите режим моделирования командой Analysis/Simu­late или нажатием клавиши F11.

Рис. 2-25. Схема преобразователя кода 8-4-2-1 в дополни­тельный код

 

7. В окне программы Probe по графикам входного и преобразованного кодов проверьте соответствие по­лученных результатов и таблицы истинности (табли­ца 2-6). Для этого, включите режим привязки курсора к построенному графику (кнопка ), щелкните левой кнопкой мыши на графике и в дискретные моменты времени, соответствующие изменению входных пере­менных Х2, X1, Х0,определите значения выходных пе­ременных Y2, Y1, Y0.

Для проверки работоспособности схемы преобразо­вателя кода приводится таблица истинности первичного и преобразованного кодов.

Таблица 4.6.

Таблица соответствия кода 8-4-2-1 и дополнительного кода

Код 8-4-2-1	Дополнительный код
х2	x1	х0	у2	y1	у0

В рассмотренном примере использованы простейшие ло­гические элементы, при этом возможно моделирование циф­ровых схем в другом элементном базисе, что определяется со­ставом библиотек цифровых компонентов системы DesignLab.