Перед началом измерений следует ознакомиться с работой генератора сигналов и электронного осциллографа.
Задание 1. Изучение дифференцирующей цепи и измерение зависимости постоянной времени от сопротивления.
1. Соберите цепь согласно схеме, приведенной на рис. 4.9.
2. Установите тумблер Т в положение П1.
3. Зарисуйте наблюдаемую осциллограмму напряжения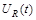 
, снимаемую с сопротивления 
(подключение к точкам «3» и «4»).
4. По осциллограмме определите значение 
и 7–10 значений 
, соответствующих моментам времени 
(точки следует брать в наиболее искривленных участках осциллограммы). Заполните таблицу 4.2.
Таблица 4.2
| № п/п | , В
| , мс
| , В
| 
| 
|
5. Постройте график зависимости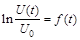 
от времени.
6. По полученному графику с использованием формулы (4.27) рассчитайте величину 
.
7. Отключите питание от платы и, подключив между клеммами «3» и «4» омметр, измерьте сопротивление .
8. Полученные значения и занесите в таблицу 4.3.
Таблица 4.3
| № п/п | , Ом
| , мс
|
9. Изменяя значения в сторону уменьшения и увеличения , проведите измерения по п.п. 3–9 для 7–10 различных сопротивлений.
10. По данным таблицы 4.3 постройте график зависимости 
. Проверить справедливость формулы (4.8).
Задание 2. Изучение интегрирующей цепи и измерение зависимости постоянной времени от сопротивления.
1. Соберите цепь согласно схеме, приведенной на рис. 4.10.
2. Установите тумблер Т в положение П2.
3. Для новой цепи выполните пункты 3–10, описанные в задании 1, с учетом того, что теперь на экране осциллографа будут осциллограммы напряжений 
, снимаемых с конденсатора (подключение к точкам «4» и «5»).
Контрольные вопросы
1. Что такое 
-цепи? Нарисуйте простейшую -цепь.
2. Что такое релаксационный процесс в электрических цепях?
3. Работа -цепи (установление тока) в режиме замыкания и размыкания.
4. График зависимости силы тока и напряжения от времени при релаксационных процессах.
5. Что такое постоянная времени -цепи? Нарисовать графики зависимостей 
и 
для различных .
6. Сформулируйте законы Кирхгофа.
7. Какая цепь называется переходной? При каких условиях?
8. Какая цепь называется дифференцирующей (интегрирующей) и почему? Нарисуйте и объясните графики процессов.
9. Объясните работу экспериментальной установки.
10. Рассказать о методике определения постоянной времени релаксации.
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ ОТНОСИТЕЛЬНОЙ ДИЭЛЕКТРИЧЕСКОЙ
ПРОНИЦАЕМОСТИ МАТЕРИАЛОВ
Цель работы: определение диэлектрической проницаемости материалов по измерению емкости плоского конденсатора.
Приборы и материалы: электронный осциллограф, звуковой генератор, универсальный лабораторный стенд, сменная плата с макетом лабораторной работы, набор диэлектрических пластинок.
Краткая теория
Емкость плоского конденсатора в системе СИ, как известно, вычисляется по формуле:
, (5.1)
где 
=8,85×10-12 Ф/м – абсолютная диэлектрическая проницаемость вакуума, 
– относительная диэлектрическая проницаемость материала, 
– площадь обкладок плоского конденсатора, 
– расстояние между обкладками плоского конденсатора.
Зная геометрию конденсатора (т. е. площадь обкладок и расстояние между ними) и измерив его емкость, можно вычислить относительную проницаемость по формуле:
. (5.2)
В настоящей работе емкость конденсатора вычисляется по проводимости на переменном токе в схеме, приведенной на рис. 5.1.
Коэффициентом передачи 
называется отношение амплитуды напряжения на выходе к амплитуде напряжения на входе. В приложении 2 показано, что в представленной цепи коэффициент передачи равен:
. (5.3)
Отсюда емкость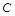 
может быть определена по формуле:
. (5.4)
Таким образом, измеряя амплитуды входного и выходного напряжения и определяя по их отношению коэффициент передачи , можно вычислить емкость плоского конденсатора по формуле (5.4).
