ИЗУЧЕНИЕ РЕЛЕКСАЦИОННЫХ ПРОЦЕССОВ В RC-ЦЕПИ
Цель работы: изучение зависимости тока и напряжения от времени в цепях, содержащих RC-элементы.
Приборы и материалы: универсальный лабораторный стенд, осциллограф, омметр, сменная плата, соединительные провода со штекерами.
Краткая теория
Теория релаксационного процесса в RC-цепи
RC-цепью называют цепь, содержащую конденсатор и резисторное сопротивление. Под релаксационным процессом в RC-цепях понимается процесс установления стационарного заряда конденсатора при подаче на него напряжения.
Для анализа процесса рассмотрим цепь, приведенную на рис. 4.1.
Пусть конденсатор 
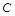предварительно заряжен зарядом 
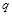, как показано на рис. 4.1. После замыкания ключа 
конденсатор начнет разряжаться током 
, протекающим через резистор 
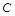. Поскольку емкость и резистор включены параллельно, напряжение на них одно и то же:
. (4.1)
Так как 
и 
, то из (4.1) получаем:
. (4.2)
Ток в цепи пропорционален заряду конденсатора 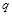. Опираясь на этот факт, можно найти зависимость заряда конденсатора от времени. С течением времени заряд конденсатора уменьшается до нуля, причем скорость уменьшения заряда равна силе тока через конденсатор:
. (4.3)
Пусть время, за которое заряд конденсатора уменьшится в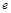 
раз, равно 
. Обозначим за 
значение тока в цепи в момент времени , а 
– заряд конденсатора в тот же момент времени. Тогда для момента времени имеем уравнение:
. (4.4)
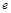Это уравнение, с точностью до обозначений, совпадает с уравнением (4.2), поэтому заряд уменьшится в раз через тот же промежуток времени . Продолжая рассуждения, по аналогии можно составить такую таблицу:
Таблица 4.1
|
| 2
| ... | 
| |
|
| 
| 
| ... | 
|
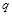
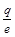
Из таблицы можно заключить, что зависимость заряда конденсатора от времени должна иметь вид:
. (4.5)
Значение 
, очевидно, равно заряду конденсатора в момент времени 
, т.е. немедленно после замыкания ключа .
В справедливости полученной формулы легко убедиться, если из уравнения (4.2) исключить силу тока с помощью уравнения (4.3). Уравнение для заряда будет выглядеть так:
. (4.6)
Подставляя из уравнения (4.5), получим:
. (4.7)
Отсюда следует, что уравнения (4.7) и (4.6) удовлетворяются, если:
. (4.8)
Величина называется постоянной времени 
-цепи.
Зная заряд на конденсаторе, легко найти напряжение на нем, поделив заряд конденсатора на величину его емкости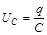 
.
Напряжение на конденсаторе меняется по закону:
, (4.9)
где 
– значение напряжения на конденсаторе при .
Поделив напряжение на величину резисторного сопротивления, можно найти зависимость тока в цепи от времени:
. (4.10)
Графики зависимостей силы тока и напряжения от времени приведены на рис. 4.2 и рис. 4.3.
 |
|
Пусть до замыкания ключа конденсатор не заряжен. После замыкания ключа в момент времени в цепи возникает ток , и конденсатор начинает заряжаться. При этом для контура выполняется второй закон Кирхгофа:
. (4.11)
Заменив и , получаем:
. (4.12)
Так как сила тока равна скорости увеличения заряда конденсатора:
, (4.13)
то, дифференцируя (4.12) и подставляя из (4.13), получаем:
. (4.14)
Уравнение (4.14) совпадает с точностью до замены 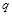на с уравнением (4.6). Поэтому решение уравнения (4.14) можно написать по аналогии с решением уравнения (4.6):
, (4.15)
где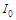 
– значение тока в начальный момент времени, которое можно определить из уравнения (4.11), учитывая, что 
при . Тогда:
, (4.16)
а напряжение на резисторе меняется по закону:
. (4.17)
Напряжение на емкости можно найти из (4.11) и (4.17):
. (4.18)
Графики этих зависимостей приведены на рис. 4.5 и рис. 4.6.
Методика выполнения работы
