8.1 Цель работы:
8.1.1 Составление программ циклических алгоритмов (Цикл с предусловием, с постусловием, с параметром).
8.1.2 Отладка программы и контрольный просчет.
Приборы и оборудование
8.2.1 Free Pascal
8.2.2 ПЭВМ IBM PC/XT
8.2.3 Microsoft Word
8.2.4 Задание на выполнение работы в электронном варианте.
Порядок выполнения работы
8.3.1 Выберите номер варианта, согласно списка в учебном журнале (Приложение А).
8.3.2 Составьте программу, используя язык программирования Free Pascal.
8.3.3 Составьте программу, используя команды цикла (Цикл с предусловием, с постусловием, с параметром).
8.3.4 Отладить программу с использованием контрольного примера (значения переменных задайте сами).
8.3.5 Результаты работы распечатайте на принтере.
8.3.6 Оформите лабораторную работу для сдачи преподавателю.
8.3.7 Ответьте на контрольные вопросы устно
Примечание: На одном примере использовать по возможности все три цикла в одной программе и задать одни и те же значения для переменных, чтобы проверить результаты работы этих циклов и их различие.
Контрольные вопросы
8.4.1 В чем различие трех операторов цикла?
8.4.2 Когда нельзя использовать оператор FOR.
8.4.3 Чем отличаются операторы ДО и ПОКА друг от друга? Как записывается и как работает оператор FOR?
8.4.4 Для организации каких циклов применим оператор FOR?
8.4.5 В чем отличие оператора WHILE от оператора REPEAT?
8.4.6 Как программируются циклические алгоритмы с явно заданным числом повторений цикла?
8.4.7 Как программируются циклические алгоритмы с заранее неизвестным числом повторений цикла?
8.4.8 Напишите оператор цикла, который не выполняется ни разу.
8.4.9 Напишите оператор цикла, который выполняется неограниченное число раз.
8.4.10 Замените оператор "Repeat A Until B" равносильным фрагментом программы с оператором While.
Приложение А
| Номер варианта | Задание |
| 1.1 Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9. 1.2 Дано натуральное число n. Найти сумму первой и последней цифры этого числа 1.3 Составить программу для сравнения двух n- значных чисел (n>20) | |
| 2.1 Найти все трехзначные числа, сумма цифр которых равна данному целому числу. 2.2 Дано натуральное число n. Переставить местами первую и последнюю цифры этого числа 2.3 Составить программу, суммирующую два натуральных n- значных числа, где n>20 | |
| 3.1 Найти все трехзначные числа, средняя цифра которых равна сумме первой и третьей цифр 3.2 Дано два натуральных числа m иn. (m<=9999, n<=9999). Проверить, есть ли в записи числа m цифры, совпадающие с цифрами числа n 3.3 Составить программу для вычисления степеней чисел вида аn, если a>MaxInt, n>10 | |
| 4.1 Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры. 4.2 Дано натуральное число n. Проверить, есть ли в записи числа три одинаковые цифры (n<=9999) 4.3 Составить программу для вычисления 264-1, в результате сохранить все цифры | |
| 5.1 Найти все двузначные числа, сумма квадратов цифр которых делится на 17 5.2 Дано натуральное число n<=9. Дописать к нему цифру к в конец и в начало 5.3 Составить программу для вычисления 100! | |
| 6.1 Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр 6.2 Дано натуральные числа n, к. Проверить, есть ли в записи числа nk цифра m 6.3 Вычислить 100!+2100 | |
| 7.1 Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа 7.2 Среди всех n – значных чисел указать те, сумма цифр которых равна данному числу k 7.3 Вычислить 100!-2100 | |
| 8.1 Найти двузначное число, равное утроенному произведению его цифр. 8.2 Заданы три натуральных числа A,B,С, которые обозначают число, месяц и год. Найти порядковый номер даты, начиная отсчет с начала года. 8.3. Вычислить 7123 | |
| 9.1 В каких двузначных числах удвоенная сумма цифр равна их произведению? 9.2 Найти наибольшую и наименьшую цифры в записи данного натурального числа 9.3 Вычислить 2-200 | |
| 10.1 Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи 10.2 Произведение n первых нечетных чисел равно p. Сколько сомножителей взято? Если введенное число n не является указанным произведением, сообщить об этом. 10.3 Найти количество делителей n- значного натурального числа (n>20) | |
| 1. 11.1 Даны два целых числа A и B (A < B). 2. Вывести все целые числа, расположенные между данными числами (не включая сами эти числа), в порядке их возрастания, а также количество N этих чисел. 11.2 Найти на отрезке [n,m] натуральное число, имеющее наибольшее количество делителей 11.3 Вычислить точное значение (n!)! (n>=4) | |
| 12.1 Даны два целых числа A и B (A < B). Вывести все целые числа, расположенные между данными числами (включая сами эти числа), в порядке их убывания, а также количество N этих чисел 12.2 Задумано некоторое число x (x<100). Известны числа k,m,n- остатки от деления этого числа на 3,5,7. Найти x. 12.3 Составить программу для вычисления точного значения суммы 1!+2!+…+n! При n>10 | |
| 3. 13.1 Дано вещественное число A и целое число N (> 0). 4. Вывести A в степени N: AN = A·A·...·A (числа A перемножаются N раз). 13.2 Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N-1, у которых сумма всех цифр совпадает с суммой цифр данного числа. Если таких чисел нет, то вывести слово «нет». Пример. N=44. Числа:17, 26, 35 13.3 Составить программу для вычисления точного значения суммы дробей 1/1!+1/2!+…+1/n! При n>10. Ответ должен быть представлен в виде несократимой дроби p/q,где p,q- натуральные числа | |
| 5. 14.1 Дано вещественное число A и целое число N (> 0). 6. Вывести все целые степени числа A от 1 до N. 14.2 Дано натуральное число n. Найти и вывести все числа в интервале от 1 до N-1, у которых произведение всех цифр совпадает с суммой цифр данного числа. Если таких чисел нет, то вывести слово «нет». Пример. N=44. Числа:18, 24 14.3 Вычислить точное значение (nn)! (n>=3) | |
| 7. 15.1 Дано вещественное число A и целое число N (> 0). 8. Вывести 1 + A + A2 + A3 +... + AN. 15.2 Дано натуральное число n. Определить количество 8-значных чисел, у которых сумма цифр в цифровой записи числа больше, чем N. Если таких чисел нет, то вывести слово «нет». 15.3 Составить программу для вычисления точного значения суммы первых n членов последовательности 1, к, к2, к3,.., к n (n>MaxInt) | |
| 9. 16.1 Дано вещественное число A и целое число N (> 0). 10. Вывести 1 - A + A2 - A3 +... + (-1)NAN. 16.2 Дано натуральное число n. Найти наибольшее число M (M>1), на которое сумма цифр в цифровой записи числа N делится без остатка. Если таких чисел нет, то вывести слово «нет». Пример. N=12345, M=5. Сумма цифр числа N, равная 15, делится на 5 16.3 Вычислить точное значение суммы 12+22+32+..+n2 (n>=20000) | |
| 17.1 Дано целое число N (> 1). Вывести наименьшее целое K, при котором выполняется неравенство 3K > N, и само значение 3K. 17.2 Дано натуральное число n. Найти наименьшее число M (N<M<=2*N), которое делится на сумму цифр числа N (без остатка). Если таких чисел нет, то вывести слово «нет». Пример. N=12345, M=12360. Число 12360 делится на число 15 – сумма цифр числа N 17.3 Вычислить точное значение суммы 1 n +2 n +3 n +..+n n (n>=10) | |
| 11. 18.1 Дано целое число N (> 1). 12. Вывести наибольшее целое K, при котором выполняется неравенство 3K < N, и само значение 3K. 18.2 Дано натуральное число N (N>9). Определить количество нулей, идущих подряд в младших разрядах данного числа. Пример. N=1100000. Количество нулей равно четырем 18.3 Вычислить 200!+3100 | |
| 19.1 Дано вещественное число A (> 1). Вывести наименьшее из целых чисел N, для которых сумма 1 + 1/2 +... + 1/N будет больше A, и саму эту сумму 19.2 Дано натуральное число N (N>9). Определить количество нулей в цифровой записи числа, кроме нулей в младших разрядах. Пример. N=10025000. Количество нулей равно двум 19.3 Вычислить 200!-3100 | |
| 13.20.1 Дано вещественное число A (> 1). 14.Вывести наибольшее из целых чисел N, для которых сумма 1 + 1/2 +... + 1/N будет меньше A, и саму эту сумму. 20.2 Дано натуральное число N (N>9). Определить сумму цифр в первой половине числа (старшие разряды). Пример N=12345678. Сумма составляет 1+2+3+4=10 20.3 Вычислить 5123 | |
| 15. 21.1 Дано целое число N (> 0). Вывести произведение 1·2·...·N. 16. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число. 21.2 Дано натуральное число N (N>9). Определить сумму цифр во второй половине числа (младшие разряды). Пример N=12345678. Сумма составляет 5+6+7+8=26 21.3 Вычислить 3-200 | |
| 17. 22.1 Дано целое число N (> 0). Если N - нечетное, то вывести произведение 1·3·...·N; если N - четное, то вывести произведение 2·4·...·N. 18. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число. 22.2 Дано натуральное число n. Если число содержит 3 цифры, то получить новое число M, которое образуется путем перестановки первой и последней цифр данного числа. Если количество цифр не 3, то M=N. Пример N=123 M=321 22.3 Вычислить 500!+4100 | |
| 19. 23.1 Дано целое число N (> 2) и две вещественные точки на числовой оси: A, B (A < B). 20. Отрезок [A, B] разбит на равные отрезки длины H с концами в N точках вида A, A + H, A + 2H, A + 3H,..., B. 21. Вывести значение H и набор из N точек, образующий разбиение отрезка [A, B]. 23.2 Дано натуральное число n. Если число содержит 5 цифры, то получить новое число M, которое образуется путем исключения средней цифры данного числа. Если количество цифр не 5, то M=N. Пример N=12345 M=1245 23.3 Вычислить 500!-4100 | |
| 22. 24.1 Дано целое число N (> 2) и две вещественные точки на числовой оси: A, B (A < B). 23. Функция F(X) задана формулой F(X) = 1 - sin(X). 24. Вывести значения функции F в N равноотстоящих точках, образующих разбиение отрезка [A, B]: F(A), F(A + H), F(A + 2H),..., F(B). 24.2 Дано натуральное число n. Среди чисел 1,…., n найти такие, запись которых совпадает с последними цифрами записи их квадратов (например, 62=36, 252=5625) 24.3 Вычислить 8123 | |
| 25.1 Дано число D (> 0). Последовательность чисел AN определяется следующим образом: A1 = 2, AN = 2 + 1/AN-1, N = 2, 3,... Найти первый из номеров K, для которых выполняется условие |AK - AK-1| < D, и вывести этот номер, а также числа AK-1 и AK 25.2 Дано натуральное число n. Найти все делители числа n. 25.3 Вычислить 3-200 | |
| 26.1 Дано число D (> 0). Последовательность чисел AN определяется следующим образом: A1 = 1, A2 = 2, AN = (AN-2+ AN-1)/2, N = 3, 4,... Найти первый из номеров K, для которых выполняется условие |AK AK-1| < D, и вывести этот номер, а также числа AK-1 и AK 26.2 Дано целое число n>2. Напечатать все простые числа из диапазона [2,n] 26.3 Вычислить 900!+2100 | |
| 27.1 Определить, является ли заданное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3). 27.2 Даны натуральные числа n,m. Найти все натуральные числа <n, квадрат суммы цифр которых равен m 27.3 Вычислить 900!-2100 | |
28.1 Вычислить сумму и произведение: z= 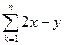 z1= z1=  28.2 Даны натуральные числа n,m. Получить все делители числа n, взаимно простые с m
28.3 Вычислить 9123
28.2 Даны натуральные числа n,m. Получить все делители числа n, взаимно простые с m
28.3 Вычислить 9123
| |
29.1 Вычислить сумму и произведение: z=  z1=
z1=  29.2 Дано натуральное число n. Определить количество цифр в цифровой записи данного числа, которые имеют наибольшее значение. Пример N=1808. Количество равно двум (две цифры 4)
29.3. Вычислить 4-200
29.2 Дано натуральное число n. Определить количество цифр в цифровой записи данного числа, которые имеют наибольшее значение. Пример N=1808. Количество равно двум (две цифры 4)
29.3. Вычислить 4-200
| |
30.1 Вычислить сумму и произведение: z=  z1= z1=  30.2 Дано натуральное число n. Определить количество цифр в цифровой записи данного числа, которые имеют наименьшее значение. Пример N=4548. Количество равно двум (две цифры 8)
30.3 Вычислить точное значение (nn)! (n>=5)
30.2 Дано натуральное число n. Определить количество цифр в цифровой записи данного числа, которые имеют наименьшее значение. Пример N=4548. Количество равно двум (две цифры 8)
30.3 Вычислить точное значение (nn)! (n>=5)
|






