Пусть получена выборка из двумерной совокупности при наблюдении двух случайных величин X и Y (табл.1.1).
Таблица 1.1
| i | 1 | 2 | 3 | … | i | … | N |
| X | x1 | x2 | x3 | … | xi | … | xN |
| Y | y1 | y2 | y3 | … | yi | … | yN |
Обработку результатов наблюдений в данном случае проводят по следующей схеме:
1) Построение поля рассеяния, как правило, первый шаг при обработке результатов наблюдений двумерной совокупности случайных величин X и Y; для этого на плоскости с координатами x, y отмечают экспериментальные точки (см. рис.).
2) Составление таблицы двумерного распределения. Эту таблицу составляют следующим образом:
- Оси Оx и Оy разбивают на отдельные интервалы длиной Dx и Dy. Величины Dx, Dy, количество Kx, Ky и размещение этих интервалов для каждой из переменных X и Y находят с помощью правил (1.17 – 1.19);
- соответствующие границы наносят на диаграмму рассеяния и затем подсчитывают количество точек Nm1, m2 , попавших в каждый из образовавшихся прямоугольников (при условии, что если какая-либо точка расположена на границе, то ее относят к правому или верхнему прямоугольнику);
- далее составляют таблицу (табл. 1.2);
Таблица 1.2
| Интервалы: x/y | [y1, y1 + Dy) | [y2, y2 + Dy) | … | [ym2, ym2 + Dy) | … | [yk2, yk2 + Dy) |
| [x1, x1 + Dx) | ... | |||||
| 1/40 | ||||||
| [x2, x2 + Dx) | … | |||||
| … | … | … | … | … | … | … |
| [xm1, xm1 + Dx) | … | Nm1,m2 | ||||
| Nm1,m2/N | ||||||
| … | … | … | … | … | … | … |
| [xk1, xk2 + Dx) | … | |||||
| 1/40 | 1/40 |
- в этой таблице отмечают величины Nm1,m2, а так относительные величины Nm1,m2/N (ниже диагонали). Подобную таблицу можно использовать как исходную для построения гистограмм и диаграмм накопленных частот в трехмерном пространстве, которые являются эмпирическими аналогами двумерного интегрального закона и двумерной функции распределения. С помощью таблицы двумерного распределения легко получить исходные данные для построения гистограмм, соответствующих каждой из одномерных случайных величин X и Y. Для этого достаточно просуммировать значения таблицы либо по каждому столбцу (при построении гистограммы для Y), либо по каждой строке (при построении гистограммы для X).
3) Вычисление оценки коэффициента корреляции производят по формуле
= 
- 
)(
, (1.23)
где , 
, и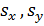 
находят с помощью формул (1.20…1.22).
Между значением и знаком коэффициента корреляции, с одной стороны и видом диаграммы рассеяния – с другой, существует определенная связь. Если начало координат принести в точку 
, ), то:
- при 
> 0 точки на диаграмме рассеяния группируются в основном в I и III квадрантах, а при < 0 – во II и IV;
- при 
» 0 точки беспорядочно разбросаны во всех четырех квадрантах;
- при = ± 1 точки группируются на прямых (находящихся либо в I и III квадрантах, либо во II и IV).
ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Исследовать свойства одномерной случайной величины:
- сформировать выборку из 25 значений;
- построить вариационный ряд;
- построить диаграмму накопленных частот;
- построить гистограмму;
- рассчитать оценки математического ожидания, дисперсии и среднего квадратического отклонения.
2. Исследовать свойства двумерной совокупности случайных величин:
- варьируя исходными данными получить три совокупности значений;
- по полученным данным построить три поля рассеяния;
- составить таблицы двумерных распределений;
- построить гистограммы,
- вычислить для всех трех случаев оценки коэффициента корреляции.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дать определение случайной величины.
2. Дать определение одномерного интегрального и дифференциального законов распределения случайной величины и назвать их свойства.
3. Дать определение двумерного интегрального и дифференциального законов распределения случайных величин и назвать их свойства.
4. Какие числовые характеристики наиболее используются в качестве мер расположения и рассеяния одномерной и двумерной совокупности случайных величин?
5. Каким образом производится построение вариационного ряда, диаграммы накопленных частот, гистограммы выборки одномерной случайной величины?
6. Каким образом производится построение поля рассеяния и составление таблицы распределения двумерной совокупности случайных величин?
7. Каков физический смысл коэффициента корреляции, в каких пределах он изменяется и что характеризует?
