Найти производную и дифференциал:
.
Решение: для нахождения производной данной функции используем два правила дифференцирования: 1) 
;
2) 
[справедливы следующие формулы: 
] 
.
Дифференциал функции ищем по формуле:
.
.
Ответ: 
;
Задание №3.
Найти 
-?
Решение: найдем 
от данной функции. Воспользуемся формулой:
.
.
Найдем 
.
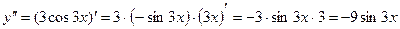Теперь найдем 
.
.
Ответ: 
.
Задание №4.
Доказать, что 
.
Для доказательства найдем производную в левой части равенства. Воспользуемся следующим правилом дифференцирования: , т.е. 
.
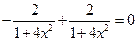Получим, что левая часть равна правой.
Что и следовало доказать.
Задание №5.
Точка совершает прямолинейное колебательное движение по закону 
, 
. Определить скорость и ускорение движения в момент времени 
.
Решение:
; 
Ответ: 
; 
.
