Многих переменных

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ

 

 

1. Частные производные

Пусть x=(x₁,x₂,…,x_m) – внутренняя точка области определения функции u=f(x₁,…,x_m). Рассмотрим частное приращение этой функции по переменной x_k .

 

Определение. Если существует предел отношения при , то этот предел называют частной производной функции f в точке 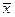по к-ой переменной и обозначают следующими символами . Таким образом .

Отметим, что частная производная функции f по аргументу x_k представляет собой обыкновенную производную функции одной переменной x_k при фиксированных значениях остальных переменных. Поэтому вычисления частных производных производится по обычным правилам вычисления производных функций одной переменной.

Заметим, что из существования у функции в данной точке всех частных производных, вообще говоря, не вытекает непрерывность функций в этой точке.

 

Задание. Привести пример такой функции.

 

2. Дифференцируемость функции многих переменных

 

Рассмотрим приращение (то есть полное приращение) функции u=f(x₁,…,x_m) в точке 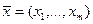, соответствующее приращениям аргументов .

 

Определение. Функция f называется дифференцируемой в точке 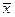, если её полное приращение в этой точке может быть представлено в виде , (1)

где A₁,A₂,…,A_m – числа, α₁,α₂,…,α_m – бесконечно малые при функции, равные 0 при .

 

Соотношение (1) называют условием дифференцируемости функции f в точке .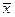

Его можно записать в другой форме. Рассмотрим функцию . Заметим, что при при любых i. Поэтому .Следовательно, (2)

Докажем, что из представления (2) вытекает представляет представление (1).

Действительно, .

Полагая и учитывая, что , мы придем к представлению (1). Итак, условия (1) и (2) эквивалентны.

Справедлива следующая теорема.

 

Теорема 1. Если функция f дифференцируема в точке 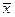, то в этой точке существуют частные производные по всем переменным, причем , где A_i – числа из условия (1) или (2).