Одним из наиболее убедительных подтверждений основ молекулярно-кинетической теории является броуновское движение. Это явление было открыто в 1827 году английским ботаником Броуном. Оно заключается в том, что все мельчайшие частицы, взвешенные в жидкости, находятся в непрерывном движении. Характер броуновского движения зависит от свойств жидкости и газа, в которых взвешены частицы, но не зависит от свойств вещества самих частиц. Скорость движения броуновских частиц возрастает с повышением температуры и с уменьшением размеров частиц. Все эти закономерности легко объяснить, если мы примем, что движения взвешенных частиц возникают вследствие ударов, испытываемых ими со стороны беспорядочно движущихся молекул жидкости или газа, в которых они находятся.
Броуновское движение объясняется тем, что благодаря хаотичному движению молекул, число ударов молекул на взвешенную частицу с разных сторон не будет одинаковым, в результате возникает некоторая равнодействующая сила определенного направления. Это приводит к движению броуновской частицы по направлению этой силы. Через короткий промежуток времени направление равнодействующей силы изменится и вместе с тем изменится направление движения частицы. Отсюда следует хаотичное движение броуновских частиц, отражающая хаотичность молекулярного движения. Вероятность возникновения равнодействующей силы, связанной ударами молекул о частицу тем больше, чем меньше размеры частиц.
Рассмотрим количественную теорию броуновского движения, созданную Эйнштейном и независимо Смолуховским.
Вследствие неполной компенсации ударов молекул на броуновскую частицу действует, как мы указали выше, некоторая результирующая сила 
, под действием которой и частица движется. Кроме этой силы на частицу действует сила трения 
, вызванная вязкостью среды и направленная против силы . Для простоты предположим, что броуновские частицы имеют форму сферы радиуса 
. Тогда сила трения может быть выражена формулой Стокса:
, (3.17)
где 
- коэффициент вязкости среды, 
- скорость движения частицы. Уравнение движения частицы запишется в виде:
. (3.18)
Здесь 
- масса частицы, 
- радиус-вектор относительно произвольной системы координат, 
- скорость частицы.
Рассмотрим проекцию радиус-вектора на ось Х. Для этой составляющей уравнение (3.18) перепишется в виде:
, (3.19)
где 
- проекция результирующей силы на ось Х.
Наша задача определить смещение 
броуновской частицы, которое она получит под действием ударов молекул. Различные частицы получают смещение, отличающиеся как по величине, так и по направлению. Вероятное значение суммы смещений всех частиц равно нулю, так как смещения с одинаковой вероятностью могут быть как положительными, так и отрицательными. Среднее значение смещения частиц 
также будет также равно нулю. Но не будет равно нулю среднее значение квадрата смещения 
. Преобразуем уравнение (3.19) так, чтобы в него входила величина . Для этого умножим обе части этого уравнения на :
. (3.20)
Используем очевидные тождества:
.
Поставив это выражение в (3.20), получим:
.
Это равенство для любой частицы и поэтому она справедлива также для средних значений входящих в него величин, если усреднение вести по достаточно большому числу частиц. Поэтому можно записать:
.
- среднее значение квадрата составляющей скорости частицы по оси Х. Для большого числа частиц 
и одинаково часто принимают как положительные, так и отрицательные значения, поэтому 
. Уравнение (3.19) примет вид:
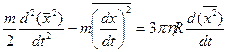. (3.21)
Так как движения частиц вполне хаотичны, средние значения квадратов составляющих скорости по всем трем координатным осям должны быть равны друг другу, т.е.
.
Очевидно, что
,
где 
- среднее значение квадрата скорости частицы, откуда следует
.
Таким образом, интересующее нас выражение, входящее в (3.21), равно:
,
где 
- средняя кинетическая энергия броуновской частицы.
Сталкиваясь с молекулами жидкости или газа, броуновские частицы обмениваются с ними энергией, и находятся в тепловом равновесии со средой, в которой они находятся. Поэтому средняя кинетическая энергия поступательного движения броуновской частицы должны быть равна средней кинетической энергии молекул жидкости или газа, которая равно, как известно, 
:
.
Следовательно
. (3.22)
Учитывая (3.22), уравнение (3.21) перепишется в виде:
. (3.23)
Это уравнение легко интегрируется. Обозначив 
, получим:
.
После разделения переменных, имеем:
.
Интегрируя левую часть этого уравнения в пределах от 0 до z, а правую от 0 до t, получим:
.
Или
.
Отсюда
.
Из этого выражения получим, что
.
Величина 
ничтожно мала, если отрезок времени между последовательными наблюдениями за частицей превышает 10-5 сек., что, конечно, всегда имеет место. Тогда можем записать:
. (3.24)
Для конечных промежутков времени 
и соответствующих перемещений 
, уравнение (3.24) можно переписать в виде:
.
Тогда
. (3.25)
Среднее значение квадрата смещения броуновской частицы за промежуток времени вдоль оси Х или другой любой оси, пропорционально этому промежутку времени. Формула (3.25) позволяет вычислить средние значения квадрата перемещений по всем частицам, участвующим в явлении. Но эта формула справедлива и для среднего значения квадрата многих последовательных перемещений одной единственной частицы за равные промежутки времени.
