Полное сопротивление (импеданс). Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи, обладающей емкостью, индуктивностью и активным сопротивлением R, переменного отока. Под действием внешнего напряжения (оно играет роль внешней э. д. с. ℇ)
(1)
Ток в цепи изменяется по закону
(2)
Где
(3)
РИС.1. ВЕКТОРНАЯ ДИАГРАММА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Векторная диаграмма здесь изображена для внешнего напряжения, представленного не как как 
, а как 
.
Задача сводиться к определению амплитуды силы тока и сдвига тока по фазе относительно U.
Полученное выражение для амплитуды силы тока 
можно формально толковать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе этого выражения величину, имеющую размерность сопротивления, обозначают буквой Z и называют полным сопротивлением или импедансом:
(4)
Видно, что при 
это сопротивление минимально и равно активному сопротивлению R. Величину, стоящую в круглых скобках формулы (4), обозначают X и называют реактивным сопротивлением:
(5)
При этом величину 
называют индуктивным сопротивлением, а величину 
- емкостным сопротивлением. Их обозначают соответственно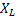 
и 
. Итак
(6)
Заметим, что индуктивное сопротивление растет с увеличением частоты 
а емкостное – уменьшается. Когда говорят, что в цели отсутствует емкость, то это надо понимать в смысле отсутствия емкость, то это надо понимать в смысле отсутствия емкостного сопротивления, которое равно и, следовательно, обращается в нуль, если С→∞ (при замене конденсатора закороченным участком).
И последнее. Хотя реактивное сопротивление измеряют в тех же единицах, что и активное, между ними существует принципиальное различие. Оно заключается в том, что только активное сопротивление определяет необратимые процессы в цепи, такие, как преобразование электромагнитной энергии в джоулеву теплоту.
Мощность, выделяемая в цепи переменного тока. Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:
(7)
Поскольку 
, преобразуем (7) к виду
Практически интерес имеет среднее за период колебания значению мощности. Учитывая, что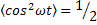 
и 
, получим:
. (8)
Это выражение можно привести к иному виду, если принять во внимание, что из векторной диаграммы следует 
. Поэтому
(9)
Такую же мощность развивает постоянный ток 
Величины
, 
(10)
Называют действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градуированы по действующим значениям тока и напряжения. Выражение средней мощности (8) через действующие значения напряжения и тока имеет вид
(11)
Где множитель 
принято называть коэффициентом мощности. Таки образом, выделяемая в цепи мощность зависит не только от напряжения и силы тока, но еще и от сдвига фаз между током и напряжением.
При 
значение 
, каковы бы ни были величины U и I. В этом случае энергия, передаваемая за четверть периода от генератора во внешнюю цепь, в точность равна энергии, передаваемой из внешней цепи в генератор в течении следующей четверти периода, и вся энергия бесполезно «колеблется» между генератором и внешней цепью.
Зависимость мощности от 
необходимо учитывать при проектировании линий электропередачи на переменном токе. Если питаемые нагрузки имеют большое реактивное сопротивление Х, то может быть заметно меньше единицы. В этих случаях для передачи потребителю нужной мощности (при данном напряжении генератора) необходимо увеличить ток I, а это приводит к возрастанию бесполезных потерь энергии в подводящих проводах. Поэтому всегда нужно стремиться распределять нагрузки, индуктивности и емкости так, чтобы был по возможности близок к единице. Для этого достаточно сделать реактивное сопротивление Х как можно меньше, т. е. обеспечить равенство индуктивного и емкостного сопротивлений (
.
