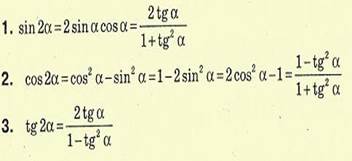Визначення логарифма
Означення: loga b читається: логарифм числа b по основі a.
Логарифм показує, в який ступінь треба піднести основу a, щоб отримати число b.
loga b = x рівносильно ax = b
Властивості логарифмів
Сума логарифмів дорівнює логарифму добутку
loga x + loga y = loga xy
Різниця логарифмів дорівнює логарифму дробу
loga x - loga y = loga x/y
Показник ступеню числа b можна винести за знак логарифму
loga xb = b loga x
Якщо основу a і число b піднести в однаковий ступень, значення логарифму не зміниться
logak bk = loga b
Для переходу до іншої основи логарифму формула:
Важливі випадки логарифмів
Десятковий логарифм - це логарифм по основі 10. Означається lg x. За визначенням log10 x = lg x. Десятковий логарифм часто використовується в технічних розрахунках.
lg 10 = 1, lg 10000 = 4, lg 0.001 = -3
Натуральний логарифм - це логарифм по основі e (де Неперово число e = 2,71828...). Означається ln x. За визначенням loge x = ln x. Натуральний логарифм широко використовується в математичних розрахунках, оскільки його похідна (ln x)/ = 1/x має більш простий вигляд, ніж для логарифмів з іншими основами.
ln e = 1, ln eb = b, в т.ч. b може бути від'ємним чи дробним, наприклад ln e-2 = -2
Основні формули тригонометрії