. (3)
Он определяет вектор напряженности 
электрического поля как функцию координат. Величина, стоящая в левой части уравнения (3), называется градиентом потенциала и обозначается символом 
или Ñ j.
. (4)
Градиент потенциала – это вектор, направленный в сторону наибыстрейшего возрастания скалярной величины 
. Вектор 
, по определению, направлен в сторону убывания потенциала, т.е. противоположно градиенту , поэтому в уравнении (3) стоит знак минус перед вектором .
Интегрирование уравнения (3) дает значение потенциала как функцию координат
. (5)
Если электрическое поле создается в проводящей среде, то оно описывается уравнением
. (6)
Это закон Ома в дифференциальной форме, где 
– плотность тока, – напряженность электрического поля, 
– удельная электропроводность среды. В случае изотропных сред их электрические свойства характеризуются единственным числом: 
– в диэлектрике и – в проводнике.
Плоский конденсатор. Поле плоского конденсатора, размеры пластин которого велики по сравнению с расстоянием между ними, однородно, т.е. напряженность в любой точке поля одинакова, а потенциал зависит только от расстояния до обкладок конденсатора. Примем потенциал одной из обкладок равным нулю, совместим с ней начало отсчета и направим ось х перпендикулярно ей в сторону другой обкладки (рис.1). Запишем для этого случая уравнение Лапласа
. (7)
Проинтегрируем его, в результате чего получим
. (8)
После второго интегрирования имеем
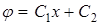. (9)
Обозначим расстояние между обкладками d, разность потенциалов между ними U. При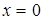 
потенциал 
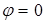, из формулы (9) следует С 2=0. При х = d потенциал 
, поэтому С 1 = 
. Подставляя С 1 в (9), получаем
, (10)
т.е. потенциал возрастает по линейному закону от нуля на левой обкладке до U на правой. Напряженность электрического поля направлена в сторону убывания потенциала, она постоянна по величине и направлению. В векторной форме ее можно записать так:
. (11)
Из формулы (10) видно, что плоскости x = const, параллельные обкладкам, представляют собой эквипотенциальные поверхности. Линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям, в том числе и поверхности электродов или обкладок конденсатора. Таковы результаты решения уравнения Лапласа.
Цилиндрический конденсатор. Если длина цилиндрического конденсатора велика по сравнению с радиусами внутренней и внешней обкладок r1, r2, то поле зависит только от расстояния r от оси конденсатора, и уравнение Лапласа в цилиндрической системе координат запишется так:
. (12)
После первого интегрирования уравнения (12) получается следующее:
. (13)
Второе интегрирование дает
. (14)
Полагая, что 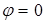при 
и при 
, определяем константы интегрирования
; 
.
Подставляя эти значения в уравнение (14), получаем
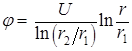, (15)
т.е. потенциал возрастает в направлении от внутренней обкладки к наружной (если наружная обкладка положительна). Напряженность поля при этом направлена радиально от наружной обкладки к внутренней
, (16)
где 
– единичный вектор радиального направления.
Из двух последних уравнений следует, что цилиндрические поверхности 
, в том числе и обкладки, являются поверхностями равного потенциала, а линии напряженности поля ортогональны им.
Если пространство между электродами рассмотренных конденсаторов сплошь заполнить электролитом и приложить к электродам разность потенциалов, то соотношения (10), (11), (15) и (16) для потенциала и поля остаются в силе. Линии напряженности электрического поля, в силу действия формулы (6), совпадают с линиями тока и перпендикулярны эквипотенциальным поверхностям, в том числе и поверхностям электродов.
В случае электродов сложной формы условие ортогональности силовых линий напряженности поверхности электродов в электрическом поле выполняется всегда. В электропроводной модели для выполнения этого условия необходимо, чтобы электропроводность электродов была гораздо больше электропроводности среды, заполняющей межэлектродное пространство.
Описание установки. Экспериментальная установка представляет собой плоскую горизонтальную кювету, в которую наливается жидкий электролит – прокипяченная водопроводная вода. Электропроводность ее вполне подходит для проведения подобных опытов. В воду помещены два неподвижных электрода А, В и один подвижный – зонд С.
Форму и размеры неподвижных электродов экспериментатор может менять в зависимости от поставленной задачи.
 |
Электрическая схема установки представлена на рис.2. К неподвижным электродам подведено переменное напряжение от понижающего трансформатора. Применение постоянного тока в данном случае нежелательно в связи с явлением поляризации электродов.
В качестве измерительного прибора используется цифровой электронный вольтметр В7-38. Его применение оправдано тем, что входное сопротивление вольтметра (500 кОм) значительно больше сопротивления того участка цепи, куда он включается, поэтому его включение практически не изменяет конфигурацию поля и не влияет на точность результатов измерения.
Одна из клемм вольтметра соединена с электродом В. Следовательно, вольтметр измеряет фактически разность потенциалов между электродами В и С. Но если потенциал электрода В принять за нуль, то показания вольтметра будут численно равны потенциалам точек электрического поля, в которые помещается подвижный зонд С.
Измерения. 1.Налейте в кювету воду, предназначенную для этой работы, в количестве 300-400 мл, чтобы ее слой составлял около 1 см.
2.С помощью установочных винтов отрегулируйте положение кюветы так, чтобы слой воды в ней был одинаковой толщины.
3.Закрепите на откидном столике лист бумаги формата А4.
4.Погрузите в воду и закрепите плоские электроды.
5.Соберите электрическую цепь по схеме (рис.2) и предложите преподавателю или лаборанту проверить правильность сборки.
6.Включите в сеть 220 В трансформатор и вольтметр, поставив при этом переключатель рода работы вольтметра на измерение переменного напряжения.
7.Откинув столик с бумагой на опорный кронштейн, прикоснитесь зондом в электроду. Опустите столик на острие зонда так, чтобы на бумаге остался след от прикосновения острия. Далее нанесите на бумагу еще 4-5 уколов, причем крайние из них следует совместить с границами электрода. В дальнейшем Вы сможете изобразить на бумаге форму и местоположение данного электрода. Точно так же нанесите на бумагу положение второго электрода. Запишите около каждого электрода показания вольтметра.
8.Перемещая зонд в пространстве между электродами, найдите точку поля, в которой вольтметр показывает 1,0 В, и перенесите ее положение на планшет. Найдите еще не менее пяти точек поля в различных местах кюветы с таким же потенциалом, каждый раз перенося их на планшет.
9.Подобным образом нанесите на лист бумаги точки с потенциалом 2,0; 3,0 В и т.д. Около каждой серии точек подписывайте соответствующий им потенциал (показания вольтметра).
 |
10.Замените плоские электроды теми, которые Вам предложит преподаватель из приведенных на рис.3, и проведите с ними те же измерения (пп. 7-9) на новом чистом планшете.
11.Закончив работу, выключите приборы и соберите воду из кюветы в подходящий сосуд с помощью груши.
Обработка результатов измерений. 1.На каждом из полученных планшетов проведите карандашом контуры электродов.
2.Экспериментальные точки (наколы) с одинаковым потенциалом соедините пунктирными линиями. Это будут эквипотенциальные линии электрического поля.
3.Постройте линии напряженности электрического поля, имея в виду, что они ортогональны линиям равного потенциала. Их принято проводить с такой густотой, чтобы соседние эквипотенциальные и силовые линии образовывали, пересекаясь, приблизительно квадраты.
4.Постройте график зависимости потенциала электрического поля вдоль одной из силовых линий от расстояния, выбрав за начало отсчета электрод с нулевым потенциалом.
5.Вычислите модуль вектора напряженности электрического поля вдоль одной из силовых линий в случае плоского конденсатора и вдоль двух удаленных друг от друга линий – в случае поля более сложной конфигурации. Постройте соответствующие графики для обоих случаев.
Контрольные вопросы
1.Каким уравнением описывается электростатическое поле в вакууме?
2.Почему электростатическое поле можно моделировать посредством поля тока? Всегда ли это можно сделать?
3.Решите уравнение Лапласа для электрического поля плоского и цилиндрического конденсатора. Что такое граничные условия?
4.Как из экспериментальной карты поля получить его характеристики: напряженность и потенциал.
5.Нарисуйте схему экспериментальной установки и расскажите о методике проведения измерений и обработки результатов.
6.Обоснуйте правомерность замены постоянного тока переменным в данной работе.
Список рекомендуемой литературы
1.Калашников С.Г. Электричество. М.: Наука, 1977. §8-13, 17-19.
2.Практикум по физике: Электричество и магнетизм /Под ред. Ф.А.Николаева. М.: Высшая школа, 1991. С.24-28.
3.Савельев И.В. Курс физики: Электричество и магнетизм. М.: Наука, 1998. Кн.2. §1.5 – 1.8; 1.14.
4.Сивухин Д.В. Общий курс физики: Электричество. М.: Наука, 1983. §3,18,19.
5.Матвеев А.Н. Электричество и магнетизм. М.: Высшая школа, 1983.
[1] Данной работе предшествовала другая – «Моделирование электростатического поля на электропроводной бумаге», которая была поставлена Г.Н.Хлебутиным.
