Французский ученый Луи де Бройль выдвинул в гипотезу, что все частицы должны обладать волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия Е и импульс р, а с другой — волновые характеристики — частота n и длина волны l. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:
E = hn, p = h/l. (3.6.1)
Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:
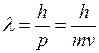(3.6.2)
Гипотеза де Бройля была подтверждена экспериментально. В 1927 г. американские физики К.Дэвиссон и Л.Джермер обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кристалла никеля,— дает отчетливую дифракционную картину.
Одним из основных признаков элементарных частиц является их неделимость. Например, заряд может быть передан от одного тела к другому только в количестве, кратном заряду электрона. Таким свойствам, как неделимость, волны не обладают.
Если целостность частиц (электронов, в частности) при таких процессах как преломление, отражение, – сохраняется, то можно утверждать, что при падении на поверхность раздела частица либо отражается, либо преломляется. Но в таком случае волновые свойства частиц могут быть истолкованы только статистически.
В этом случае поведение каждой отдельной частицы не может быть определено с достоверностью, а может быть лишь указана вероятность того или иного поведения частицы.
Рассмотрим упрощённую схему опыта по дифракции на одной щели шириной d.
Рис. 3.8.
Оценим неопределённости в координате и импульсе, появляющиеся после попадания микрочастицы в щель преграды. Пусть щель располагается перпендикулярно к направлению движения микрочастицы. До взаимодействия со щелью Δpx = 0, а координата х микрочастицы является полностью неопределённой. При прохождении частицей щели вследствие дифракции появляется неопределённость:
Δpx = p sin a (3.6.3)
Условие первого минимума при дифракции на одной щели.
d sina = l (3.6.4)
C учётом, что d = Δх имеем:
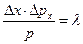(3.6.5)
Откуда воспользовавшись формулой де Бройля (3.6.2), получаем соотношение:
Δх·Δpx = h (3.6.6)
Полученное выражение является частным случаем соотношений неопределённостей Гейзенберга (1927 г.), и устанавливающих количественную связь между неопределённостями в определении координаты и соответствующей этой координате составляющей импульса (принцип неопределённости – нельзя одновременно точно определить значение координаты и импульса микрочастицы).
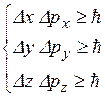
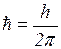(3.6.7)
Соотношение неопределённостей работает и для неопределённостей в энергии какой либо системы ΔЕ и времени Δt существования этой системы в состоянии с данной энергией Е:
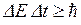(3.6.8)
Физический смысл соотношения (3.6.8) заключается в том, что из-за конечности времени жизни атомов в возбужденном состоянии энергия возбужденных состояний атомов не является точно определенной, а поэтому соответствующий энергетический уровень характеризуется конечной шириной. Из-за размытости возбужденных уровней энергия излучаемых фотонов характеризуется некоторым разбросом.
Физически разумная неопределённость Δp или Δx, во всяком случае, не должна превышать значения самого импульса p или координаты x, таким образом Δp £ p; Δx £ x.
Важно понять, что принцип неопределённости является сугубо физическим принципом и никак не связан с особенностями измерительных приборов. Из него вытекают очень важные следствия, характеризующие всю квантовую механику:
1. Микрочастицы не могут покоиться (например, электроны движутся вокруг ядра).
2. Для микрочастиц отсутствует понятие траектории (обычно избегают понятия скорости, ускорения, силы – нет точки её приложения).
Принцип неопределённостей играет роль фундамента квантовой механики, так как не только устанавливает физическое содержание и структуру её математического аппарата, но и правильно предсказывает результаты многих задач, связанных с движением микрочастиц. Является квантовым ограничением применимости классической механики к микрообъектам.
