7.1 Решить следующую задачу Коши для уравнения теплопроводности:
.
Ответ. 
.
7.2.. Используя решение задачи 7.1, показать, что решение задачи Коши
, 
можно представить в виде 
(формула Пуассона).
7.3 В теплоизолированный с боков стержень плотности r, площади поперечного сечения S в момент времени t=0 на отрезке [x-h, x+h] мгновенно вводится количество тепла, равное crS. Показать, что начальное распределение температур будет иметь вид 
, и 
.
В чём заключается физический смысл функции, найденной при решении задачи 7.2 (фундаментального решения уравнения теплопроводности)? 
. 7.4. Найти распределение температуры u(x, t) в бесконечном стержне, если начальное распределение температуры имеет вид 
.
Ответ. 
, где 
.
7.5. Распределение температур задано функцией 
– фундаментальным решением уравнения теплопроводности (смотри зад. 7.1). Построить график изменения температуры в зависимости от времени при фиксированном 
.
Указание. 
Максимум температуры достигается при 
и равен 
.
7.6. Доказать, что если функция 
в задаче Коши
,
нечётная, то 
.
7.7. Доказать, что если функция в задаче Коши
, 
чётная, то 
.
7.8. Используя метод отражения, решить уравнение
при начальном условии 
и краевом условии 
Изобразить кривую, выражающую зависимость температуры 
от 
для нескольких
Указание. Используя результат задачи 7.6, нужно положить
и использовать формулу Пуассона из задачи 7.2.
Ответ. 
.
7.9. Пусть конец 
полубесконечного стержня (
) теплоизолирован, т.е.
. Начальное распределение температуры: 
.
Определить распределение температуры в стержне в любой момент времени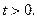 
Ответ. 
7.7. Задача Дирихле для круга. Найти функцию 
, (
– полярные координаты), удовлетворяющую уравнению 
внутри круга 
и принимающую заданные значения на его границе: 
. (См. Пискунов, Дифф. и интегр. исчисления, т.2, XXIX, §10).
Указание. Уравнение 
в полярных координатах имеет вид
или 
..\ММФ\Уравнение Лапласа.doc
Ответ. 
