Пример выполнения курсовой работы.
Титульный лист
Содержание.
Постановка задачи.
Исходная функциональная зависимость представлена в таблице парами значений xi и yi.
Найти параметры (С1 и С2) аппроксимирующей функции y = C1 + C2 x, пользуясь МНК. Поиск параметров осуществить, используя условия локального минимума критерия аппроксимации (т.е. решая систему нормальных уравнений). Оценить погрешность аппроксимации посредством критерия качества J и максимального по модулю отклонения аппроксимирующей функции от исходной.
Табличное представление исходных данных.
Таблица 1.
| i | |||||
 x x  
| 0,0 | 1,0 | 2,0 | 3,0 | 4,0 |
y 
| 0,0 | 1,0 | 8,0 | 27,0 | 64,0 |
5. Критерий аппроксимации (по пп. 2.1. пособия).
Согласно условию (2.5):
 J(C1, C2 ) =
J(C1, C2 ) =  min.
min.
Способ минимизации критерия аппроксимации.
В соответствии с требованием использования условий локального минимума (2.9) условия минимума J
 =0,
=0, 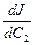 =0,
=0,
 =
=  = - 2 (
= - 2 ( ),
),
- 34 -
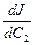 =
=  - 2 (
- 2 (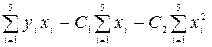 ),
),
т.е. нормальные уравнения имеют вид
- 2 ( ) =0,
) =0,
- 2( )=0
)=0
Или
C1 ·5 + C2  ,
,
C1  .
.




