А9. При каких значениях 
матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
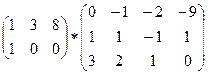С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б)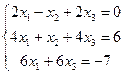 
|
в)  .
|
Вариант 26
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
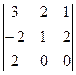А4. Найти алгеброические дополнения элементов 
и 
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу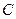 
, полученную путем преобразований матриц 
и 
:
.
; 
А8. Вычислить:
.
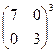А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
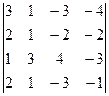В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б)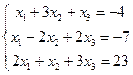 
|
в)  .
|
Вариант 27
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
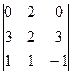А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 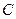, полученную путем преобразований матриц и :
.
;
А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б) 
|
в)  .
|
Вариант 28
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
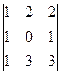А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 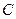, полученную путем преобразований матриц и :
.
;
А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
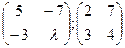
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б) 
|
в)  .
|
Вариант 29
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
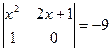А3. Вычислить определитель, пользуясь правилом треугольника:
.
А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
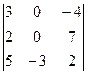А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 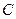, полученную путем преобразований матриц и :
.
;
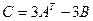А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а)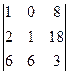 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б) 
|
в)  .
|
Вариант 30
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 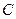, полученную путем преобразований матриц и :
.
;
А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
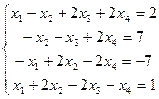С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б) 
|
в)  .
|
Решение типового варианта
А1. Вычислить определитель:
а) 
; б)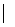 
.
Определитель второго порядка вычисляется по формуле (). Поэтому:
а) 
;
б)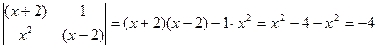 
.
А2. Решить уравнение:
,
Отсюда следует: 
, 
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
По формуле () получим:
.
А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
Выберем четвертый столбец т.к. в нем содержится больше всего нулей и будем вычислять используя понятие алгебраическое дополнение.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
а) Составим главный определитель системы из коэффициентов перед неизвестными 
Составим вспомогательный определитель 
из главного путем замены первого столбца на столбец свободных членов 
Составим вспомогательный определитель 
из главного путем замены второго столбца на столбец свободных членов 
По формулам Крамера получим: 
б) Составим главный определитель системы из коэффициентов перед неизвестными 
Данный определитель вычисляется любым известным нам способом.
