А8. Вычислить:
.
А9. При каких значениях 
матрица не имеет обратную?
А10. Решить матричное уравнение:
.
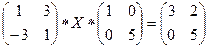А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
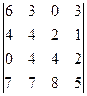В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
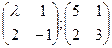
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б) 
|
в)  .
|
Вариант 7
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
А4. Найти алгеброические дополнения элементов 
и 
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу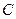 
, полученную путем преобразований матриц 
и 
:
.
; 
А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
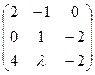
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
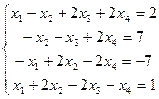
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,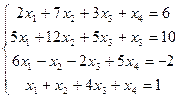
| б)  ,
|
в)  .
|
Вариант 8
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 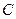, полученную путем преобразований матриц и :
.
;
А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
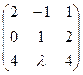
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а)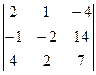 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
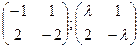
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,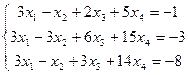
| б) 
|
в)  .
|
Вариант 9
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
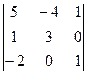А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 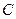, полученную путем преобразований матриц и :
.
;
А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
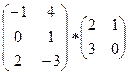С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б) 
|
в)  .
|
Вариант 10
А1. Вычислить определитель:
а)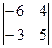 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б)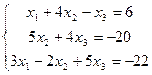 
|
А7. Найти матрицу 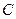, полученную путем преобразований матриц и :
.
;
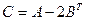А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
| а) | б)  ,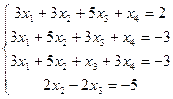
|
в)  .
|
Вариант 11
А1. Вычислить определитель:
а)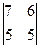 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 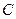, полученную путем преобразований матриц и :
.
;
А8. Вычислить:
.
А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
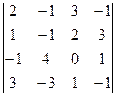В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 
| б)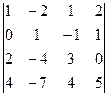 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
В5. Найти обратную матрицу:
.
В6. Найти ранг матрицы методом Гаусса:
.
В7. Решить методом Гаусса систему уравнений:
.
С1. Умножить матрицы:
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
С3. Решить методом Гаусса системы уравнений:
а)  ,
| б) 
|
в)  .
|
Вариант 12
А1. Вычислить определитель:
а) 
б) 
.
А2. Решить уравнение:
.
А3. Вычислить определитель, пользуясь правилом треугольника:
.
А4. Найти алгеброические дополнения элементов и определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 
| б) 
|
А7. Найти матрицу 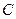, полученную путем преобразований матриц и :
.
;
А8. Вычислить:
.
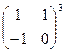А9. При каких значениях матрица не имеет обратную?
А10. Решить матричное уравнение:
.
А11. При каких значениях матрица имеет ранг, равный 1?
В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а)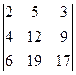 
| б) 
|
В3. Умножить матрицы:
.
В4. При каких значениях матрицы перестановочны?
