2.1. Понятие о марковском процессе
Рассмотрим сравнительно благоприятный случай стохастической неопределенности, когда неопределенные факторы, входящие в задачу, представляют собой случайные величины, вероятностные характеристики которых либо известны, либо могут быть получены из опыта. Главным образом, мы будем заниматься прямыми задачами исследования операций, т.е. построением математических моделей некоторых случайных явлений. В стохастических задачах исследования операций часто затруднительно даже построение математической модели, не говоря уже об оптимизации. Однако в некоторых особых случаях такую математическую модель удается построить. Это – когда исследуемая операция представляет собой так называемый марковский случайный процесс.
Пусть имеется некоторая физическая система 
, которая с течением времени меняет свое состояние (переходит из одного состояния в другое), причем заранее неизвестным, случайным образом. Пусть в настоящий момент 
(рис.) система находится в определенном состоянии 
. Мы наблюдаем процесс со стороны и в момент знаем состояние системы и всю предысторию процесса, все, что было при 
. Нас, естественно, интересует будущее 
. Можем ли мы его предсказать? В точности – нет, наш процесс случайный, значит – непредсказуемый. Но какие-то вероятностные характеристики процесса в будущем мы можем найти. Например, вероятность того, что через некоторое время 
система окажется в состоянии 
или сохранит состояние . Если процесс марковский, то предсказывать можно, только учитывая настоящее состояние системы и забыв о его предыстории (поведение системы при ). Само состояние , разумеется, зависит от прошлого, но как только оно достигнуто, о прошлом можно забыть. Иначе формулируя, в марковском процессе будущее зависит от прошлого только через настоящее.
Итак, дадим определение марковского случайного процесса. Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент и не зависят от того, когда и как система пришла в это состояние.
На практике марковские процессы в чистом виде обычно не встречаются, но нередко приходится иметь дело с процессами, для которых влиянием предыстории можно пренебречь. При изучении таких процессов можно с успехом применять марковские модели.
В исследовании операций большое значение имеют так называемые марковские случайные процессы с дискретными состояниями и непрерывным временем. Процесс называется процессом с дискретными состояниями, если его возможные состояния 
можно заранее перенумеровать, и переход системы из состояния в состояние происходит скачком, практически мгновенно. Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а случайны, т.е. переход может осуществиться в любой момент.
Пример такого процесса: техническое устройство состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя (отказать), после чего мгновенно начинается ремонт узла, тоже продолжающийся заранее неизвестное, случайное время. Возможные состояния можно перечислить:
оба узла исправны,
первый узел ремонтируется, второй исправен,
второй узел ремонтируется, первый исправен,
оба узла ремонтируются.
Переходы системы из состояния в состояние происходят практически мгновенно, в случайные моменты выхода из строя того или другого узла или окончания ремонта.
При анализе случайных процессов с дискретными состояниями обычно используют так называемый граф состояний. Построим граф состояний для рассмотренного примера (рис.).
Если процесс, протекающий в системе с дискретными состояниями и непрерывным временем, является марковским, то для его описания можно построить довольно простую математическую модель. Но перед этим познакомимся с важным понятием теории вероятностей – понятием «потока событий».
2.2. Потоки событий
Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Например: поток вызовов на телефонной станции; поток отказов (сбоев) ЭВМ; поток железнодорожных составов, поступающих на сортировочную станцию.
Важной характеристикой потока событий является его интенсивность 
- среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной (
), так и переменной, зависящей от времени 
. Например, поток автомашин, движущихся по улице, днем интенсивнее, чем ночью, в часы пик – интенсивнее, чем в другие часы.
Поток событий называется регулярным, если события следуют одно за другим через определенные, равные промежутки времени. На практике чаще встречаются потоки не регулярные, со случайными интервалами.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока должна быть постоянной. На практике часто встречаются потоки событий, которые (по крайней мере на ограниченном участке времени) могут считаться стационарными. Например, поток вызовов, поступающих на АТС между 13 и 14 часами, практически стационарен; но тот же поток в течение суток уже не стационарен.
Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени 
и 
число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга, вызванные каждое своими собственными причинами. Например, поток пассажиров входящих в метро, практически не имеет последействия. А вот поток пассажиров выходящих из метро, уже имеет последействие.
Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по несколько сразу. Например, поток клиентов, направляющихся в парикмахерскую или к зубному врачу, обычно ординарен, чего нельзя сказать о потоке клиентов, направляющихся в загс для регистрации браков. Если поток событий ординарен, то вероятностью попадания на малый участок времени 
двух или более событий можно пренебречь.
Поток событий называется простейшим, если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последействия.
В расчетах, связанных с потоками событий, очень удобно пользоваться понятием «элемента вероятности». Рассмотрим на оси 
простейший поток с интенсивностью и произвольно расположенный элементарный (очень маленький) участок времени . Элементом вероятности называется вероятность попадания на этот участок хотя бы одного события потока. Для простейшего потока элемент вероятности равен интенсивности потока, умноженной на длину элементарного участка.
(6)
Элемент вероятности, в силу отсутствия последействия, совершенно не зависит от того, сколько событий и когда появлялись ранее.
Поток событий называется рекуррентным, если он стационарен, ординарен, а интервалы времени между событиями 
представляют собой независимые случайные величины с одинаковым произвольным распределением. Пример: технический элемент (радиолампа) работает непрерывно до своего отказа (выхода из строя); отказавший элемент мгновенно заменяется новым. Если отдельные экземпляры элемента выходят из строя независимо друг от друга, то поток отказов будет рекуррентным.
2.3. Уравнения Колмогорова для вероятностей состояний.
Финальные вероятности состояний.
Рассматривая марковские процессы с дискретным состоянием и непрерывным временем удобно представлять, что все переходы системы из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, поток отказов, поток восстановлений и т.д.). Если все потоки событий, переводящие систему из состояния в состояние – простейшие, то процесс протекающий в системе, будет марковким (это достаточное, но не необходимое условие). Это и естественно, так как простейший поток не обладает последействием: в нем «будущее» не зависит от «прошлого».
Если система находится в каком-то состоянии 
, из которого есть непосредственный переход в другое состояние 
, то это можно представить так, как будто на систему, пока она находится в состоянии , действует простейший поток событий. Как только появится первое событие этого потока, происходит «перескок» системы из в .
Для наглядности проставим на графе состояний интенсивности потоков событий. Обозначим через 
интенсивность потока событий переводящего систему из состояния в . Граф состояний с проставленными интенсивностями называется размеченным.
Построим такой граф. Интенсивность потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии . Какой поток событий переводит ее в состояние ? Очевидно, поток отказов первого узла. Его интенсивность 
равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из в ? Очевидно, поток «окончания ремонтов» первого узла. Его интенсивность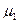 
равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа (рис).
Пусть рассматривается система , имеющая 
возможных состояний 
. Назовем вероятностью 
го состояния вероятность 
того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма всех вероятностей состояний равна 1: 
.
Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний как функции времени. Для этого составляются и решаются так называемые уравнения Колмогорова – особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний.
Рассмотрим на конкретном примере, как эти уравнения составляются.
….
Это система 4 линейных дифференциальных уравнений с 4-мя неизвестными функциями 
. Одно из них любое можно отбросить, заменив его условием нормировки 
.
Сформулируем теперь общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности какого-то ( го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния умноженная на вероятность данного ( го) состояния.
Чтобы решить уравнения Колмогорова и найти вероятности состояний необходимо, прежде всего, задать начальные условия.
Полученную таким образом систему дифференциальных уравнений можно решить с использованием преобразования Лапласа.
…
Однако исследователя часто интересует вопрос, что будет происходить с вероятностями состояний при 
. Будут ли вероятности состояний стремится к каким-то пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний. В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то финальные вероятности существуют.
Предположим, что это условие выполнено, и финальные вероятности существуют:
При в системе устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Финальную вероятность состояния можно истолковать как среднее относительное время пребывания системы в этом состоянии. Как же вычислить финальные вероятности?
Если вероятности 
постоянны, то их производные равны нулю. Значит, все левые части уравнений Колмогорова будут равны нулю. И мы имеем уже систему не дифференциальных, а линейных алгебраических уравнений.
