Решить систему уравнений методом Гаусса

Вычислить определитель.

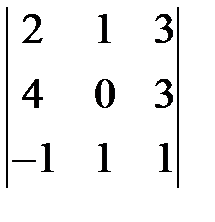
Решение:

1-й способ: по определению («правило Саррюса» или «метод треугольников») имеем:

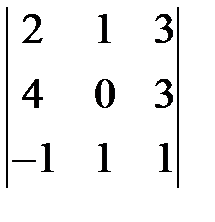= 2*0*1 – 2*3*1 – 4*1*1 + 4*3*1 + (-1)*1*3 - (-1)*3*0 = -1

 

2-й способ: разложением по второй строке получим:

=

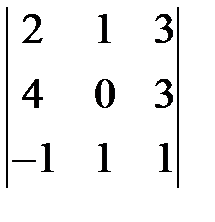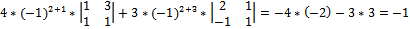
Ответ: -1

Найти матрицу Х из матричного уравнения (решать, используя обратную матрицу).

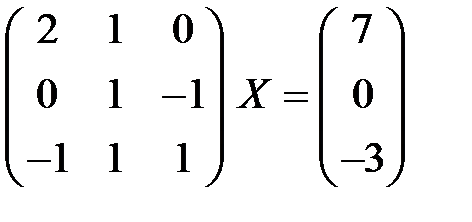
Решение:

Матричное уравнение вида AX = B где A - квадратная невырожденная матрица порядка n,

а B - матрица размера n х q, решается умножением обеих частей

слева на A^- - обратную матрицу к матрице A (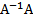 = E - единичная матрица):

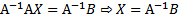
В нашей задаче А=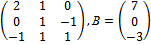

Проверим, что матрица A невырождена, т.е. ее определитель det A ≠ 0.

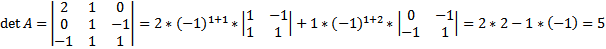
Обратную матрицу находим по формуле ,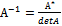

где 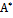-присоединенная матрица, элементами которой являются алгебраические дополнения соответствующих элементов транспонированной матрицы .

 

=

 

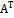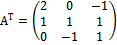
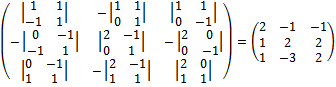
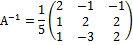
Матрицу Х ищем по формуле: X = A^-1·B

*

 

 

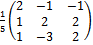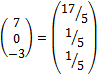
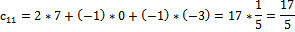
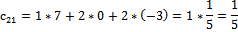
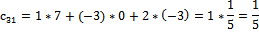
Ответ: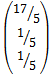

Решить систему уравнений методом Гаусса.

 

 

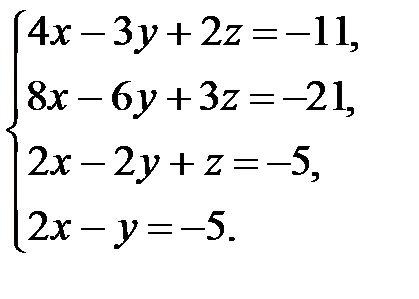
Перепишем систему уравнений в матричном виде и решим методом Гаусса

 

 

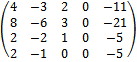
1-ую строку делим на 4

 

от 2; 3; 4 строк отнимаем 1 строку, умноженную соответственно на 8; 2; 2

 

 

поменяем 2-ую строку и 3-ую строку местами

 

2-ую строку делим на -0.5

 

от 1; 4 строк отнимаем 2 строку, умноженную соответственно на -0.75; 0.5

 

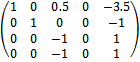
3-ую строку делим на -1

 

 

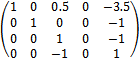
от 1; 4 строк отнимаем 3 строку, умноженную соответственно на 0.5; -1

 

Ответ: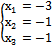

4.3 Найти площадь и длины диагоналей параллелограмма, построенного на векторах .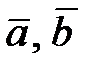

.

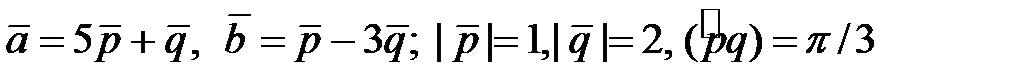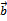
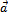
Решение: Известно, что векторы, совпадающие с диагоналями, выражаются формулами

=

=

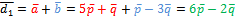
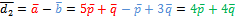
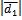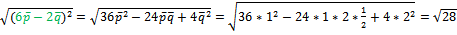
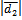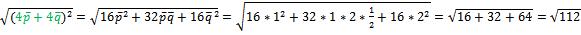
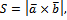(2)

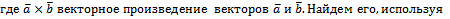
алгебраические свойства векторного произведения:

( (

( )

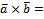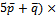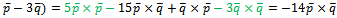
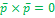
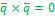Тогда, по формуле (2), учитывая свойство векторного произведения

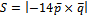=14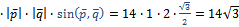

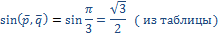
Ответ:

5.3Даны вершины треугольника А, В, С. Найти косинус угла ВАС, проекцию стороны АВ на сторону АС и площадь треугольника АВС.

A (3;3;–1); B (5;5;–2); C (4;1; 1).

1) 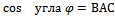найдем по формуле

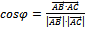, где

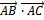- скалярное произведение векторов 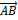и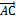

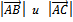-длины этих векторов

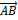= {5-3;5-3;-2-(-1)}={2;2;-1}

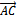= {4-3;1-3;1-(-1)}={1,-2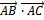,2}

=2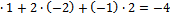

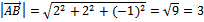
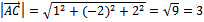
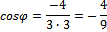
2) Проекцию 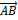на 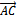находим по формуле

=

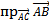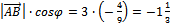
3)

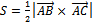
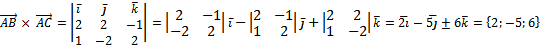
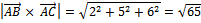
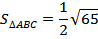
Ответ: ;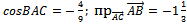

6.3 Вычислить объем тетраэдра с вершинами в точках A, B, C, D.

A (2;–1;2), B (1;2;–1), C (3;2;1), D (–4;2;5).

Решение. Найдем координаты векторов: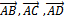

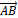= {1-2,2-(-1),-1-2}={-1,3,-3}

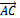= {3-2, 2-(-1), 1-2}={1,3,-1}

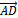= {-4-2,2-(-1),5-2}={-6,3,3}

Четыре точки A, B, C, D лежат в одной плоскости в том и только том случае, когда векторы 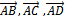компланарны, что равносильно равенству нулю их смешанного произведения 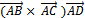. Найдем смешанное произведение по известной формуле

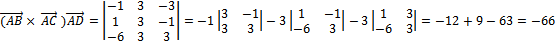
Значит A,B,C,D- точки, не лежащие в одной плоскости (являются вершинами тетраэдра ABCD).

Известно, что модуль смешанного произведения некомпланарных векторов 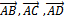равен объему параллелепипеда, построенного на этих векторах, а искомый объем тетраэдра составляет шестую часть объема этого параллелепипеда. Таким образом,

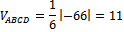
Ответ: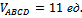

7.3. Даны вершины треугольника А (4;5), В (8,13), С (14;7). Найти координаты центра описанной около треугольника окружности.

Пусть О(x,y) центр описанной окружности – точка пересечения серединных перпендикуляров в треугольнике АВС.

1)Найдем уравнения сторон:

АВ: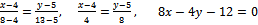

BC: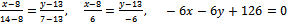

СА: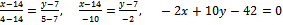

 

2) Найдем координаты середин сторон АВ, ВС,СА, обозначим их N,M,T соответственно

N: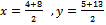

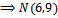
M: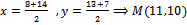

T: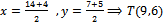

3)Найдем уравнения серединных перпендикуляров:

NO: (уравнение прямой, проходящей через точку 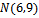перпендикулярно АВ )

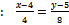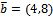направляющий вектор прямой АВ. Так как АВ 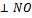, то координаты вектора 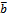являются координатами нормального вектора 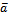прямой NO

уравнение прямой, проходящей через точку 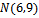и имеющей нормальный вектор 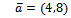записывается в виде

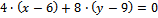4x+8y-96=0

MO: (уравнение прямой, проходящей через точку 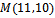перпендикулярно В )

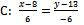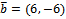направляющий вектор прямой ВС. Так как ВС 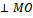, то координаты вектора 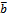являются координатами нормального вектора 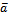прямой MO

уравнение прямой, проходящей через точку 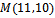и имеющей нормальный вектор 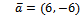записывается в виде

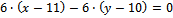6x-6y-6=0

TO: (уравнение прямой, проходящей через точку 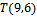перпендикулярно CА )

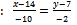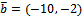направляющий вектор прямой CА. Так как CА 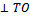, то координаты вектора 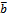являются координатами нормального вектора 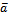прямой TO

уравнение прямой, проходящей через точку 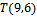и имеющей нормальный вектор 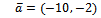записывается в виде

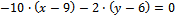-10x-2y+102=0

 

4) Найдем О(x,y) как точку пересечения MO,NO

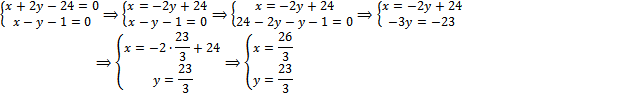
Подставим координаты найденной точки в уравнение прямой ТО

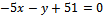
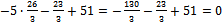, верно, следовательно

MO,NO и ТО пересекаются в точке О(8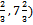

Сделаем проверку: так как О –центр описанной окружности, АО=ОВ=ОС

=

=

=

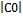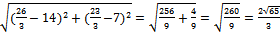
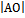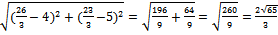
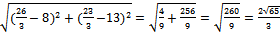
Ответ: О(8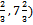

 

8.3. Найти уравнение плоскости, проходящей через точки 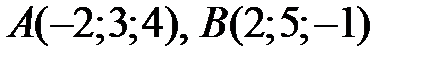и параллельной оси ОУ.

Решение:

Обозначим точку А за 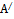, B за .

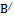Уравнение плоскости, проходящей через точку и имеющей нормальный вектор 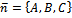, выглядит следующим образом:

А 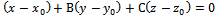(1)

Если плоскость параллельна ОY, то 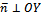и В=0, учитывая это, возьмем в качестве 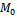точку 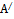, тогда, согласно (1) получим:

А(х-(-2))+0(y-3)+C(z-4)=0 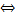Ax+2A+Cz-4C=0 (2)

Для определения А и С используем то, что точка 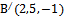принадлежит этой плоскости

2A+2A-C-4C=0

4A-5C=0

A= C, возьмем А=5 (выбираем значение сами, какое удобно)), тогда С=4

из(2) получим 5x+10+ 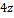-16=0 5x+4z-6=0

2-й способ:

Так как, согласно условию, искомая плоскость параллельна каждому из векторов

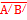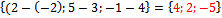= и 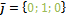(орт оси ОY), то по свойству векторного произведения, вектор 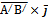является нормальным вектором плоскости. Найдем его координаты.

=

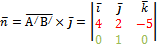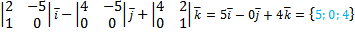
5(x+2) +0 (y-3) +4(z-4)=0 из (1) получим 5x+10+4z-16=0 5x+4z-6=0

(-2,3,4) –координаты точки А

Ответ: 5x+4z-6=0

9.3. Найти проекцию точки Р (–2;11;7) на плоскость .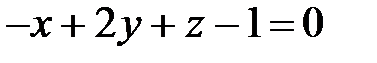

Искомая точка 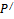лежит на пересечении прямой и плоскости, причем прямая проходит через точку Р перпендикулярно данной плоскости. Найдем координаты как решение системы уравнений данной плоскости и перпендикуляра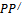

Вид канонических уравнений прямой, перпендикулярной плоскости и проходящей через точку Р (–2;11;7):

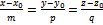, где 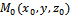- данная точка, т.е в нашей задаче P), а 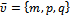направляющий вектор прямой, за который можно принять нормальный вектор плоскости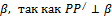

В нашем случае,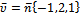

Таким образом, уравнения 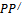имеют вид:

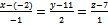
Перейдем от канонических уравнений к параметрическим:

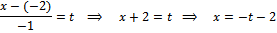
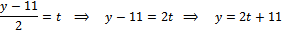
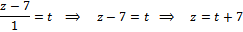
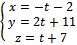(1)

 

Присоединим к данным уравнениям уравнение плоскости 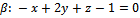(2)

И решим систему:

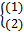
Для этого подставим x,y,z из (1) в (2)

( (

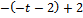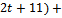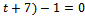
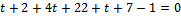
6t=-30

t=-5

подставляя t=-5 в (1), получим:

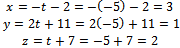
Найденная тройка чисел (3,1,2) удовлетворяет уравнениям прямой 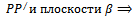определяет их точку пересечения.

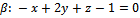-3+2+2-1=0

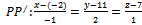
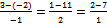
Ответ: 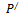(3,1,2)

 

10.3 Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.

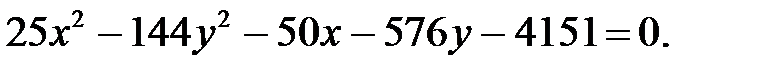
Преобразуем данное уравнение, выделяя в левой части полные квадраты

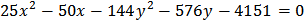
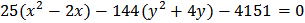
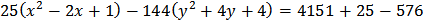
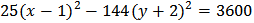
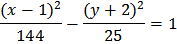
Если перенести начало координат в точку O' (х₀, у₀) и применить формулы преобразования координат при параллельном переносе 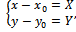где (x,y)- старые (данные) координаты (в системе Оxy), (XY) – её новые координаты (в системе O'XY), (х₀, у₀) - координаты нового начала O' в старой системе (Oхy), то уравнение

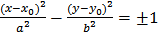
преобразуется к виду

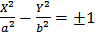
- каноническое уравнение гиперболы с центром O' и полуосями а и b

В нашем случае O' (1, -2) - центр гиперболы, ее уравнение (в новых координатах)

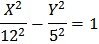
а= 12 - действительная полуось, b = 5 - мнимая полуось.

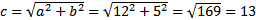полуфокусное расстояние

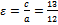эксцентриситет: отношение фокусного расстояния к длине действительной оси

Асимптоты гиперболы – прямые, заданные уравнениями Y= 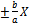, т.е. в нашем случае Y== 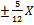, или в старой системе координат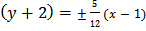

Директрисы - прямые, параллельные мнимой оси, удаленные от нее на расстояние ; для данной гиперболы их уравнения X= 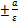, т.е. X=12* 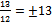, или, в старой системе, х-1=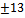

Для построения гиперболы строим «характеристический прямоугольник», диагоналями которого являются асимптоты, а стороны, параллельные осям, имеют длины 2а и 2b соответственно

 

 

Ответ: гипербола с центром O' (1, -2), действительной полуосью а= 12, мнимой b = 5

 

эксцентриситет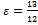

уравнения асимптот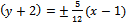

директрис х-1=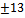

 

 

Литература:

1.Письменный Д.Т. Конспект лекций по высшей математике. 1 часть.

2.Лунгу К.Н. и др. Сборник задач по высшей математике. Линейная алгебра. Аналитическая геометрия. Основы математического анализа.

3.Данко П.Е. и др. Высшая математика в упражнениях и задачах. Часть 1.