Цель работы: овладеть навыками решения задачи поиска экстремума целевой функции методом половинного деления.
Метод половинного деления - это метод, согласно которому исходная длинна интервала поиска экстремума [A,B] на каждой итерации уменьшается почти вдвое, что обеспечивает эффективный поиск хопт.
Алгоритм метода включает следующие этапы:
· Определяет координаты точек х1 и х2, лежащих вблизи середины исходного интервала[A,B]
Для этого исходный интервал исследования делят пополам и от него в разные стороны откладывают отрезок Δх/2. Полученные точки ибудут соответствовать искомым х1 и х2. Значения Δх определяет наименьшую величину изменения аргумента. Процесс поиска оптимума представлен на рис 1.
Искомые значения х1 и х2:
Х1=А+(В-А)/2- Δх/2=А+(В-А- Δх)/2
Х2= А+(В-А)/2- Δх/2=А+(В-А+Δх)/2
· Определяют значения целевой функции у1 и у2 для двух точек х1 и х2:
Y1=f(x1) и Y2=f(x2)
· Ищут новый исходный интервал поиска, в котором находится искомый оптимум хопт. Для этого используют свойства унимодальной функции:
1. Если у2≥у1, то А=х1 – отбрасывается интервал [A,x1];
2. Если у2≤у1, то B=х1 – отбрасывается интервал [x2,B];
3. При этом,если у2>у1, то уmax=y1, ищется максимум функции у.
· Проверяют условия окончания процесса поиска оптимума:
· Если (В-А)< Δх, то процесс поиска заканчивается.
1.Проверяют число выполненных итераций i. Если число выполненных итераций I>N (максимальное допустимое), то процесс заканчивается, в противном случае переходят к началу алгоритма;
2. Если в методе прямого перебора эффективность поиска оптимума прямо пропорциональная числу расчетов, то по методу дихотомии она возрастает с ростом итераций экспоненциально. Отношения начального интервала поиска (В –А) к интервалу поиска (В-А)N после итераций приблизительно равна 2N/2, то есть
В-А/(В-А)N=2N/2
Если для метода прямого перебора требуется 1000 вычислений, то для метода дихотомии только 20
Программа
|
|
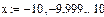
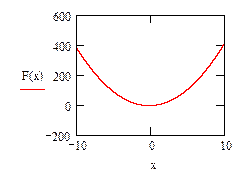
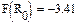
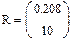
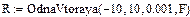
Функция и график 1 функция
|
|
|
|
