Уравнение (7) – одно из двух фундаментальных уравнений электростатики. Поле, обладающее свойством (7), называется потенциальным, т.е. любое электростатическое поле является консервативным или потенциальным.
Другим фундаментальным соотношением является теорема Гаусса (в интегральной форме), утверждающая, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную 
, т.е.
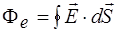
, (8)
где кружок у интеграла означает, что интегрирование проводится по замкнутой поверхности.
Теорема Гаусса в ряде случаев позволяет весьма простым путем рассчитывать напряженность электрического поля, созданного, например, одной заряженной плоскостью, двумя параллельными плоскостями, цилиндром, сферой, шаром и т.д.
Из вышесказанного следует, что электрическое поле можно описать либо с помощью векторной величины (вектора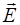 
), либо с помощью скалярной величины (потенциала 
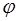). Так как эти величины являются характеристиками электрического поля, то между ними должна существовать определенная связь.
Связь между напряженностью электростатического поля и потенциалом можно выразить с помощью понятия градиента потенциала.
Градиент (потенциала) – вектор, показывающий направление наибольшего роста скалярной функции 
:
, (9)
где 
, 
– координатные орты.
Величина этого вектора равна изменению потенциала 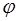при перемещении на единицу длины в направлении быстрейшего изменения.
Длина градиента (потенциала) равна
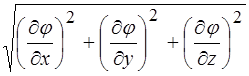. (10)
Из механики известно, что консервативная сила равна градиенту потенциальной энергии частицы, взятому с обратным знаком, т.е.
, (11)
где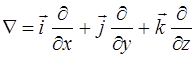 
– символический вектор, называемый оператором Гамильтона или оператором набла.
Для электростатического поля имеем:
.
Тогда соотношение (11) принимает вид
,
или 
, (12)
т.е. напряженность электрического поля равна градиенту потенциала с обратным знаком.
Знак минус в (12) показывает, что вектор направлен противоположно вектору градиента потенциала , и силовые линии электрического поля являются линиями, вдоль которых потенциал изменяется наиболее быстро.
Очевидно, что проекция вектора 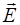на произвольное направление l равна со знаком минус частной производной потенциала по данному направлению:
. (13)
В случае однородного электрического поля (поля плоского конденсатора), в любой точке которого вектор напряженности 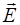постоянен как по величине, так и по направлению, имеем простое соотношение:
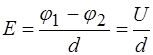, (14)
где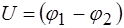 
– разность потенциалов или напряжение между пластинами конденсатора (или между двумя эквипотенциальными поверхностями);
– расстояние между пластинами конденсатора (или между двумя эквипотенциальными поверхностями).
Поверхность, все точки которой имеют одинаковый потенциал, называется поверхностью равного потенциала или эквипотенциальной поверхностью, для которой
. (15)
Из вышеизложенного следует, что электрическое поле можно изображать графически как с помощью силовых линий, так и пользуясь эквипотенциальными поверхностями.
Перенос заряда вдоль эквипотенциальной поверхности не требует работы (разность потенциалов двух любых точек этой поверхности равна нулю). Это означает, что сила, действующая на переносимый заряд, перпендикулярна к перемещению.
Следовательно, вектор 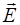всегда направлен по нормали к эквипотенциальной поверхности, т.е. линии напряженности в каждой точке ортогональны к эквипотенциальной поверхности.
Итак, можно сделать важный вывод о том, что электрическое поле полностью можно описать векторной величиной – напряженностью 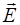. Но во многих случаях оказывается, что для вычисления напряженности 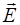электрического поля удобнее сначала определить потенциал φ и затем по формуле (12) вычислить напряженность 
. (В ряде задач с хорошей симметрией нахождение напряженности 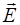непосредственно или с помощью теоремы Гаусса (8) оказывается значительно проще.)
Для исследования распределения потенциала в электростатическом поле системы заряженных проводников можно пользоваться методом электрического зонда. Зонд представляет собой тонкий кончик проволочки, выступающий из диэлектрической трубочки. Зонд, соединенный с электрометром, значительно меняет потенциал той точки поля, в которую он вносится. Это обусловлено возникновением индукционных зарядов, появляющихся на зонде и шарике электрометра. Хотя существует ряд способов удаления индукционных зарядов с зонда, но проведение эксперимента с электрометром весьма затруднительно.
Одним из способов изучения электростатического поля является метод математического моделирования полей.
Моделирование находит широкое применение как при научных исследованиях, так и при решении большого числа практических задач в различных областях техники [1].
При физическом моделировании некоторый объект (натура) и модель имеют одинаковую физическую природу, характер самого процесса сохраняется, но геометрические параметры модели отличаются от реального объекта.
При математическом моделировании закономерности различных по природе физических процессов описываются одинаковыми дифференциальными уравнениями и граничными условиями. Метод математического моделирования, сводящий исследование явлений различной физической природы к математическим задачам, нашел широкое применение в связи с развитием вычислительной техники.
В данной лабораторной работе моделью электростатического поля в диэлектрике может служить электрическое поле стационарного тока в слабопроводящей среде (при одинаковой геометрии электродов).
Подобие таких полей можно обосновать путем сопоставления их свойств.
Как указывалось выше, для электростатического поля теорема о циркуляции вектора напряженности электростатического поля имеет вид (7):
.
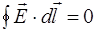При отсутствии источников сторонних сил поле в однородной проводящей среде описывается уравнением:
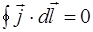, (16)
где – плотность тока, равная, согласно закону Ома в дифференциальной форме,
. (17)
Учитывая, что удельная электроводность данной проводящей среды
,
уравнение (16) можно представить в виде:
или
.
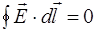Итак, форма уравнений не меняется от замены непроводящей среды (7) на слабопроводящую (16).
Также можно показать, что имеется подобие и между граничными условиями.
Действительно, на границе раздела диэлектриков нормальные и тангенциальные составляющие вектора напряженности электростатического поля подчиняются условиям [2,3]:
, 
, (18)
где 
– диэлектрические проницаемости первой и второй сред.
В случае слабопроводящей среды тангенциальные составляющие вектора напряженности потенциального поля тока непрерывны, а граничные условия для нормальных составляющих вытекают из уравнения непрерывности, т.е.
или 
. (19)
Таким образом, из подобия граничных условий следует, что для изучения электростатического поля можно использовать поле тока в слабопроводящей среде; силовым линиям электрического поля будут соответствовать линии тока, а эквипотенциальным поверхностям – поверхности равных напряжений.
