ИЗМЕРЕНИЯ:
Подведите маркер мыши к движку регулятора вблизи картинки спектра, нажмите левую кнопку мыши и, удерживая ее в нажатом состоянии, двигайте движок, установив числовое значение длины волны l1, взятое из таблицы 1 для вашей бригады.
Аналогичным образом, зацепив мышью движок регулятора расстояния между щелями, установите минимальное значение d = 1 мм. Измерьте, используя шкалу на экране, расстояние XMAX между нулевым и первым максимумами и запишите в таблицу 2. Увеличивая d каждый раз на 0.3 мм, измерьте еще 9 значений расстояния XMAX.
Устанавливая новые числовые значения длины волны l, из таблицы 1 для вашей бригады, повторите измерения по п.2, записывая результаты в таблицы 3,4,5.
ТАБЛИЦА 1. Примерные значения длины волны (не перерисовывать)
| Бригада | ||||||||
| l1 | ||||||||
| l2 | ||||||||
| l3 | ||||||||
| l4 |
ТАБЛИЦЫ 2-5. Результаты измерений при l = ____ нм
| d[мм] | ||||||||||
| XMAX[мм] | ||||||||||
| 1/XMAX [мм-1] |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
Рассчитайте и внесите в таблицы значения обратного расстояния между щелями.
Постройте на одном рисунке графики экспериментальных зависимостей смещения первого максимума XMAX от обратного расстояния между щелями (указав на них длину волны l).
Для каждой линии определите по графику экспериментальное значение произведения lL, используя формулу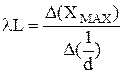 
.
Рассчитайте среднее значение экспериментально полученного произведения lL и абсолютную ошибку измерений данного произведения.
Запишите ответ и проанализируйте ответы и графики.
Вопросы и задания для самоконтроля
1. Что такое волна?
2. Что такое гармоническая волна?
3. Что такое длина волны?
4. Напишите математическое условие того, что функция f(x,t) описывает волну.
5. Что определяет форму волны и направление ее распространения?
6. Напишите математическую функцию, определяющую одномерную гармоническую волну, распространяющуюся в положительном направлении оси ОХ.
7. Что такое когерентность?
8. Дайте определение когерентных волн.
9. Дайте определение явления интерференции.
10. Дайте определение явления дифракции.
11. Что такое волновая поверхность?
12. Сформулируйте принцип Гюйгенса.
13. Дайте определение зон Френеля.
14. Напишите формулу для напряженности электрического поля dE электромагнитной волны (ЭМВ), излучаемой элементарным участком площадью dS волновой поверхности в точке наблюдения, расположенной на расстоянии r от этого участка. Поясните рисунком.
15. Что такое разность хода двух гармонических волн, излучаемых двумя источниками.
16. При какой разности хода двух волн при их сложении наблюдается максимум?
17. При какой разности хода двух волн при их сложении наблюдается минимум?
ЛАБОРАТОРНАЯ РАБОТА
2_9. ДИФРАКЦИОННАЯ РЕШЕТКА
Ознакомьтесь с теорией в конспекте, учебнике (Савельев, т.2, §129,130). Запустите программу «Эл-магн.Кванты». Выберите «Оптика» и «Дифракционная решетка». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).
ЦЕЛЬ РАБОТЫ:
* Знакомство с моделированием процесса сложения когерентных электромагнитных волн.
* Экспериментальное исследование закономерностей взаимодействия световых волн с периодической структурой (дифракционной решеткой).
КРАТКАЯ ТЕОРИЯ:
Зарисуйте с экрана компьютера то, что расположено в трех прямоугольных рамках.
ДИФРАКЦИОННОЙ РЕШЕТКОЙ называется совокупность большого числа N одинаковых, отстоящих друг от друга на одно и то же расстояние, прямоугольных щелей в плоском непрозрачном экране.
ПЕРИОДОМ (постоянной) дифракционной решетки называется расстояние d между серединами соседних щелей или сумма ширины щели b и ширины непрозрачного участка a.
При анализе излучения, проходящего через решетку, обычно используют линзу и экран, расположенный в фокальной плоскости линзы на расстоянии L от нее. Линза собирает параллельные лучи в одну точку на экране. Положение Х точки на экране зависит от угла падения q лучей на линзу: X = Lsin(q). Для очень малых углов sin(q) = q и X = qL.
РАЗНОСТЬ ХОДА лучей от соседних щелей D = dsin(q).
РАЗНОСТЬ ФАЗ лучей от соседних щелей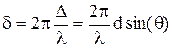 
.
ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ, идущего от решетки под углом q:
IРЕШ = I0 
,
где I0 - интенсивность, создаваемая одной щелью против центра линзы, b - ширина щели. Первый множитель обращается в 0 в точках, для которых bsin(qk) = ±kl (k = 1,2,...). Второй множитель принимает значение N2 в точках, удовлетворяющих условию dsin(qm) = ±ml (m = 0,1,2,...). Последнее условие определяет положение ГЛАВНЫХ МАКСИМУМОВ излучения, а m называется порядком максимума. Интенсивность в главном максимуме преобразуем, раскладывая синус в ряд и ограничиваясь первыми двумя членами разложения:
Im = N2I0 
.
Обозначим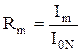 
.
Отношение Rm интенсивности в m-том максимуме к интенсивности в нулевом максимуме называется «относительной интенсивностью m-того максимума».
Формулу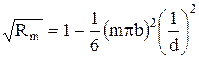 
можно проверить экспериментально и из соответствующего графика получить ширину щели.
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
Закройте окно теории. Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы и зарисуйте их в конспект.
При включении программы моделирования автоматически устанавливаются следующие параметры: порядок максимума m=1, длина волны 0.45 мкм, расстояние между щелями d = 20 мкм.
Нажимая левую кнопку мыши, установив ее маркер на дифракционной картине, меняйте m от 0 до 3 и наблюдайте изменение числового значения координаты максимума на экране. Установите длину волны излучения, соответствующую желтому цвету и, меняя m и d, снова наблюдайте картину интерференции.
