Расчет доверительного интервала ведут по формуле:
γ = ± t σ, (П1)
где t – значение критерия Стьюдента для количества степеней свободы
f = n – 1 (n – количество измерений),
σ – среднеквадратичное отклонение.
При обработке результатов определения концентрации для n повтор-
ных измерений величину σ рассчитывают по формуле:
 (П2)
(П2)
По-другому ведут расчет величины доверительного интервала исходя
из данных построения градуировочной зависимости.
Обычно эта зависимость линейна. Используя метод наименьших квад-
ратов, рассчитывают уравнение градуировочной прямой:
y = a + bх (3)
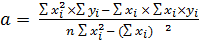 (П4)
(П4)
Если градуировочная зависимость выходит из нуля (a = 0), то формула
для расчета коэффициента b упрощается:
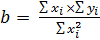 (П5)
(П5)
После этого для каждой измеренной величины аналитического сигнала
определяют разность значений Δi концентрации раствора, рассчитанных по
уравнению градуировочной зависимости C, и практически заданного значе-
ния Сi (рис. 3)
Δi = Сi – С. (П 6)
Полученные значения Δi используют для расчета среднего квадратич-
ного отклонения по формуле:
 (П7)
(П7)
A
Ai
Ci C C
Рис.3. Определение отклонений реальных значений концентрации раствора от соответствующих градуировочному графику
Затем, по формуле (П1) рассчитывают доверительный интервал для
концентрации и указывают его в качестве метрологической характеристики
результата анализа.






