Основной векторной характеристикой электростатического поля является вектор напряженности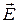 
, величина и направление которого определяется силой, действующей на единичный положительный заряд, помещенный в данную точку поля:
, В/м.
Напряженность зависит от величины заряда, формы и размеров заряженного тела, расстояния до него и от диэлектрических свойств среды. Вектор 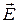характеризует результирующее поле свободных зарядов и связанных зарядов, возникающих в диэлектрике при его поляризации.
Для характеристики поля свободных зарядов (независимо от среды) используется вектор электрического смещения 
. В случае электрически изотропной среды 
, где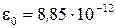 
Ф/м – электрическая проницаемость среды.
Аналогично для магнитного поля вводятся два вектора: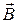 
– вектор магнитной индукции и 
– вектор напряженности магнитного поля.
Физический смысл вектора магнитной индукции можно определить из закона Ампера.
Вектор 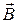численно равен максимальной силе, действующей на проводник с током в 1 А при длине 1 м.
Или: магнитная индукция в данной точке однородного магнитного поля численно равна максимальному вращающему моменту, действующему на рамку с магнитным моментом, равным единице. Единица измерения – 1 Тл (один тесла).
Вектор 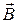характеризует суммарное поле, создаваемое проводником с током и намагниченными веществами, т.е. зависит от среды.
Для характеристики магнитного поля независимо от среды используется вектор напряженности магнитного поля .
Для однородной изотропной среды 
, где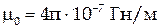 
– магнитная постоянная, 
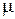– магнитная проницаемость вещества.
Изображаются магнитное и электрическое поля с помощью линий магнитной индукции и линий вектора напряженности соответственно.
Эти линии проводятся так, что в каждой точке пространства вектора 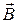(или 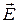) являются касательными к ним.
Для всех характеристик электрического и магнитного полей справедлив принцип суперпозиции, математическое выражение которого имеет вид 
, 
или 
.
Форма линий для отдельных тел или совокупности тел называется конфигурацией поля.
Несмотря на некоторые различия характеристик электрического и магнитного полей, существует аналогия в их математическом описании.
Использование этой аналогии позволяет упростить решение многих задач, связанных с расчетом полей.
В данной лабораторной работе метод аналогии применен для изучения магнитного поля диполя.
Электрическим диполем называют систему двух разноименных, одинаковых по величине точечных зарядов ± q, разделенных расстоянием 
, которое называют плечом диполя.
Рис. 1
Электрический момент диполя 
– это вектор, длина которого равна произведению заряда q на расстояние :
. (1)
Направлен вектор от отрицательного заряда к положительному.
Если расстояние до точки наблюдения во много раз превышает плечо диполя, то диполь называют точечным.
В аксиальной, т.е. продольной плоскости диполя, при y = 0 составляющие вектора электрической индукции точечного электрического диполя описываются следующими выражениями:
(2)
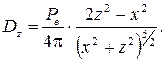(3)
На рис. 2 электрическое поле точечного электрического диполя в однородной среде изображено с помощью линий вектора . Вектора в каждой точке пространства являются касательными к изображенным линиям.
Как следует из выражений (2) и (3), вектор электрической индукции вдоль оси диполя имеет только одну составляющую 
, которая убывает с увеличением z по закону z -3.
(4)
Рис. 2
В точках пересечения линий вектора с экваториальной плоскостью (при z = 0) поле тоже имеет лишь одну составляющую :
т.е. поле в этом направлении тоже убывает обратно пропорционально кубу расстояния, но при этом вдвое меньше.
Наконец, на направлениях, определяемых соотношением
2 z 2 – x 2 = 0,
т.е. на прямых
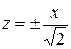, (5)
обращается в 0 и вектор имеет лишь составляющую Dx, равную
. (6)
Таким образом, и на этих направлениях поле диполя убывает обратно пропорционально кубу расстояния. Отметим, что указанные прямые (5) расположены под углами 55о и 125о относительно оси z.
Подобно тому, как в пространстве, окружающем заряженные тела, возникает электрическое поле, так и вокруг контуров с током возникает магнитное поле.
В частности, если точечный электрический диполь на рис. 1 заменить маленькой рамкой с током, называемой точечным магнитным диполем (рис. 3), то напряженность магнитного поля, рассчитываемого по закону Био-Савара-Лапласа, будет определяться формулами, аналогичными выражениям (2) и (3):
(7)
. (8)
Рис. 3
В формулах (7) и (8) 
– магнитный момент диполя, равный
= ISN, (9)
где I – ток в рамке, S – площадь рамки, N – число витков рамки.
Направлен магнитный момент так же, как магнитное поле в центре рамки, т.е. по правилу правого винта. Если контур с током имеет конечные размеры, то формулы (7) и (8) описывают магнитное поле на больших расстояниях от контура.
Таким образом, на больших расстояниях конфигурации поля вектора электрической индукции заряженного тела и вектора напряженности магнитного поля контура с током одинаковы. Численные значения и размерности различны лишь из-за отличий значений дипольных моментов Р е и Рm.
Из формул (1) и (4) следует, что вектор измеряется в 
, а из формул (9) и (8) получаем для вектора размерность А/м.
Расчет электрических и магнитных полей и определение их конфигурации необходимы при конструировании таких устройств, как излучающие антенны, радиотелескопы, ускорители заряженных частиц, электродвигатели, электрогенераторы и т.д.
