В теории цифровых устройств с памятью – теории автоматов – основными задачами являются задачи анализа и синтеза автоматов. Под анализом автомата понимают определение закона его функционирования по заданной структуре авто- мата, а под синтезом – построение автомата из более простых (элементарных) ав-томатов по заданному закону функционирования. При решении этих задач обычно выделяется несколько этапов, среди которых наиболееважными являются абстракт-ный и структурный этапы.
На абстрактном этапе под автоматом подразумевается цифровое устройст- во, задаваемое тремя непустыми множествами X ={ x l, х 2,..., хп }, Y ={ y l, y 2,..., ут }, Z = { z l, z 2, …, zl },а также двумя функциями:функцией переходов δ ифункцией выходов λ. Множества X, Y и Z называются соответственно алфавитами входных сигналов, выходных сигналов исостояний. Функция переходов δ определяет состо-яние автомата z (s+1) в зависимости от состояния z (s) и значения входной буквы x (s),т. е.
где s =0, 1, 2,... – дискретное время; z (s)и х (s) – значения букв соответствующих алфавитов в s -e моменты дискретного времени, а функциявыхода определяет зна - чение выходной буквы y (s)взависимостиотсостоянияавтомата z (s)и входнойбуквы х (s):
(20)
Абстрактный автомат реализует отображение множества слов входного ал-фавита во множество слов выходного алфавита и имеет только один входной и один выходной каналы, являясь, таким образом, лишь математической моделью реальных устройств. При построении таких моделей реальный автомат с g входами и h выходами, имеющий k 1 букв во входном алфавите и k 2букв в выходном алфа- вите, заменяется автоматом с одним входом и выходом, входной алфавит которого состоит из 
букв, а выходной из 
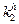букв.
На структурном этапе автомат рассматривается как структура, состоящая из элементов некоторого стандартного набора, в который входят набор элементар- ных автоматов (триггеров) и функционально полная система логических элементов. Структурный автомат, в отличие от абстрактного, имеет несколько элементарных входных и выходных каналов, по которым могут передаваться элементарные сиг- налы. Конечное множество символов, отображаемых различными элементарными сигналами и подаваемых (принимаемых) на один вход (выход) структурного авто- мата, называется структурным алфавитом. Каждый входной и выходной сигналы абстрактного автомата в структурном автомате представляются наборами букв структурного алфавита. С инженерной точки зрения наибольший интерес представ- ляет задача структурного синтеза автоматов.
Функция выходов абстрактного автомата может быть задана двумя спосо- бами. Если выходной сигнал автомата определяется выражением (20), т. е. зависит как от состояния автомата, так и от входного сигнала, то автомат называется авто- матом Мили. Если же выходной сигнал автомата не зависит от входного, а одно- значно определяется состоянием автомата
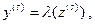
то такой автомат называют автоматом Мура.
Функции 
и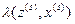 
, описывающие работу автомата Мили, задаются таблицами переходов и выходов. Столбцы таких таблиц обозначаются символами из множества Z, а строки – символами из множества X. В клетку таб- лицы переходов, находящуюся на пересечении столбца zi и строки xj, записывает- ся состояние автомата 
в которое он переходит из состояния 
под воздействием сигнала 
.В таких же клетках таблицы выходов записывается сиг- нал 
Таблицы переходов и выходов автомата Мили могут быть пред-ставлены совмещенной таблицей, вклетках которой указаны как значения функ- ции δ, так и значения функцииλ.
Более наглядным является задание автоматов Мили с помощью графов. Граф автомата состоит из узлов (вершин), соединенных ветвями (ребрами). Узлы графа отождествляются с состояниями автомата, а ветви отмечаются входными сигнала- ми х, вызывающими переход автомата из состояния zi в состояние zj и выходны- ми сигналами 
Функции переходов ивыходов автомата Муразадаются одной отмеченной таблицей переходов, которая строится также, как и таблица переходов автомата Мили, но над символами zi отмечаются символы выходных сигналов, соответствую-щих данному состоянию. На графах автоматов Мура значения выходных сигналов записываются около узлов, а ветви обозначаются лишь входными сигналами.
Иногда для задания автоматов используются так называемые квадратные автоматные матрицы (таблицы), строки и столбцы которых отмечены состояниями автомата. В клетку такой матрицы, находящуюся на пересечении i -й строки и j -го столбца, вписываются все входные сигналы, вызывающие переход автомата из сос-тояния zi в состояние zj. Для автоматов Мили каждый входной сигнал дополни- тельно отмечается соответствующим выходным сигналом. Для автоматов Мура вы-ходными сигналами отмечаются строки квадратной автоматной матрицы.
Два автомата, у которых совпадают как входные, так и выходные алфави- ты, называются эквивалентными, если для любого входного слова выходное слово одного автомата совпадает с выходным словом другого автомата при условии, что оба автомата находились в одном и том же начальном состоянии. Для любого ав- томата Мили можно построить эквивалентный автомат Мура и наоборот. Рассмот- рим алгоритмы таких переходов на примере автомата Мили, заданного табл. 9 и 10. Поставим в соответствие каждой паре (zi, zj) автомата Мили состояние zij авто-
Таблица 9 Таблица 10
| z 0 | z 1 | z 2 | z 3 | |
| x 1 | y 3 | y 2 | y 1 | y 1 |
| x 2 | y 2 | y 1 | y 3 | y 3 |
| x 3 | y 1 | y 2 | y 2 | y 3 |
| z 0 | z 1 | z 2 | z 3 | |
| x 1 | z 1 | z 2 | z 0 | z 2 |
| x 2 | z 3 | z 0 | z 0 | z 0 |
| x 3 | z 2 | z 3 | z 2 | z 3 |
мата Мура. Кроме того, во множество состояний автомата Мура включим началь- ное состояние z 0автомата Мили. Для рассматриваемого случая такое соответствие представлено табл. 11. Если автомат Мили имеет l состояний и k входных сигна-
Таблица 11
| z 0 z 00 | z 1 | z 2 | z 3 | |
| x 1 | z 1 z 01 | z 2 z 11 | z 0 z 21 | z 2 z 31 |
| x 2 | z 3 z 02 | z 0 z 12 | z 0 z 22 | z 0 z 32 |
| x 3 | z 2 z 03 | z 3 z 13 | z 2 z 23 | z 3 z 33 |
лов, то эквивалентный автомат Мура будет иметь kl + 1 состояний. Из табл. 11видно, что состояние z 0 автомата Мили совпадает с состояниями z 32, z 00, z 21, z 12, z 22 автомата Мура, т. е.
и далее
Поэтому переход автомата Миля из состояния z 0 в состояние z 1 должен соответствовать всем переходам автомата Мура из состояний z 00, z 12, z 21, z 22,, z 32 в состояние z 01, переход из z 1в z 3 должен соответствовать всем переходам автома- таМураиз z 01в z 02, z 13, z 33 и т. д. Отсюда следует, что если состояние zij входит во множество состояний, совпадающих с состоянием zr, тостолбец таблицы пере- ходов для состояния zij будет совпадать со столбцом таблицы переходов для со- стояния zr. Значения функции выходов для эквивалентного автомата Мура опреде-ляются соотношением 
при zij ≠ z 00.
Для начального состояния z00 значение выходного сигнала выбирается про-извольно. Таким образом, переходы и выходные сигналы эквивалентного автомата Мура определяются табл. 12.
Таблица 12
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
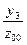
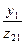
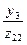
| x 1 | z 01 | z 11 | z 31 | z 21 | z 21 | z 01 | z 31 | z 01 | z 01 | z 21 | z 21 | z 01 | z 31 |
| x 2 | z 02 | z 12 | z 32 | z 22 | z 22 | z 02 | z 32 | z 02 | z 02 | z 22 | z 22 | z 02 | z 32 |
| x 3 | z 03 | z 13 | z 33 | z 23 | z 23 | z 03 | z 33 | z 03 | z 03 | z 23 | z 23 | z 03 | z 33 |
Задача перехода от автомата Мура к эквивалентному автомату Мили реша- ется очень просто. Если δ1 и λ1– функции переходов и выходов автомата Мура, то функции переходов δ2(z, x)и выходов λ2(z, x)эквивалентного автомата Мили определяются следующими соотношениями:
δ2(z, x) = δ1(z, x), λ2(z, x) = λ1(δ1(z, x)).
Следовательно, таблица переходов эквивалентного автомата Мили совпадает с таблицей переходов автомата Мура, а в каждую клетку таблицы выходов за-писывается символ, которым отмечено состояние автомата Мура в данной клетке. При таком преобразовании граф автомата Мнли отличается от графа автомата Мура только тем, что выходные сигналы из узлов графа перенесены на всеветви, входя- щие вданный узел.
Число состояний автомата существенно влияет на егосложность. Поэтому важное значение имеет определение абстрактного автомата с наименьшим возмож- ным числом состояний, реализующего заданное отображение слов входного алфа- вита в слова выходного алфавита. Рассмотрим алгоритм минимизации числа состо- яний автомата. Будем называть k -эквивалентными два состояния автомата Мили (k = 1, 2,..., ∞), если автомат, находясь в любом из них, при подаче входного слова из k букв выдает одинаковые выходные сигналы. Если состояние zi k -эквивалентно состоянию zt,a zt k- эквивалентно состоянию zj,то и zi k -эквивалент- но zj. Объединение всех k -эквивалентных состояний автомата образует класс k -экви-валентных состояний. Например, для автомата, заданного табл. 13 и 14, классы 1-эквивалентных состояний, определяемые одинаковыми столбцами таблицы выхо-
Таблица 13 Таблица 14
| z 0 | z 1 | z 2 | z 3 | z 4 | z 5 | z 6 | |
| x 1 | y 1 | y 2 | y 2 | y 1 | y 1 | y 2 | y 2 |
| x 2 | y 1 | y 2 | y 2 | y 1 | y 1 | y 2 | y 2 |
| x 3 | y 2 | y 3 | y 3 | y 2 | y 2 | y 3 | y 3 |
| z 0 | z 1 | z 2 | z 3 | z 4 | z 5 | z 6 | |
| x 1 | z 0 | z 3 | z 3 | z 6 | z 0 | z 3 | z 4 |
| x 2 | z 1 | z 2 | z 2 | z 5 | z 1 | z 2 | z 0 |
| x 3 | z 3 | z 1 | z 1 | z 4 | z 3 | z 1 | z 6 |
дов, будут следующие:
B 11 = { z 0, z 3, z 4}, B 12 = { z 1, z 2, z 5, z 6 } (21)
(первый индекс при В является степенью эквивалентности k, а второй – порядковым номером класса для данного k).
Для того чтобы из классов k -эквивалентных состояний сформировать клас- сы k + 1-эквивалентных состояний, необходимо найти классы 1-эквивалентных сос-тояний внутри каждого класса k -эквивалентных состояний. Признаком разбиения множества состояний автомата на классы ∞-эквивалентности является совпадение разбиения на классы k -эквивалентных состояний с разбиением на классы к + 1-эквивалентных состояний. Таким образом, разбиение на классы ∞-эквивалентных состояний может быть достигнуто за конечное число шагов. Если теперь из каж- дого класса ∞-эквивалентных состояний выбрать по одному состоянию, то полу- чим автомат, имеющий минимальное число состояний, равное числу классов ∞-эквивалентности, и формирующий при подаче любого входного слова те же вы- ходные сигналы, что и исходный автомат. Определим классы ∞-эквивалентных состояний для автомата, заданного табл. 13 и 14. На основе табл. 13 и выраже- ний (21) построим таблицу разбиения на классы 1-эквивалентности (табл. 15), за- меняя при этом состояния zi соответствующими классами эквивалентности. По табл. 15 получаем разбиение на классы 2-эквивалентности:
B 21 = { z 0, z 4}, B 22 = { z 3}, B 23 = { z 1, z 2, z 5}, B 24 = { z 6}. (22)
Аналогично на основе табл. 13 и выражений (22) строим таблицу разбие- ния на классы 2-эквивалентных состояний (табл. 16), из которой получаем раз-
Таблица 15 Таблица 16
| B 21 | B 22 | B 23 | B 24 | ||||
| z 0 | z 4 | z 3 | z 1 | z 2 | z 5 | z 6 | |
| x 1 | B 21 | B 21 | B 24 | B 22 | B 22 | B 22 | B 21 |
| x 2 | B 23 | B 23 | B 23 | B 23 | B 23 | B 23 | B 21 |
| x 3 | B 22 | B 22 | B 21 | B 23 | B 23 | B 23 | B 24 |
| B 11 | B 12 | ||||||
| z 0 | z 3 | z 4 | z 1 | z 2 | z 5 | z 6 | |
| x 1 | B 11 | B 12 | B 11 | B 11 | B 11 | B 11 | B 11 |
| x 2 | B 12 | B 12 | B 12 | B 12 | B 12 | B 12 | B 11 |
| x 3 | B 11 | B 11 | B 11 | B 12 | B 12 | B 12 | B 12 |
биение на классы 3-эквивалентности:
B 31 = B 21 = { z 0, z 4}, B 32 = B 22 = { z 3}, B 33 = B 23 = { z 1, z 2, z 5}, B 34 = B 24 = { z 6}.
Таким образом, разбиение множества состояний автомата на классы ∞-эк-вивалентности совпадает с разбиением его на классы 2-эквивалентных состояний. Выберем теперь из каждого класса 2-эквивалентности произвольно по одному сос-тоянию, например z 0, z 3, z 1, z 6. Заменяя в табл. 13 состояние z 4 ∞-эквивалентным ему состоянием z 0, состояния z 2 и z 5 – состоянием z 1и вычеркивая лишние столб- цы в табл. 14, получаем автомат с минимальным числом состояний (табл. 17 и 18).
Таблица 17 Таблица 18
| z 0 | z 1 | z 3 | z 6 | |
| x 1 | y 1 | y 2 | y 1 | y 2 |
| x 2 | y 1 | y 2 | y 1 | y 2 |
| x 3 | y 2 | y 3 | y 2 | y 3 |
| z 0 | z 1 | z 3 | z 6 | |
| x 1 | z 0 | z 3 | z 6 | z 0 |
| x 2 | z 1 | z 1 | z 1 | z 0 |
| x 3 | z 3 | z 1 | z 0 | z 6 |
Для минимизации числа состояний автоматов Мура необходимо дополни-тельно рассматривать классы 0-эквивалентных состояний. При этом 0-зквивалент- ными называются любые одинаково отмеченные состояния автомата Мура. Все дальнейшие классы k -эквивалентности в данном случае определяются так же, как и для автомата Мили.
В схемах ВТ часто встречаются автоматы, на входы которых некоторые последовательности сигналов никогда не подаются. 
Такие последовательности на-зываются запрещенными входными словами. Прн наличии запрещенных входных слов функции переходов и выходов будут определены не для всех пар значений z и х. Такие автоматы называются частичными автоматами. Графы частичных автоматовимеют узлы,у которых количество выходящих ветвей меньше числабукв входного алфавита.При синтезе частичного автомата производят доопределение функций переходов ивыходов стем, чтобы максимально упростить его реализа-цию.
При решении задачи структурного синтеза автомата необходимо описать условия его функционирования на некотором формальном языке, т. е. ввести стан-дартную форму задания автоматов. В качестве такой стандартной формы задания автоматов обычно используют кодирование буквами соответствующих структурных алфавитов таблицы переходов и выходов. Кроме того, задают или выбирают набор триггеров и логических элементов. В результате выполнения этапа структурного синтеза получают структурную схему автомата, т. е. способ соединения между собой триггеров и логических элементов, обеспечивающий заданные условия функ-ционирования автомата.
Используемые в цифровых устройствах триггеры являются элементарными автоматами Мура с двумя внутренними состояниями, которым соответствуют два различных выходных сигнала. Это дает возможность обозначать состояния и вы-ходные сигналы триггеров одинаковыми символами и кодировать их буквами дву-значного структурного алфавита. Входной структурный алфавит таких элементар- ных автоматов также является двузначным.
Если для каждой пары zi и zj состояний автомата найдется хотя бы один входной сигнал, переводящий его из состояния zi в состояние zj при i ≠ j и i = j, то такой автомат называется автоматом с полной системой переходов.
Если автомат Мура в каждом состоянии выдает выходной сигнал, отли-чающийся от сигналов, соответствующих другим состояниям, то такой автомат на-зывается автоматом с полной системой выходов. Все реальные автоматы Мура с двумя внутренними состояниями имеют полную систему выходов.
Набор триггеров и логических элементов называется структурно полным, если из элементов этого набора можно построить любой автомат. Для этого на- бор должен содержать функционально полную систему логических элементов, а также хотя бы один триггер с полными системами переходов и выходов.
Канонический метод структурного синтеза автоматов состоит в сведении задачи синтеза произвольных автоматов к задаче синтеза комбинационных схем. Этот метод ориентирован на использование структурно полного набора триггеров и логических элементов и на обобщенное представление структурной схемы автомата в виде, показанном на рис. 5, а.
Обобщенная схема автомата состоит из триггеров Q 1, Q 2, ..., Qm и ком-бинационной схемы F, связанных между собой так, чтобы выполнялись заданные условияработы автомата. Каждоесостояние zi синтезируемогоавтомата кодирует- ся набором состояний триггеров.
Структурный синтез сводится к построению такой схемы автомата, которая функционирует в соответствии с заданными таблицами переходов и выходов автомата. Для такого построения необходимо:
1. Поставить в соответствие каждой из букв хi и yi входного и выходного ал-фавитов абстрактного автомата совокупности букв структурного алфавита, т.е. вы-полнить кодирование входных и выходных сигналов.
2. Определить количество и выбрать типы триггеров.
3. Поставить в соответствие каждому состоянию zi абстрактного автомата со-вокупность состояний Q 1, Q 2, …, Qm триггеров (выполнить кодирование состояний автомата).
4. Найти переключательные функции q 1, q 2, …, qm и у 1, у 2,..., ут. Эти функ- ции определяют структуру комбинационной схемы F.
Рис. 5
Число r и р входов и выходов структурных автоматов, а также число т триггеров при использовании двузначного структурного алфавита определяются из условий
где п и k – соответственно число букв во входном и выходном алфавитах абст- рактного автомата, l – число состояний автомата.
Функция 
(i = 1, 2,..., т)называется функцией возбуждения триггера Qi и определяет значение входного сигнала триггера в зависимости от состояний 
триггеров и значений сигналов 
на входах автома- та, т. е.
Значения аргументов и функции в этом выражении определены для одного и того же момента дискретного времени, поэтому qi является переключательной функцией. Для триггера, имеющего несколько входов, на этапе структурного син- теза следует получить функцию возбуждения каждого его входа. Определение значений функций возбуждения i -гo триггера может быть произведено путем под-становки в его функцию переходов значений 
и 
,взя 
тых из кодирован- ной таблицыпереходов заданного автомата,и последующегорешения полученно- го уравнения относительно значений . Так какчисло различных уравнений та- кого типа равно всего 4 (для наборов 00, 01, 10, 11 состояний и ,то на практике частопользуются готовыми таблицами решения такихуравнений, назы-ваемых таблицами возбуждения триггеров. Значение может иногда оказаться неопределенным, т. е. может быть равным как 1, так и 0. В таких случаях значе- ние можно выбирать произвольно так, чтобы выполнялись условия появления допустимых комбинаций входных сигналов триггеров.
Функция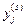 
(j = 1, 2,..., р)называется функцией выходов и определяет значение сигнала на j -м выходе автомата в зависимости от состояний триггеров и входных сигналов.
При структурном синтезе автоматов может возникнуть ситуация, когда ав-томат из состояния zi входным сигналом хr переводится в состояние zj,а из zj тем же входным сигналом хr – в состояние zi. Если длительность входного сигнала хr превышает время перехода автомата из одного состояния в другое, то, если не приняты специальные меры, автомат проскочит состояние zj,которое является неустойчивым. Следовательно, для обеспечения устойчивости состояний автомата длительность входного сигнала должна быть меньше, чем сумма времени прохож-дения сигнала по самому короткому пути в комбинационной схеме F и времени переключения триггера.
Наиболее распространенным способом обеспечения устойчивости состояний автомата является введение двойной памяти, т. е. дублирование каждого элемен- тарного автомата Qi элементарным автоматом 
(рис. 5, б). Передача информа- ции из ряда триггеров Qi в ряд происходит по сигналу Т, подаваемому во время отсутствия входных сигналов. Для формирования функций возбуждения и функций выходов автомата используются выходы . Автомат из состояния zi пе-рейдет в состояние zj лишь после передачи информации из ряда Qi вряд . По- этому во время действия входных сигналов автомат не может пропустить состоя-ние zj.
Устойчивость состояний автомата можно также обеспечить, используя две непересекающиеся во времени последовательности синхронизирующих сигналов – Т1 и Т2. Если синхронизировать переход автомата из zi в zj сигналом Т1, а пере- ход из zj в zi сигналом Т2, то эти переходы будут вызываться различными вход- ными сигналами хr Т1 и хr Т2. Однако этот способ применим лишь в том случае, когда все переходы в состояние zj могут быть синхронизированы сигналом Т1, а все переходы из z j – сигналом Т2. При этом для любого узла графа автомата все входящие ветви должны быть отмечены одним из символов Т1, Т2, а все выхо- дящие ветви – другим. В свою очередь, такую разметку графа можно всегда вы- полнить, если все замкнутые последовательности его ветвей содержат четное их число. Для графа, имеющего хотя бы одну нечетную замкнутую последователь- ность ветвей, указанную разметку осуществитьнельзя. В некоторых случаях замк-нутую нечетную последовательность ветвей можно преобразовать вчетную путем разрыва однойветви последовательности и включения в разрыв дополнительного состояния автомата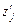 
,соответствующего нулевому выходному сигналу.
При работе автомата могут возникнуть так называемые гонки (состязания). Причиной гонок является то, что триггеры имеют различные времена переключе- ния и различна также задержка сигналов, поступающих на входы триггеров по раз-личным цепям схемы F. При переходе автомата из одного состояния в другое, сопровождающемся переключением нескольких триггеров, тот из них, который из-менит свое состояние раньше других, через схему F может изменить сигналы на входах триггеров до того,, как они переключаются. Поэтому в процессе перехода из состояния zi в состояние zj под действием входного сигнала хr автомат может ока- заться в некотором состоянии z ω,переход в которое не указан в таблице перехо- дов или на графе. Пусть, например, сигналом хr автомат, содержащий триггеры Q 1, Q 2и Q 3, переводится из состояния 011 в состояние 100. Предположим далее, что триггеры Q 2 и Q 3уже переключались, a Q 1остается в исходном состоянии. Тогда автомат окажется в состоянии 000. Если к тому же в автомате имеется пе- реход из 000, например в 010 под действием того же сигнала хr,то автомат в ре-зультате может оказаться в состоянии 010, а не в 100.
Исключить гонки можно путем введения двойной памяти. В этом случае изменение состояний автомата происходит во время отсутствия входных сигналов. Кроме того, избежать гонок можно и с помощью соответствующего кодирования состояний автомата. Способы кодирования состояний автомата, исключающие гон- ки, называются противогоночными. Предположим, что состояния автомата закодированы и состоянию zi соответствует код Ki. Обозначим через { Ki - j }множество кодов (наборов) состояний элементарных автоматов, которые могут возникнуть при переходе из zi в zj за счет неодновременного переключения последних. Например, если Ki = 0011 и Kj = 0100, то { Ki - j } = {0011, 0000, 0001, 0010, 0101, 0110, 0111, 0100}. Если для любых пар переходов автомата из zi в zj и из zs в zp,вызываемых одним и тем же входным сигналом, во множествах { Ki - j }и { Ks -p }отсутствуют одина- ковые коды, то гонки в таком автомате отсутствуют. Если же имеется хотя бы одно состояние, код которого входит как в { Ki - j },так и в { Ks - p },то гонки могут воз-никать.
Пары кодов Ki, Kj и Ks, Kp называются развязанными, если хотя бы один разряд кода принимает одно значение в паре Ki, Kj и противоположное в паре Ks, Kp. В противном случае пары кодов называются связанными. Например, пары кодов 0100, 0101 и 0000, 0001 развязаны, так как третий разряд в первой паре противо-положен третьему разряду во второй паре. Связанными являются пары кодов 0100, 0101 и 0111, 0101. Для исключения гонок в автомате необходимо и достаточно закодировать его состояния так, чтобы для любых пар переходов из zi в zj и из zs в zp,вызываемых одним и тем же входным сигналом, соответствующие пары ко- дов Ki, Kj и Ks, Kp были развязаны.
Эффективным способом противогоночного кодирования является соседнее кодирование. По этому способу любые два состояния автомата, соединенные ветвью на графе, кодируются набором двоичных цифр, отличающихся лишь в одном раз- ряде. Таким образом, при любом переходе автомата из одного состояния в другое изменяется состояние лишь одного триггера, и условие отсутствия гонок всегда бу- дет выполнено,
