Основы теории переключательных функций

На втором и третьем иерархических уровнях техни­ческие средства цифровых ЭВМ в зависимости от вида функций, описывающих их работу, принято разделять на два класса: устрой­ства комбинационного типа (комбинационные, логические, функ­циональные схемы, схемы без памяти) и конечные автоматы (цифро­вые автоматы, схемы с памятью). В устройствах комбинационного типа выходные сигналы зависят только от входных сигналов в дан­ный момент дискретного времени и не зависят от входных сигналов, действовавших в предыдущие моменты времени. В конечных ав-тома­тах выходные сигналы определяются как входными сигналами, так и состояни- ем автомата, которое, в свою очередь, зависит от вход­ных сигналов, действовавших ранее. Задача проектирования (зада­ча синтеза) для комбинационных устройств и ко-нечных автоматов решается различными методами. Математический аппарат, обес­печивающий решение задачи проектирования цифровых устройств на логическом и операционном уровнях, разрабатывается в теории переключательных функций и цифровых автоматов.

Функционирование цифровых вычислительных устройств ком­бинационного типа, имеющих п входов и т выходов, в общем случае может быть описано системой функций вида

где значение функций y_j определяют значения выходных сигналов, j = , а на- боры аргументов (х ₁, х ₂, …, х_п)соответствуют вход­ным сигналам. Как функции у_j, так и аргументы x_i могут принимать только конечное число значений (обычно x_i, у_j {0, 1}). Такие функ­ции получили название переключательных (нулевых, дву-значных, логических).

Переключательные функции чаще всего задаются с помощью таб­лиц, назы- ваемых таблицами истинности, путем перечисления их значений на всех наборах значений аргументов. С целью упрощения таблиц истинности наборы аргументов нумеруют. Номер X набора аргументов равен двоичному числу, соответствующему этому набору, т. е.

Если функция зависит от п аргументов, точисло различных наборов аргу-ментов равно 2 ⁿ, поскольку каждый набор имеетсвой номер, а общее число номе- ров равно количеству различных двоич­ных n - разрядных чисел.Двефункцииотли-чаются друг от друга,если они принимаютразличные значения хотя бы на одномнаборе аргументов. Число различных функций от п аргументов равно , так какдля задания функции f (х ₁, х ₂, …, х_п)необходимо указать набор из 2 ⁿ констант f (a ₁, a ₂, …, a_п), a_i {0, 1}, а число различных 2 ⁿ -разрядных наборов равно . В таблице истинности значения функций на некоторых наборах могут быть не определены, т. е. могут принимать как значение 0, так и значение 1. Такие функции называются частично определенными, в отличие от полностью опреде­ленных, прини-мающих значения 0 и 1 на всех наборах аргументов. Наборы, на которых функция не определена, называются несуществен­ными (фиктивными). Число переключатель-ных функций, завися­щих от одного аргумента, равно четырем, причем три из них явля­ются тривиальными (их значения либо совпадают со значениями аргумента, ли- бо не зависят от них и постоянно равны 0 или 1). Единственной нетривиальной функцией является функция отрица­ния или инверсии, которая записывается в виде f (х) = .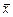

Число переключательных функций от двух аргументов равно 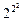= 16. Все такие функции перечислены в табл. 6. Перечислить подобным образом функции п ≥3 переменных трудно, так как их число очень быстро растет по мере увеличения

Таблица 6

	Номер X наборов (x 1, x 2)	Названия и обозначения функций
Значения функций на наборе с номером X					Константа 0
				Конъюнкция, логическое умножение, И
				Запрет по , ЗАПРЕТ
				Переменная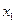
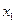
				Запрет по , ЗАПРЕТ
				Переменная
				Неравнозначность, сумма по модулю 2
				Дизъюнкция, логическое сложение, ИЛИ
				Функция Пирса, отрицание дизъюнкции, ИЛИ – НЕ
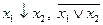
				Равнозначная эквивалентность,
				Отрицание , НЕ
				Импликация по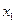
				Отрицани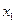е , НЕ
				Импликация по
				Функция Шеффера, отрицание конъюнкции, И – НЕ
				Константа 1

 

п. Однако среди функ­ций п переменных всегда можно указать функции, аналогичные по свойствам функциям двух переменных. К таким функциям относятся константы 0 и 1; переменные x ₁, x ₂,..., х_п;конъюнк­ция, принимающая единичное значение только на одном наборе аргументов; дизъюнкция, принимающая нулевое значение только на одном наборе аргументов; сумма по модулю 2; равнозначность; функции Пирса и Шеффера и др.

Суперпозицией переключательных функций называется подста­новка одних функций вместо аргументов в другие функции. Так как множество значений пере-ключательных функций совпадает со мно­жеством значений их аргументов, то функ-ции от большого числа аргументов могут быть представлены как суперпозиции от меньше­го числа аргументов.

Система переключательных функций, с помощью которых путем суперпозиций можно представить любую сколь угодно сложную функцию, называется функцио-нально полной. Функционально пол­ными являются следующие системы функций

Особенностью систем 6) и 7) является то, что каждая из них со­стоит только из одной функции. Системы 1) — 5) называются избы 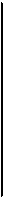точно полными системами, так как одна из функций x ₁ x ₂или может быть исключена без потери функ-циональной полноты. Интег­ральные логические микросхемы некоторой серии чаще всего реали­зуют избыточные функционально полные системы, причем не только перечисленные выше, но и получаемые путем объединения неко­торых из систем 1) — 8), дополнения их другими функциями, уве­личения числа аргументов. Пере-ключательная функция, реализу­емая интегральной микросхемой, называется также элементным ло­гическим оператором и задается в виде И—НЕ, ИЛИ, И—ИЛИ—НЕ и т. п.

Одной и той же переключательной функции могут соответство­вать различ- ные суперпозиции функций функционально полной систе­мы. В связи с этим возни- кает задача нахождения такой формы за­писи функций, при которой каждой функции будет соответствовать одна и только одна формула стандартного типа и каждой формуле стандартного типа будет соответствовать одна и только одна функ­ция. Та- кие формы записи функций называются каноническими. С по­мощью соотношения

 

 

где

любую n- местную функцию, т. е. функцию п переменных, можно разложить по переменной х ₁ на две составляющие функции, каждая из которых зависит уже от n - 1 аргументов. В свою очередь, функции f (0, х ₂,..., х_п)и f (1, x ₂,..., х_п)можно разложить по пере­менной х ₂и т. д.

Разложение функции по m переменным будет иметь вид

 

 

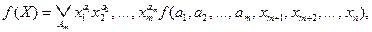
где символ означает дизъюнкции по всем наборам А_т = (a ₁, а ₂,…, а_т).При т = п получим разложение функции по всем своим аргументам:

 

(10)

где f (A) = f (а ₁, а ₂, ..., а_п).

Из выражения (10) следует, что между всеми функциями п аргументов и их представлениями в виде (10) можно установить взаимно однозначное соответствие. Поэтому выражение (10) яв­ляется канонической формой представления переклю-чательных функ­ций. Используя свойства конъюнкции, состоящие в том, что 0 х = 0, 1 х = х, выражение (10) можно переписать как

(11) где символ означает, что дизъюнкцию берут только по тем наборам А, на кото- рых f (A) = 1. Каноническая форма (11)получила название совершенной дизъюнк-тивной нормальной формы (СДНФ). Термин «совершенная» указывает на то, что дизъюнктивные члены (выражения вида )формируются из всех аргу-ментов х ₁, х ₂, ..., х_п функции f (X). Термин «дизъюнктивная» указывает на то, что внешней функцией разложения является дизъюнкция, а внутренней — конъюнкция, так как для вычисления значений функции надо сначала определить значения всех конъюнкций, а за­тем вычислить их дизъюнкцию. Термин «нормальная» указывает на то, что форма является двухуровневой, т. е. дизъюнкция конъ­юнкций.

СДНФ называется также совершенной нормальной формой (со­кращено СНФ) типа И/ИЛИ.Такое название указывает, чтов дан­ной СНФвнутренней функцией является конъюнкция (функция И), авнешней — дизъюнкция (функция ИЛИ). Очевидно, что канони­ческую форму И/ИЛИ удобно использовать для проектирова- ния устройств комбинационного типа тогда, когда интегральные микро­схемы реа- лизуют элементные операторы И, ИЛИ, НЕ. При наличии других элементных ло- гических операторов целесообразно исполь­зовать другие канонические формы, получаемые из ( 11 ) с помощью так называемых правила двойного отрицания = х иправила де Моргана:

в справедливости которых можно легко убедиться, составив табли­цы истинности левых и правых частей соответствующих выраже­ний при всех возможных значени- ях переменных х ₁и х ₂.

(12)

Здесь символ означает конъюнкцию по всем наборам А, где f (A) = 1.Каноническая форма ( 12 ) называется формой И—НЕ/И—НЕ. Ее целесообразно ис-пользовать в случае, когда микросхемы реализуют элементные операторы И—НЕ. Приме­нив к выражению (12) правило де Моргана, получим форму ИЛИ—И—НЕ

Так как то с учетом этого последнее выражение при­мет вид

(13)

Применив к выражению (13) еще раз указанное выше правило, получим форму ИЛИ – НЕ/ИЛИ

(14)

которую удобно использовать при наличии микросхем, допускаю­щих расширение их логических возможностей по уровню ИЛИ.

Для получения еще четырех канонических форм запишем в фор­ме ( 11 ) отрицание функции f (X):

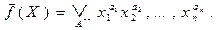
Здесь символ означает дизъюнкцию по всем наборам A, где (X) = 1, т. е.где f (X) = 0. Выполняя действия, аналогичные описанным выше,последова-тельно получим форму И—ИЛИ—НЕ

(15)

форму И—НЕ/И

(16)

форму ИЛИ/И

(17)

форму ИЛИ—НЕ/ИЛИ—НЕ

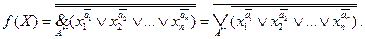(18)

Форма ( 1 7) называется также совершенной конъюнк­тивной нормальной фор-мой (СКНФ), а формы (15), (16), (18) могут быть получены путем преобразования СКНФ.

При построении канонических форм используются простейшие выражения, представляющие собой конъюнкции или дизъюнкции нескольких попарно различ- ных переменных, взятых с отрицаниями или без них. Эти выражения называются соответственно элементар­ным произведением (конъюнктивным термом) и элемен-тарной дизъюнк­цией (дизъюнктивным термом). Элементарное произведение, со- дер­жащее все переменные х ₁, x ₂,..., х_п функции и равное 1 на одном наборе ар- гументов и 0 на остальных, называется конституентой еди­ницы, или минтермом. Элементарная дизъюнкция, содержащая все переменные функции и равная 0 на одном наборе аргументов и 1 на остальных, называется конституентой нуля, или макстермом. Ис­пользование свойств дистрибутивности функций, входящих в функ­ционально полную систему, позволяет получать так называемые скобочные формы переключательных функций, у которых общие части нескольких элементарных про-изведений или дизъюнкций вы­несены за скобки. Например, для функций f ₁и f ₂, заданных таблицей истинности (табл.7), их СДНФ и не­которые из возможных скобочных форм будут следующие:

Таблица 7

x 1	x 2	x 3	f 1	f 2

 

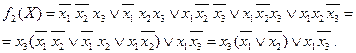
Канонические формы (11) — (18) не являются скобочными формами, так как наличие скобок здесь обусловлено лишь особенностями используемой символики.

С целью упрощения записи канонических форм переключатель­ных функций используется их числовое представление. При числовом представлении в СДНФ или СКНФ вместо конституенты 0 и 1 записываются номера наборов, на которых соответствующие кон­ституенты равны 1 (для СДНФ) или 0 (для СКНФ). Например, для функций в табл. 7

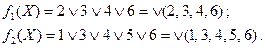
Использование цифровых ЭВМ для автоматизации процесса про­ектирова- ния аппаратных средств ВТ способствовало развитию гео­метрических форм пред-ставления переключательных функций. Каждый фиксированный набор аргументов может быть интерпрети­рован как набор координат (вектор) некоторой точки в n -мерном пространстве. Поэтому всему множеству наборов будет однознач­но соот-ветствовать множество вершин n -мерного куба (гипер­куба).

Отметив цифрами или точками вершины этого куба, где функция принимает единичные значения, получим геометрическое представле­ние переключательной функции. Набор аргументов, соответствую­щий отмеченной вершине куба, называет- ся 0-кубом. Множест­во всех 0-кубов (т. е. множество отмеченных вершин) на­зыва- ется кубическим комплексом К ⁰. Две вершины куба (два 0-куба) считаются сосед- ними, если соответствующие им наборы отличают­ся только по одной переменной. Число переменных, которые изме­няются при переходе от одного 0-куба к другому (т. е. от одной вер­шины к другой), равно расстоянию между ними. Из двух сосед- них 0-кубов можно сформировать 1-куб, в состав которого входят об­щие части 0-кубов и знак — (или X), который ставится на место изменяющейся координаты. Множество всех 1-кубов составляет кубический комплекс К ¹. Два соседних 1-куба образуют 2-куб (соседство 1-кубов определяют, считая совпадающими координа­ты, отмеченные знаком —). Все 2-кубы составляют кубический ком­плекс К ².

Аналогично определяются 3-кубы, 4-кубы и т. д., а также комплексы К ³, К ⁴и т. д. Объединение всех кубических комплек­сов К ⁰, К ¹,..., К^п называется ку- бическим комплексом К функ­ции.

Например, функции f (x ₁, х ₂, х ₃)= будут соот­ветствовать такие кубические комплексы:

 

Одна и та же переключательная функ­ция может быть представлена различ-ными суперпозициями функций функционально полной системы. Эти суперпозиции по существу являются математическими моделями цифровых вычислительных уст-ройств комбинационного типа и должны быть оптимальными по минимуму аппа-ратурных затрат на их реализацию. Количество оборудования, требуемого для реа-лизации комбинационного устройства, называется его ценой. Процесс нахождения представления функции с минимальной ценой получил название минимизации. При реализации переключательных функций элементарным произ­ведениям и дизъюнк-циям, а также и отрицаниям соответствуют некоторые достаточно простые элект- рические цепи, называемые элементами. Поэтому цена какого-либо комбинацион- ного устройства определяется как суммарное число входов всех элементов (это число называется также ценой по Квайну).

Функция называется импликантой функции f (X), если на любом наборе аргументов f (X) ≥ . Если и — импликанты функции f (X), то и дизъюнкция и также является импликантой функции f (X). Прос- той импликантой функ­ции f (X) называется такое элементарное произведение, ко- торое яв­ляется импликантой функции f (X), но никакая его собственная часть уже не является импликантой функции f (X). Под собственной частью произведения С = понимают такое произведе­ние, которое можно получить из С путем вычеркивания одной или нескольких переменных .

Любая функция имеет конечное множество простых импликант, число ко- торых не больше числа конституент 1 в СДНФ. Дизъюнкция всех простых импли- кант функции f (X) равна этой функции и назы­вается сокращенной дизъюнктив- ной нормальной формой (ДНФ). Каждая функция имеет единственную сокращен- ную ДНФ. Один из методов получения сокращенных ДНФ основан на применении операций неполного склеивания и поглощения . Для по- лучения сокращенной ДНФ функции f (X)необходимо в СДНФ функции f (X)про-извести все воз­можные операции неполного склеивания, а затем все возможные операции поглощения.

Произвести все возможные операции склеивания можно следу­ющим образом. Каждая конституента 1 сравнивается с остальными. Если конституента В отличается от конституенты С только наличи­ем отрицания у одной из переменных, то кэтим конституентам при­меняется операция склеивания, т. е. выписывается их общая часть. В результате получается группа элементарных произведений, состо­ящих из п — 1 переменных. Описанный процесс повторяется до тех пор, пока не будет получена группа, к любым двум членам ко­торой уже нельзя применить операцию склеива-ния.

Функция накрывается функцией f (X), если на любом наборе А

В общем случае сокращенная ДНФ не является минимальной, так как неко-торые простые импликанты могут накрываться дизъ­юнкцией других членов и их можно исключить. Минимальная ДНФ (МДНФ) должна состоять исключительно из простых импликант.

Нахождение МДНФ функции f (X)сводится к выделению неко­торого числа простых импликант данной функции из всего их мно­жества. Один из методов ре- шения этой задачи основан на примене­нии импликантной таблицы (матрицы). Рас-смотрим построение такой матрицы для функции f ₂(X)в табл. 7. В импликантной таб­лице 8 столбцы отмечаются конституентами 1, а стро­ки — простыми импли-кантами. В строке против каждой простой импликанты ставятся знаки X под теми конституентами, которые поглощаются данной импликантой. Непосредственно из таблицы выписываются все тупиковые ДНФ, у которых ни один из дизъюнктив- ­ных членов исключить нельзя. В тупиковую ДНФ должны войти все импликанты, отмеченные только одним знаком X,а также ми­нимальное число простых импли- кант, на пересечении которых с любой конституентой есть хотя бы один знак X. Подсчитывая число букв в тупиковой форме, определяют минимальную ДНФ.

Таблица 8

		Конституенты 1
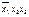
Простые Импликанты		X	X
	X			X
			X	X
			X		X

 

 

1.2

1.4

3.4

3.5

 

Из табл. 8 видно, что у функции f ₂(X)имеется две тупиковые ДНФ,каждая изкоторых содержит одинаковое число букв (т. е.каждая является МДНФ):

 

Процесс отыскания простых импликант и МДНФ можно совмес­тить. Для этого составляют таблицу, столбцы которой отмечаются конституентами. Сравнивая конституенты друг с другом, получают первую группу импликант. Каждой импли-канте соответствует от­дельная строка. Произведя в первой группе импликант все возмож­ные склеивания, получают вторую группу импликант и т. д.

 

 

Рис. 4

Эффективный способ нахождения МДНФ при небольшом числе (не более 6) переменных состоит в применении так называемых диа­грамм Вейча, являющихся разновидностью таблиц истинности.

На рис. 4 показаны диаграммы Вейча для функций двух, трех, четырех, пя- ти и шести аргументов. Каждому набору значений аргументов соответствует одна клетка диаграммы Вейча. Если на данном наборе аргументов функция равна 1, то в соответствующей данному набору клетке записывается 1. Клетки, соответствующие наборам, на которых функция равна 0, либо заполняются нулями, либо оставляются пустыми. Наборам (0, 0), (0, 0, 0),... и конституен­там соответ- ствуют клетки с номером 0, наборам (0, 1), (0, 0, 1),... и конституентам — клетки с номером 1, на­борам (1, 0), (0, 1, 0),... и конституен- там — клетки с номером 2 и т. д.

Аналогично могут быть построены диаграммы для большего чис­ла аргумен-тов. Однако из-за того, что в этом случае алгоритм поис­ка минимальных ДНФ су-щественно усложняется, диаграммы для семи и более аргументов не получили рас-пространения на практике.

Операция склеивания может быть применена только к конститу­ентам (в об- щем случае элементарным произведениям), у которых все буквы, за исключением одной, совпадают. Например, можно склеить с ,но нельзя склеить с . Такие конститу енты называются соседними. Из распределения конститу- ент на диа­граммах Вейча для п = 2, 3, 4 следует, что все соседние конституенты имеют на диаграмме соседние клетки. Исключение состав­ляют клетки, расположен- ные у границ диаграммы. Для устранения этого исключения условно отождеств- ляют противоположные гра­ницы (верхнюю с нижней и левую с правой) диаграммы, т. е. ди­аграмму мысленно сворачивают. Любым двум соседним клеткам со­ответст- вует элементарное произведение, являющееся общей частью соответствующих двух конституент и имеющее на одну букву мень­ше. Любым четырем соседним ячейкам соответствует элементарное произведение, являющееся общей частью соответст-вующих четы­рех конституент и имеющее на две буквы меньше и т. д. Поэтому склеивать можно соседние две, четыре, восемь, шестнадцать и т. д. единиц на диаграмме Вейча, а отыскание минимальной ДНФ сво­дится к определению мини-мального числа наиболее коротких эле­ментарных произведений, накрывающих все единицы на диаграмме данной функции. При п = 5, 6 отыскание простых импли- кант на диаграммах Вейча требует некоторого навыка, так как здесь не все склеивающиеся конституенты занимают соседние клетки (например, конституенты 2 и 0, 4 и 6 при n = 5; 4 и 0, 5 и 2 при n = 6). На рис. 4, е приведена диаграмма Вейча функции f ₁(X)из табл. 7, из которой следует

Задача минимизации функций, представленных в геометрической форме, часто формулируется как задача отыскания покрытия функ­ции, имеющего мини-мальную цену по Квайну. Пря этом покрытием переключательной функции назы- вается множество М кубов ком­плекса К таких, что каждая вершина комплекса К ⁰ включена по крайней мере в один куб множества M. Куби­ческий комплекс К ⁰представляет собой множество конституент пе­реключательной функции от п аргу-ментов, кубический комплекс К ¹— множество импликант, имеющих n – 1 букв, комплекс К ² — множество импликант, имеющих п – 2 букв и т. д. Комплекс же К представляет собой все множество конституент и импликант данной функции. Поэтому поиск минимального покрытия может произво­диться теми же методами, что и при использовании аналитических представлений переключательных функ- ций (с помощью импликантных матриц, диаграмм Вейча и др.) с учетом лишь особенностей двоичной числовой нумерации наборов. Известны такие методы (например, метод Рота), специально разработанные для минимиза­ции на ЭВМ гео-метрических представлений переключательных функций.

Получение минимальных форм функций, заданных канониче­скими формами (11) — (18), может быть сведено к нахождению МДНФ функции или ее отрицания. Канонические формы (11) — (14) были получены из СДНФ функции путем при- менения правила де Моргана. Но применение правила де Моргана не изменяет числа букв. Поэтому, если функцию предварительно представить в СДНФ, найти МДНФэтой функции, то, используя затем правило де Морга­на, можно получить искомую минимальную форму. Канонические формы (15) — (18) получены из отрицания функции. Поэтому для получения минимальных форм, соответствующих этим канониче­ским формам, необходимо найти МДНФ отрицания функции, исходя из которой, с помощью правила де Моргана, можно получить иско­мую минималь- ную форму.

При проектировании комбинационных вычислительных устройств с исполь-зованием микросхем малой степени интеграции наиболее важной с инженерной точки зрения является задача синтеза комбинационных схем с п входами и одним выходом из микросхем, реализующих элементные операторы И, ИЛИ, НЕ и их ком­бинации — И–НЕ, ИЛИ–НЕ, И–ИЛИ–НЕ и т. д. При этом ком­бинационной схемой называется совокупность логических элементов, реализующих заданную сис-тему переключательных функций и со­единенных по правилам, которые соответст-вуют суперпозиции функций. Цепью называется упорядоченная последователь-ность элементов, у которых хотя бы один вход соединен с выходом преды­дущего элемента. Петлей называется замкнутая цепь, по которой сигнал с выхода i- гоэле-мента непосредственно или через другие элементы может поступать на вход того же i -ro элемента. Общим свойством комбинационных схем является отсутствие пе-тель. Если же схемы, составленные из логических элементов, имеют петли (ина­че такие схемы называются схемами с обратными связями), то их функционирование не может быть полностью описано системой пе­реключательных функций. Обычно указанная выше задача синтеза решается в несколько этапов. На первом этапе под-лежащая реа­лизации переключательная функция или ее отрицание (в зависи­мости от типов логических элементов и, следовательно, от типа используемой канонической формы) представляется в СДНФ. За­тем находится МДНФ функции. На втором этапе МДНФ функции представляют в виде суперпозиции элементных логических опера­торов. На третьем этапе по операторному представлению переклю­чательной функции составляют искомую комбинационную схему. Такая последовательность и содержание этапов обеспечивает макси­мум быстродействия комбинационных схем.

Целью первого этапа синтеза является получение минимальной ДНФ задан- ной функции или ее отрицания. Подлежащая реализа­ции переключательная функ- ция f (X) может быть задана не на всех 2 ^п наборах аргументов х ₁, х ₂, ..., х_n ,т. е. может быть неполностью определенной. На тех наборах, где функция не опреде- лена, ее оп­ределяют так, чтобы соответствующая ей комбинационная схема была наиболее простой.

Достичь этого можно различными способами. Один из них состо­ит в том, что сначала не полностью определенную функцию прирав­нивают 1 на всех тех на-борах, на которых она не определена. Для полученной таким путем функции находят все ее простые импликанты. Затем с помощью импликантной матрицы оп-ределяют наименьшее число наиболее коротких простых импликант, которые на-крывают всеконституенты функции , полученной из исходной путем при-равнивания ее 0 на всехнаборах, на которых исход­ная функция не определена. Дизъюнкция найденных простыхимпликант будет соответствовать МДНФоптимально доопределенной функции. Такой метод является универсальным, однако при ма- лом числе (3—4) переменных для этого более удобнее пользоваться ди­аграммами Вейча.

На втором этапе синтеза задача представления функции в виде суперпози- ций операторов логических элементов при достаточном числе входов элементов решается так, как было показано ранее. Если же число входов элементов не до- статочно для реализации функ­ции по ее МДНФ (или по другой минимальной форме), то произво­дят группировку переменных в соответствии со следующими соот­ношениями, выражающими свойство ассоциативности логических операций дизъюнкции и конъюнкции:

Здесь символ 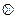обозначает дизъюнкцию или конъюнкцию; р — число входов логических элементов, а т выбирается таким, чтобы n – тр ≤ р.

На третьем этапе синтеза вначале по операторному представле­нию функции составляют первый вариант комбинационной схемы. При этом могут возникать ситуации, когда суммарное число входов элементов (или микросхем), подключен- ных к выходу некоторого элемента, превышает его нагрузочную способность (т. е. элемент перегружен). Для устранения перегрузок применяется дублирование элементов, когда каждый перегруженный элемент заменяется двумя, тремя и т. д. параллельно включенными элементами с разделенными нагрузками. Кроме того, устранять перегрузки можно путем под­ключения к выходу перегруженного элемен- та инвертирующего или неинвертирующего усилителя (обычно одного или двух элементов НЕ). В первом случае все дальнейшие схемные построения должны быть выполнены с учетом инверсии сигналов на выходе элемента. Следует иметь в виду, что дублирование увеличивает нагрузку на предыдущие элементы. Это, в свою очередь, может вызвать не­обходимость дублирования этих элементов и т. д. Использование усилителей не приводит к увеличению числа элементов на всех уров­нях схемы, однако вносит дополнительную задержку в распростра­нение сиг- налов. Поэтому оптимальным способом разгрузки являет­ся комбинированный: там, где это допустимо по быстродействию, вводят усилители, а остальные перегружен- ные элементы дублируются.

Решение задачи синтеза комбинационных схем со многими вы­ходами может быть сведено в принципе к синтезу схем с одним выходом. Для этого достаточно каждую из функций системы, описыва­ющей схему, реализовать отдельно. Однако при этом не учитывается то, что реализуемые функции зависят от одних и тех же аргумен­тов. Вследствие этого их представления в виде МДНФ или МКНФ могут содержать одинаковые члены, реализация которых при таком подходе будет повто-ряющейся.

Методы синтеза схем со многими выходами, позволяющие избе­жать пов-торения элементов одинакового назначения, разделяются на две группы. К первой группе относятся методы, использующие нор­мальные (двухуровневые) каноничес- кие формы функций. Ко вто­рой группе относятся методы, использующие мно-гоуровневые пред­ставления функций. Один из методов первой группы основан на совместной минимизации системы функций. Будем называть прос­той импликантой системы функций

(19)

такое элементарное произведение, которое является импликантой каждой из функ- ций системы, но никакая его собственная часть уже не является импликантой хотя бы для одной из этих функций. При совместной минимизации находят все простые импликанты всех возможных совокупностей функций из данной системы. Например, если минимизируется система функций (19), то сначала находят все простые импликанты каждой функции системы. Затем из функ­ций системы обра- зуют все возможные подсистемы, состоящие из двух функций. Для каждой из полученных подсистем функций находят все простые импликанты. Затем обра- зуют всевозможные подсистемы из трех функций и т. д. Множество простых импликант системы функций совпадает со множеством простых импликант функций вида

Поэтому первый этап минимизации системы функций (19) сводится к на-хождению простых импликант функций

число которых равно 2 ^т – 1.

На втором этапе минимизации из полученных простых импли­кант путем перебора различных вариантов отыскиваются наиболее простые формулы для пред-ставления функций системы. Отыска­ние таких формул удобно производить с по- мощью импликантных матриц для систем функций, которые аналогичны соответ-ствующим матрицам для одной функции. По импликантной матрице выбирают систему простых импликант, которая поглощает все конституенты всех функций системы. Такая система простых импликант называется полной. Из всех полных систем импликант выбирается та, которая содержит наименьшее число букв (так называемая ми­нимальная полная система), а из импликант такой системы обра­зу- ются дизъюнктивные формы функций.

В случае, когда функции, описывающие работу комбинационной схемы, яв-ляются неполностью определенными, образуют две систе­мы функций. Первую сис-тему получают путем приравнивания 1зна­чений функций на тех наборах, на кото- рых они не определены. Вто­руюсистему получают путем приравнивания 0 зна- чений функций на тех же наборах аргументов. Далее находят все простые импли- канты всех возможных совокупностей функций первой системы. Из найденных простых импликант и конституент второй системы со­ставляют импликантную мат-рицу для системы функций, с помощью которой формируют МДНФ оптимально доопределенных функций заданной системы. Доказательство оптимальности данного метода основано на том, что наиболее короткие простые импликанты будут у пер- вой системы, а наименьшее число конституент, необходимое для ДНФ функций, будет содержать вторая система.

Второй и третий этапы синтеза комбинационных схем со многи­ми выхода- ми аналогичны соответствующим этапам синтеза схем с одним выходом.

Наиболее распространенный метод синтеза схем, относящийся ко второй группе, получил название метода каскадов. В основе метода лежит формула раз-ложения функций

.

В свою очередь, к функциям и приме-няют эту же формулу до тех пор, пока в результате очередно­го разложения не бу- дут получены переменные или их отрицания. При этом одновременно можно по- лучать операторные представления функций.

Поскольку метод каскадов использует многоуровневые представ­ления функ-ций, задержка сигналов, обусловленная конечностью времени переключения реаль- ных логических элементов, будет больше, чем у схем, построенных по первому ме-тоду. Однако метод каскадов дает более простые схемы, так как учиты­вает ассо-циативные свойства реализуемых функций.