Рассмотрим электрическую схему, изображённую на рис.3.24. Пусть 
.
Рис.3.24. Электрическая схема трёхфазной системы, соединённой треугольником, с отключенным линейным проводом
При обрыве линейного провода Аa вектор тока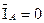 
. Преобразуем схему рис.3.24 в схему рис.3.25.
Рис.3.25. Преобразование трёхфазной электрической схемы, соединённой треугольником, с отключенным линейным проводом в однофазную электрическую схему
Из преобразованной схемы следует:
, 
, 
. (3.18)
По первому закону Кирхгофа:
; 
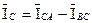. (3.19)
Используя формулы (3.18) и (3.19), построим векторную диаграмму:
Рис.3.26. Векторная диаграмма токов преобразованной схемы
3.6. Мощность трёхфазной цепи
При симметричной нагрузке активная мощность трёхфазной цепи равна сумме активных мощностей фаз: P = 
. Активную мощность трёхфазной цепи можно выразить через фазные значения напряжения и тока:
P = 
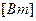. (3.20)
При соединении звездой соотношения между фазными и линейными напряжениями и токами равны: 
, 
. При соединении треугольником эти соотношения равны: 
= 
, 
. В обоих случаях 
. Тогда активную мощность можно выразить через линейные значения напряжения и тока:
P = 
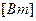. (3.21)
Реактивная мощность трёхфазной цепи
Q = 
= 
. (3.22)
Полная мощность трёхфазной цепи
S = 
. (3.23)
При расчётах удобно пользоваться следующими формулами:
; 
; 
= 
; = 
; 
= 
.
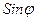При несимметричных нагрузках, соединённых звездой или треугольником, активную мощность рассчитывают по формулам:
;
.
