Методические указания к проведению лекционного занятия
Тема № 7.5. Теоремы сложения и умножения. Условная вероятность
План:
1. Совместные события
2. Теорема сложения
3. Условная вероятность
4. Теорема умножения
Совместные события
Определение. Два события А и В называются совместными, если появление одного из них не исключает появления другого при одном и том же испытании.
Пример. Стохастический эксперимент: бросание игрального кубика. События А={выпало четное число очков} и B={выпадение «4»} являются совместными. Выпадение «4» означает появление события А, а выпадение четного числа очков не исключает появление «4» при этом.
Теорема сложения
Теорема сложения. Вероятность появления хотя бы одного из совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Р(А+В)=Р(А)+Р(В)-Р(АВ)
Доказательство. Представим событие А+В в виде суммы несовместных событий.
Ω 
А В\А
На диаграмме Эйлера-Венна видно, что А+В=А+В\А=А+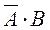 
. Так как события А и 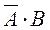- несовместны, то
Р(А+В)=Р(А)+Р(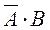) (1).
Найдем Р(В). Событие В=А·В+ .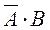
Ω
А
А·В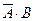 
События А·В и 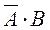- несовместны, а значит, Р(В)=Р(А·В+ 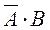)=Р(А·В)+Р(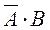). Отсюда
Р(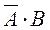)=Р(В)-Р(А·В) (2).
Подставляя (2) в (1) получим Р(А+В)=Р(А)+Р(В)-Р(А·В).
Пример. Два орудия стреляют по цели одним залпом. Вероятность попадания первого орудия р1=0,7, вероятность попадания второго орудия р2=0,8. Найти вероятность того, что хотя бы одно из орудий попадет.
Решение. Введем событие А={хотя бы одно из орудий попадет}. Событие А можно представить как сумму событий А1={попало первое орудие} и А2={попало второе орудие}: А=А1+А2.
Но события А1 и А2 могут произойти одновременно, то есть являются совместными, а значит, по теореме сложения Р(А)=Р(А1+А2)=Р(А1)+Р(А2)-Р(А1·А2)=р1+р2-р1·р2=0,7+0,8-0,7·0,8= =0,94.
