При нагружении осевой силой:
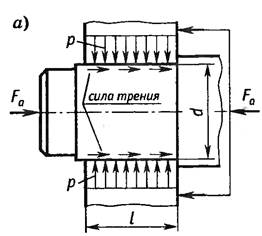
Условие несдвигаемости - 
и, вводя коэффициент запаса s, получаем:
При нагружении крутящим моментом:
Условие несдвигаемости 
, и, вводя коэффициент запаса s, получаем:
При одновременном нагружении крутящим моментом и осевой силой расчет ведут приближенно по равнодействующей силе от окружной силы 
и осевой силы, 
.
Тогда потребное давление будет 
22. Связьдавления на контактной поверхности с расчетным натягом соединения.
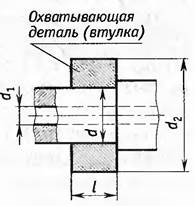
Для определения напряжений и деформаций толстостенных труб, нагруженных внутренним и внешним давлением, в курсе «Сопротивление материалов» рассмотрено решение задачи Ламе. Это решение получено с допущениями: длина трубы существенно больше ее радиуса (рассмотрена плоская задача), материал трубы однороден, поверхности контакта идеально гладкие. Однако наличие шероховатостей на поверхностях реальных деталей оказывает существенное влияние на величину расчетного натяга N. Используя решение Ламе для расчета соединений с натягом, получают связь натяга N с давлением р на поверхности стыка деталей
Где N – расчетный натяг, мкм, C1 и C2 – коэффициенты.
Где d – посадочный диаметр соединения, d1 – диаметр отверстия в охватываемой детали, d2 – наружний диаметр охватывающей детали, E1, E2, μ1, μ2 – соответственно модули упругости и коэффициенты Пуассона.
