Теория метода. Исходя из (9) смещение частицы в плоскости xOy равно = + = . , (11)

Исходя из (9) смещение частицы в плоскости xOy равно = + = .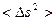

,

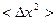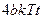(11)

где .

Проверим выполнение формулы Эйнштейна (11) на опыте. Получим значения 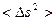для различных t и построим график, на котором ординатами точек будут значения 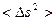, а их абсциссами – длительности промежутков времени t, в течение которых проводилось данное усреднение. Прямая пропорциональная зависимость между этими величинами подтвердит справедливость формулы Эйнштейна.

Для каждого нового значения t нет необходимости делать свою выборку смщений Δ s. Получив лишь одну выборку координат положения частицы через равные промежутки времени t (предположим, мы сделали п измерений), в качестве значений t можно взять, например, следующие значения: t₁ = t, t₂ =2 t, t₃ =3 t, t₄ =4 t. Тогда соответствующие значения среднеквадратичных смещений частицы 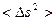из начального положения будут вычисляться так, как указано в Таблице 1.

Таблица.1 Пример обработки результатов измерений.

t = t	t =2 t	t =3 t
Сочетания координат частицы	Δ S	(Δ S)2	Сочетания координат частицы	Δ S	(Δ S)2	Сочетания координат частицы	Δ S	(Δ S)2
1-2	Δ S 12	(Δ S 12)2	1-3	Δ S 13	(Δ S 13)2	1-4	Δ S 14	(Δ S 14)2
2-3	Δ S 23	(Δ S 23)2	2-4	Δ S 24	(Δ S 24)2	2-5	Δ S 25	(Δ S 25)2
3-4	Δ S 34	(Δ S 34)2	3-5	Δ S 35	(Δ S 35)2	3-6	Δ S 36	(Δ S 36)2
4-5	Δ S 45	(Δ S 45)2	4-6	Δ S 46	(Δ S 46)2	4-7	Δ S 47	(Δ S 47)2
5-6	Δ S 56	(Δ S 56)2	5-7	Δ S 57	(Δ S 57)2	5-8	Δ S 58	(Δ S 58)2
6-7	Δ S 67	(Δ S 67)2	6-8	Δ S 68	(Δ S 68)2	6-9	Δ S 69	(Δ S 69)2
...	...	...	...	...	...	...	...	...
...	...	...	...	...	...	(n -3)- n	Δ S n -3,n	(Δ S n -3,n)2
...	...	...	(n -2)- n	Δ S n -2,n	(Δ S n -2,n)2
(n -1)- n	Δ S n -1,n	(Δ S n -1,n)2
		Σ(Δ S)2=			Σ(Δ S)2=			Σ(Δ S)2=