Броуновское движение – непрерывное, беспорядочное перемещение малых частиц вещества, взвешенных в жидкости или газе, - представляет собой одно из наиболее ярких и доступных наблюдению подтверждений основных положений молекулярно-кинетической теории вещества.
Взвешенная в жидкости, броуновская частица совершает хаотическое движение под действием ударов молекул. Вследствие их хаотического движения, импульс, передаваемый частице за макроскопически малый промежуток времени, является случайной величиной. Следовательно, случайной величиной будет и сила 
, действующая на частицу. Согласно второму закону Ньютона, уравнение движения частицы имеет вид
| (1) |
Сила возникает вследствие ударов молекул, и поскольку частица движется, то в направлении противоположном движению она получает в среднем больше ударов, чем с обратной стороны. Поэтому силу необходимо представить в виде двух слагаемых: 
- случайной силы со средним значением равным нулю < > = 0, и силы вязкого трения пропорциональной скорости частицы.
Следуя Эйнштейну 
где b – подвижность частицы.
| (2) |
Для шарообразной частицы подвижность была теоретически вычислена Стоксом:
где η – вязкость жидкости, a – радиус частицы.
Уравнение движения (2) в проекции на некоторое направление х будет
 или 
| (3) |
Очевидно, что средние значения проекций ускорения 
и силы 
равны нулю. Умножим все члены уравнения (3) на х:
|
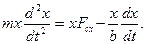
Используя очевидные равенства 
и 
выражение (3) приводим к виду
| (4) |
Если предположить, что к системе броуновских частиц применима эргодическая гипотеза, то можно провести усреднение выражения (4) по ансамблю частиц. Поскольку операции усреднения и дифференцирования коммуникативны (перестановочны), то получим
| (5) |
Вследствие того, что броуновская частица находится в тепловом равновесии со средой, то по теореме о равнораспределении энергии по степеням свободы, 
. Кроме того, поскольку смещение x частицы и сила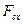 
являются независимыми случайными величинами, то 
. Обозначив 
в (5) получим неоднородное дифференциальное уравнение
| (6) |
общее решение которого имеет вид
| (7) |
где 
– значение 
в начальный момент времени, которое можно положить равным нулю. С учетом этого, из (7) следует
|
и
| (8) |
Если 
, то разложив экспоненту в ряд Маклорена до второго члена включительно, получим
|
Т.е. при малых промежутках времени t броуновская частица движется равномерно со средней скоростью теплового движения. При 
из (8) следует, что
| (9) |
Так как r2= x2+ y2+ z2, то < r2 > =< x2 > +< y2 > +< z2 >, вследствие изотропности броуновского движения < x2 > =< y2 >=< z2 >. Поэтому
| (10) |
Таким образом, средний квадрат смещения броуновских частиц пропорционален времени t наблюдения (формула Эйнштейна).
