ЗАДАЧА 1. Система состоит из трех частиц, массы которых m 1 = 0,1 г; 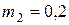 г; m 3 = 0,3 г. Первая частица находится в точке с координатами (1,2,3), вторая – в точке (2,3,1), третья – в точке (3,1,2) (координаты даны в сантиметрах). Определить радиус-вектор
г; m 3 = 0,3 г. Первая частица находится в точке с координатами (1,2,3), вторая – в точке (2,3,1), третья – в точке (3,1,2) (координаты даны в сантиметрах). Определить радиус-вектор  центра масс системы.
центра масс системы.
| ДАНО: m 1 = 1×10–4 кг; m 2 = 2×10–4 кг m 3 = 3×10–4 кг; А (1,2,3), см В (2,3,1), см; С (3,1,2), см |
 –? –?
|
АНАЛИЗ. Механическая система состоит из трех материальных точек, для которых заданы массы и их радиус-векторы. Требуется определить положение центра масс системы, записав формулу для его радиус-вектора.
РЕШЕНИЕ. Радиус-вектор центра масс механической системы определяется выражением
 ,
,
где  – радиус-векторы, проведенные из начала координат в точки А, В и С. В скалярной форме это уравнение принимает вид:
– радиус-векторы, проведенные из начала координат в точки А, В и С. В скалярной форме это уравнение принимает вид:
 ;
;  ;
;  .
.
Размерность выражения очевидна. Подставляя численные значения, получаем: xc = 14/6 см; yc = 11/6 см; zc = 11/6 см, тогда  (см).
(см).
ОТВЕТ:  (см).
(см).
ЗАДАЧА 2. Система состоит из двух тел. Известны зависимости от времени импульсов этих тел:  ,
,  .
.
а) Сохраняется ли импульс системы? б) Сохраняются ли какие-либо проекции этого импульса на декартовы оси координат? в) Чему равна результирующая внешних сил, приложенных к телам?
ДАНО:
 , кг×м/с , кг×м/с
 , кг×м/с , кг×м/с
|
а)  ?
б) ?
б)  ?
в) ?
в)  –? –?
|
АНАЛИЗ. Полный импульс механической системы сохраняется, если система замкнутая, т. е. векторная сумма внешних сил равна нулю. В этом случае, как следует из основного уравнения динамики, производная импульса по времени должна быть равна нулю. Проекция импульса на какую-либо координатную ось сохраняется, когда ее производная по времени равна нулю.
РЕШЕНИЕ. Результирующий импульс системы равен векторной сумме импульсов тел:

Взяв производную от  , получаем:
, получаем:  – полный импульс системы не сохраняется.
– полный импульс системы не сохраняется.
Из последнего выражения видно, что составляющие производной импульса на осях X, Y отличны от нуля. Таким образом, проекции импульса на ось Z сохраняется.
Результирующая внешних сил, действующих на систему, равна:
 .
.
Правильность формулы по размерности очевидна.
ОТВЕТ: а) полный импульс системы не сохраняется; б) проекция импульса на ось Z сохраняется; в)  (Н).
(Н).
ЗАДАЧА 3. Имеется система трех тел. Импульсы двух из них в некоторый момент времени в системе центра масс 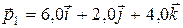 и
и  . Найти импульс
. Найти импульс  третьего тела в тот же момент времени.
третьего тела в тот же момент времени.
ДАНО:
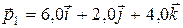 , кг×м/с , кг×м/с
 , кг×м/с , кг×м/с
|
 –? –?
|
АНАЛИЗ И РЕШЕНИЕ. В системе центра масс полный импульс равен нулю:  , отсюда:
, отсюда:
 .
.
Правильность формулы по размерности очевидна.
ОТВЕТ:  .
.
ЗАДАЧА 4. После абсолютно упругого соударения тела массой  , двигавшегося поступательно, с покоившимся телом массой
, двигавшегося поступательно, с покоившимся телом массой  оба тела разлетаются симметрично относительно направления вектора скорости первого тела до удара. Определить, при каких значениях п =
оба тела разлетаются симметрично относительно направления вектора скорости первого тела до удара. Определить, при каких значениях п =  /
/  это возможно (рис.1.3.1).
это возможно (рис.1.3.1).
ДАНО:
 (кг); (кг);  (кг)
п = (кг)
п =  / / 
|
 –? –?
|
АНАЛИЗ. В задаче рассматривается абсолютно упругое соударение двух тел. Условия, при которых происходит соударение, не оговорены. Поэтому будем считать, что на рассматриваемую систему тел не действуют внешние силы, т. е. система замкнутая. Ее импульс сохраняется. Удар абсолютно упругий, следовательно, кинетическая энергия остается постоянной.
 Рис. 1.3.1
Рис. 1.3.1
|
РЕШЕНИЕ. По закону сохранения импульса  .
.
Полный импульс системы до удара равен импульсу первого тела до удара  . Полный импульс системы после удара
. Полный импульс системы после удара  , где
, где  и
и  скорости тел после удара. Таким образом, закон сохранения импульса имеет вид:
скорости тел после удара. Таким образом, закон сохранения импульса имеет вид:
 (1.3.1)
(1.3.1)
Удар центральный, прямой, абсолютно упругий. В этом случае полная кинетическая энергия тел сохраняется:
 (1.3.2)
(1.3.2)
Спроектируем векторное уравнение (1.3.1) на координатные оси (рис. 1.3.1), получаем:
 (1.3.3)
(1.3.3)
Отсюда  , и
, и  , или
, или
 . (1.3.4)
. (1.3.4)
Из условия задачи 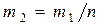 , тогда из (1.3.2) имеем
, тогда из (1.3.2) имеем
 , или
, или  тогда
тогда  .
.
Окончательно имеем  (1.3.5)
(1.3.5)
Выражения (1.3.4) и (1.3.5) составляют систему двух уравнений

Квадрат первого уравнения, отнесенный ко второму  , отсюда
, отсюда
 и
и  (1.3.6)
(1.3.6)
Проверка размерности не требуется.
Если  , то
, то 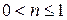 , в этом случае
, в этом случае  , и
, и  , тогда
, тогда  . Следовательно, угол, образованный скоростью любого из тел после удара и вектором
. Следовательно, угол, образованный скоростью любого из тел после удара и вектором  , удовлетворяет условию:
, удовлетворяет условию:  .
.
Если  , то
, то  и
и  . В этом случае
. В этом случае  .
.
Из выражения (1.3.6) видно, что наибольшее значение  , при котором возможен симметричный разлет тел,
, при котором возможен симметричный разлет тел,  . При этом
. При этом  и
и  – оба тела после удара движутся по направлению вектора
– оба тела после удара движутся по направлению вектора  .
.
ОТВЕТ:  .
.
ЗАДАЧА 5. Граната брошена под углом 45° к горизонту со скоростью  = 20 м/с. Через 2,0 с после бросания граната разрывается на два осколка, массы которых относятся как 1:2. Меньший осколок в результате взрыва получил дополнительную скорость
= 20 м/с. Через 2,0 с после бросания граната разрывается на два осколка, массы которых относятся как 1:2. Меньший осколок в результате взрыва получил дополнительную скорость  = 50 м/с, направленную горизонтально. Определить дальность полета большего осколка, если известно, что меньший осколок упал на расстоянии
= 50 м/с, направленную горизонтально. Определить дальность полета большего осколка, если известно, что меньший осколок упал на расстоянии  = 83 м от места броска. Сопротивление воздуха не учитывать.
= 83 м от места броска. Сопротивление воздуха не учитывать.
ДАНО:
 ° °
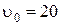 м/с
t = 2,0 с м/с
t = 2,0 с
  м/с м/с
 м м
|
 –? –?
|
АНАЛИЗ. Рассмотрим механическую систему граната – осколки. Вследствие взрыва скорость каждой части гранаты изменяется под действием сил давления газов, образующихся при взрыве. Однако если рассматривать части гранаты как систему тел, то эти силы станут внутренними. Полный импульс системы в момент взрыва меняться не будет (силы, возникающие при взрыве, настолько велики, что по сравнению с ними действием всех других сил – сопротивления воздуха, тяжести – можно пренебречь и систему можно считать замкнутой).
 Рис. 1.3.2
Рис. 1.3.2
|
РЕШЕНИЕ. Найдем координаты места взрыва и скорость гранаты в момент взрыва (рис. 1.3.2). Для этого запишем уравнение движения гранаты до взрыва:
 .
.
В момент взрыва  ,
, 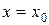 ,
,  тогда
тогда
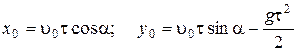 .
.
Скорость гранаты в момент взрыва  ее модуль
ее модуль 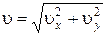 ,
,
где 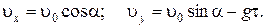
По закону сохранения импульса  . До взрыва полный импульс равен импульсу гранаты
. До взрыва полный импульс равен импульсу гранаты  где
где  – массы осколков. После взрыва импульс
– массы осколков. После взрыва импульс  равен векторной сумме импульсов осколков:
равен векторной сумме импульсов осколков: 
По условию задачи скорость меньшего осколка 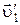 равна векторной сумме скорости гранаты
равна векторной сумме скорости гранаты  и собственной скорости
и собственной скорости 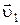 , направленной горизонтально:
, направленной горизонтально: 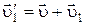 , тогда
, тогда 
Закон сохранения импульса для рассматриваемой системы можно записать в виде:  . Разделив на
. Разделив на  , имеем:
, имеем: 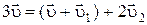 , или
, или
 . (1.3.7)
. (1.3.7)
Неизвестным является  – скорость большего осколка. Спроектируем (1.3.7) на координатные оси:
– скорость большего осколка. Спроектируем (1.3.7) на координатные оси:

Тогда скорость большего осколка равна:

Таким образом, вертикальные составляющие скоростей осколков одинаковы, 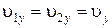 , и равны вертикальной составляющей скорости гранаты до взрыва. В этом случае уравнения движения осколков по оси Y также будут одинаковы:
, и равны вертикальной составляющей скорости гранаты до взрыва. В этом случае уравнения движения осколков по оси Y также будут одинаковы:  и время их движения одинаково.
и время их движения одинаково.
Время движения найдем из уравнения движения меньшего осколка по оси X:  . При
. При  полное время движения составит
полное время движения составит
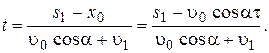
Подставив  в уравнение движения большего осколка по оси X, найдем дальность его полета
в уравнение движения большего осколка по оси X, найдем дальность его полета  :
:

Преобразовав, имеем
 ,
,
или 
Проверка размерности: [ s 2] = (м×м/с)/м/с = м. Подставив числовые значения, получаем s 2 = 19 м.
ОТВЕТ: s 2 = 19 м.
ЗАДАЧА 6. Три лодки, каждая массой  = 250 кг, идут друг за другом со скоростью
= 250 кг, идут друг за другом со скоростью  = 5,0 м/с. Из второй лодки одновременно в первую и третью бросают грузы массой по
= 5,0 м/с. Из второй лодки одновременно в первую и третью бросают грузы массой по  = 20 кг со скоростью
= 20 кг со скоростью  = 2,0 м/с относительно средней лодки. Определить скорости лодок после переброски грузов.
= 2,0 м/с относительно средней лодки. Определить скорости лодок после переброски грузов.
ДАНО:
 = 250 кг = 250 кг
 = 5,0 м/с = 5,0 м/с
 = 20 кг = 20 кг
 = 2,0 м/с = 2,0 м/с
|
 –? –?
|
АНАЛИЗ. Во взаимодействии участвуют лодки и грузы. В процессе переброски импульс груза передается лодке. Действие внешних сил в задаче не оговорено, поэтому им можно пренебречь, считать систему «лодка-груз» замкнутой и применять закон сохранения импульса.
До переброски грузов лодки движутся с постоянной скоростью. Система отсчета, связанная с лодками, является инерциальной. В этой системе отсчета начальный импульс каждой лодки равен нулю, и взаимодействие лодки и груза описывается наиболее просто.
 Рис. 1.3.3
Рис. 1.3.3
|
РЕШЕНИЕ. Систему отсчета свяжем с движущимися лодками до броска. В ней лодки неподвижны, и импульс каждой лодки равен нулю. При броске передней лодке 1 (рис.1.3.3) передается импульс  в направлении оси X, в результате чего лодка приобретает импульс
в направлении оси X, в результате чего лодка приобретает импульс  , где
, где 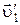 – скорость лодки в системе отсчета движущихся лодок. Таким образом:
– скорость лодки в системе отсчета движущихся лодок. Таким образом:  , или в проекции на ось X:
, или в проекции на ось X:  ,
,
отсюда 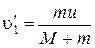 .
.
Задняя лодка 3 получает импульс  , направленный против оси X.
, направленный против оси X.
Для нее:  и
и

– лодка приобретает скорость в направлении, противоположном оси X. Из средней лодки 2 передаются импульсы  и
и  , поэтому суммарный импульс, передаваемый лодкой, равен нулю:
, поэтому суммарный импульс, передаваемый лодкой, равен нулю:  и
и  .
.
Скорости лодок после переброски в системе отсчета, связанной с Землей, равны:
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
Правильность формулы по размерности очевидна. Подставив значения, получаем  м/с;
м/с;  м/с;
м/с;  м/с.
м/с.
ОТВЕТ:  м/с;
м/с;  м/с;
м/с;  м/с.
м/с.
ЗАДАЧА 7. Модель ракеты движется при отсутствии внешних сил, выбрасывая непрерывно струю газов с постоянной относительно нее скоростью  м/с (рис. 1.3.4). Расход газа m = 0,4 кг/с, начальная масса ракеты
м/с (рис. 1.3.4). Расход газа m = 0,4 кг/с, начальная масса ракеты 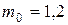 кг. Какую скорость относительно Земли приобретает ракета через время
кг. Какую скорость относительно Земли приобретает ракета через время  = 1 с после начала движения, если начальная скорость равна нулю? Оценить погрешность, сделанную при пренебрежении силой тяжести.
= 1 с после начала движения, если начальная скорость равна нулю? Оценить погрешность, сделанную при пренебрежении силой тяжести.
ДАНО:
 м/с
m = 0,4 кг/с м/с
m = 0,4 кг/с
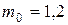 кг кг
 = 1 с = 1 с
|
 –? –?
|
АНАЛИЗ. Ракета переменной массы и газ, выбрасываемый из ракеты с заданной постоянной относительной скоростью, совершают поступательное движение. Система замкнутая, следовательно, ее импульс остается постоянным
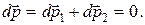 (1.3.8)
(1.3.8)
Импульсы каждого из тел изменяются непрерывно со временем, поэтому необходимо найти изменение импульса 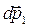 ракеты за некоторый промежуток времени dt и изменение импульса
ракеты за некоторый промежуток времени dt и изменение импульса  той порции газа, которая за этот промежуток времени истекает из ракеты.
той порции газа, которая за этот промежуток времени истекает из ракеты.
 Рис. 1.3.4
Рис. 1.3.4
|
Если в момент времени  ракета обладала скоростью
ракета обладала скоростью  и массой
и массой  , то за интервал времени
, то за интервал времени  скорость ракеты за счет реактивного движения выбрасываемой струи газа изменяется на
скорость ракеты за счет реактивного движения выбрасываемой струи газа изменяется на  , а импульс – на величину
, а импульс – на величину
 . (1.3.9)
. (1.3.9)
Порция газа  , двигаясь вместе с ракетой, обладала скоростью
, двигаясь вместе с ракетой, обладала скоростью  относительно Земли. В результате выброса со скоростью
относительно Земли. В результате выброса со скоростью  относительно ракеты эта порция приобрела скорость
относительно ракеты эта порция приобрела скорость  относительно Земли. Изменение импульса
относительно Земли. Изменение импульса  порции газа за время
порции газа за время  составляет
составляет
 . (1.3.10)
. (1.3.10)
Решая совместно эти уравнения, находим закон изменения скорости.
РЕШЕНИЕ. Подставив (1.3.9) и (1.3.10) в выражение (1.3.8), получим
 или
или  . (1.3.11)
. (1.3.11)
Если начальная скорость ракеты равна нулю, то ее движение будет прямолинейным. Направим ось X параллельно вектору скорости ракеты  (рис.1.3.5). Тогда
(рис.1.3.5). Тогда 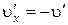 . Перепишем уравнение (1.3.11) в скалярной форме:
. Перепишем уравнение (1.3.11) в скалярной форме:
 .
.
Разделим обе части равенства на  :
:
 .
.
Проинтегрируем полученное выражение в пределах от нуля до  , учитывая начальные условия: при
, учитывая начальные условия: при  ,
, 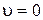 :
:

Проверка размерности не требуется. Подставив значения, получим  м/с.
м/с.
Рассмотрим теперь влияние силы тяжести на движение системы. По отношению к системе эта сила является внешней. Следовательно, замкнутость системы нарушается, поэтому уравнения (1.3.8) и (1.3.11) примут вид:


В нашем случае  , следовательно,
, следовательно,
 (1.3.12)
(1.3.12)
Для оценки максимальной погрешности следует взять наибольшее значение силы тяжести  (в момент старта ракеты) и предположить, что ракета движется вертикально вверх, а вектор
(в момент старта ракеты) и предположить, что ракета движется вертикально вверх, а вектор  направлен вниз коллинеарно с вектором
направлен вниз коллинеарно с вектором  . Тогда уравнение (1.3.12) в скалярной форме примет вид:
. Тогда уравнение (1.3.12) в скалярной форме примет вид:
 . (1.3.13)
. (1.3.13)
Из сравнения выражений (1.3.11) и (1.3.13) видно, что, не учитывая силы тяжести, мы пренебрегаем членом  по сравнению с единицей.
по сравнению с единицей.
Для данной задачи  » 0,037.
» 0,037.
Можно показать, что пренебрежение силой тяжести в окончательном выражении для скорости дает ту же относительную погрешность. Действительно, обозначим в уравнении (1.3.12) через С выражение, стоящее в скобках:
 .
.
Тогда получаем:  . Разделив на
. Разделив на  , имеем:
, имеем:  . После интегрирования получаем:
. После интегрирования получаем:  .
.
Относительная погрешность при определении скорости
 , т. е. 3,7 %.
, т. е. 3,7 %.
ОТВЕТ: 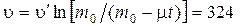 м/с.
м/с.
ЗАДАЧА 8. Водометный двигатель катера забирает воду из реки и выбрасывает ее со скоростью  = 10,0 м/с относительно катера назад. Масса катера
= 10,0 м/с относительно катера назад. Масса катера  = 1000 кг. Масса ежесекундно выбрасываемой воды постоянна и равна
= 1000 кг. Масса ежесекундно выбрасываемой воды постоянна и равна  =10,0 кг/с. Пренебрегая сопротивлением воды движению катера, определить: а) скорость катера
=10,0 кг/с. Пренебрегая сопротивлением воды движению катера, определить: а) скорость катера  спустя время
спустя время  = 1,00 мин после начала движения; б) какой предельной скорости
= 1,00 мин после начала движения; б) какой предельной скорости 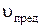 может достичь катер.
может достичь катер.
ДАНО:
 = 10,0 м/с; = 10,0 м/с;  = 1000 кг = 1000 кг
 = 10,0 кг/с; = 10,0 кг/с;  = 60,0 с = 60,0 с
|
 –? –?  –? –?
|
АНАЛИЗ. Во взаимодействии участвуют два тела – катер и вода, которые образуют замкнутую систему. За время  струя воды уносит импульс
струя воды уносит импульс  где
где  – масса воды,
– масса воды,
 Рис. 1.3.5
Рис. 1.3.5
|
 – скорость струи воды относительно Земли. Изменение импульса катера в результате выброса воды
– скорость струи воды относительно Земли. Изменение импульса катера в результате выброса воды  , где
, где  – скорость, приобретенная катером за время
– скорость, приобретенная катером за время  . Согласно закону сохранения импульса суммарный импульс системы остается неизменным и равен нулю:
. Согласно закону сохранения импульса суммарный импульс системы остается неизменным и равен нулю: 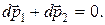 Решая это уравнение с учетом начальных условий, находим скорость катера.
Решая это уравнение с учетом начальных условий, находим скорость катера.
РЕШЕНИЕ. Оба импульса направлены по одной прямой противоположно (рис.1.3.5), поэтому закон сохранения импульса в скалярной форме можно записать в виде
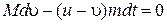 или
или 
Проинтегрировав, получаем  (1.3.14)
(1.3.14)
Подставим начальные условия: в момент времени  = 0 скорость катера равна нулю,
= 0 скорость катера равна нулю,  = 0, тогда
= 0, тогда 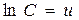 . Подставив
. Подставив 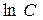 в выражение (1.3.14), имеем
в выражение (1.3.14), имеем  . Потенцируя, получаем
. Потенцируя, получаем  или
или  .
.
Окончательно закон изменения скорости катера со временем имеет вид:  . (1.3.14а)
. (1.3.14а)
Правильность формулы по размерности очевидна. Спустя время  мин скорость катера равна
мин скорость катера равна
 м/с.
м/с.
Для определения предельной скорости катера перейдем к пределу в выражении (1.3.14а) при t ® ¥:

Ясно, что  , поэтому
, поэтому  м/с.
м/с.
ОТВЕТ:  м/с;
м/с;  м/с.
м/с.
ЗАДАЧА 9. Акробат массой М = 50 кг, имея при себе груз  = 5 кг, прыгает под углом a = 60° к горизонту со скоростью
= 5 кг, прыгает под углом a = 60° к горизонту со скоростью 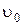 = 6 м/с. В наивысшей точке своей траектории он бросает груз горизонтально назад с относительной скоростью
= 6 м/с. В наивысшей точке своей траектории он бросает груз горизонтально назад с относительной скоростью  = 2 м/с. На сколько увеличилась дальность прыжка вследствие этого?
= 2 м/с. На сколько увеличилась дальность прыжка вследствие этого?
ДАНО:
 кг кг
 кг
a = 60° кг
a = 60°
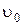 = 6 м/с = 6 м/с
 = 2 м/с = 2 м/с
|
| D s –? |
АНАЛИЗ. Во взаимодействии участвуют два тела – акробат и груз, которые движутся в поле силы тяжести, поэтому систему тел в любой момент времени нельзя считать замкнутой. Время броска мало в сравнении с временем движения тел, поэтому изменением импульса системы за время броска можно пренебречь и считать систему тел замкнутой. Таким образом, импульс системы до и после броска остается постоянным.
Чтобы найти увеличение дальности полета акробата, вычислим увеличение его скорости. Запишем закон сохранения импульса в системе отсчета, связанной с акробатом в момент броска. В этой системе отсчета до броска акробат неподвижен. Приобретенная им после броска скорость равна увеличению его скорости относительно Земли.
 Рис. 1.3.6
Рис. 1.3.6
|
РЕШЕНИЕ. В системе отсчета, связанной с Землей, скорость акробата по оси  постоянна и равна
постоянна и равна  . Выберем вспомогательную систему отсчета
. Выберем вспомогательную систему отсчета  (рис. 1.3.6), которая движется относительно Земли со скоростью
(рис. 1.3.6), которая движется относительно Земли со скоростью  по оси
по оси  (ясно, что эта система является инерциальной). В системе
(ясно, что эта система является инерциальной). В системе  до броска акробат движется только вдоль вертикальной оси
до броска акробат движется только вдоль вертикальной оси  .
.
В результате броска акробат приобрел импульс 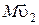 , направленный по оси
, направленный по оси  , а груз – импульс
, а груз – импульс 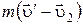 , направленный против оси
, направленный против оси  .
.
По закону сохранения импульса  , отсюда
, отсюда  .
.
Следует заметить, что  – это относительная скорость груза (т. е. скорость груза относительно акробата). Скорость груза в системе отсчета
– это относительная скорость груза (т. е. скорость груза относительно акробата). Скорость груза в системе отсчета  равна
равна  . За счет приобретенного импульса акробат увеличивает дальность полета на
. За счет приобретенного импульса акробат увеличивает дальность полета на  , где
, где  – время движения от верхней точки до Земли. Очевидно, верхняя точка траектории поднята над землей на высоту
– время движения от верхней точки до Земли. Очевидно, верхняя точка траектории поднята над землей на высоту 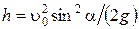 .
.
Уравнение движения акробата по оси Y ¢ после броска имеет вид:  В момент падения на землю
В момент падения на землю  и время движения после броска равно
и время движения после броска равно  тогда
тогда 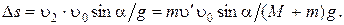
Проверим размерность:  . Подставив значения, получаем Ds = 5 × 2 × 6sin60°/((50 + 5) × 9,8) = 0,096 м.
. Подставив значения, получаем Ds = 5 × 2 × 6sin60°/((50 + 5) × 9,8) = 0,096 м.
ОТВЕТ:  м.
м.
ЗАДАЧА 10. Тело массой m начинает двигаться под действием силы  . Найти мощность
. Найти мощность  , развиваемую силой, в момент времени
, развиваемую силой, в момент времени  .
.
ДАНО:
т (кг)
 , Н , Н
 (с) (с)
|
| Р (t) –? |
АНАЛИЗ. Для определения мощности, развиваемой силой, необходимо, кроме вектора силы, знать вектор скорости тела. Для этого из второго закона Ньютона следует выразить ускорение как функцию времени и проинтегрировать эту функцию. Мощность равна скалярному произведению силы и скорости 
РЕШЕНИЕ. Ускорение тела найдем по второму закону Ньютона:
 а скорость из соотношения:
а скорость из соотношения: 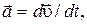 откуда
откуда  и
и  Тогда мощность
Тогда мощность
 или
или  , (константа интегрирования равна нулю, т. к. при t = 0 скорость равна нулю).
, (константа интегрирования равна нулю, т. к. при t = 0 скорость равна нулю).
Правильность формулы по размерности очевидна.
ОТВЕТ:  .
.
ЗАДАЧА 11. Первоначально покоившаяся частица, находясь под действием силы  (Н) переместилась из точки с координатами (2,4,6) в точку (3,6,9) (м). Найти кинетическую энергию частицы в конечной точке.
(Н) переместилась из точки с координатами (2,4,6) в точку (3,6,9) (м). Найти кинетическую энергию частицы в конечной точке.
ДАНО:
 (Н)
А (2, 4, 6), м
В (3,6,9), м (Н)
А (2, 4, 6), м
В (3,6,9), м
|
| Т –? |
АНАЛИЗ. В задаче рассматривается частица, начальная скорость которой равна нулю. Под действием постоянной силы эта частица перемещается из положения с радиус-вектором  в положение с радиус-вектором
в положение с радиус-вектором  . Работа силы идет на приращение кинетической энергии частицы. Это приращение равно кинетической энергии в конечной точке.
. Работа силы идет на приращение кинетической энергии частицы. Это приращение равно кинетической энергии в конечной точке.
РЕШЕНИЕ. Кинетическая энергия частицы увеличивается за счет действия на нее силы  и равна работе этой силы:
и равна работе этой силы:  где
где  – перемещение частицы,
– перемещение частицы,  Тогда
Тогда  .
.
Проверка размерности: [ Т ] = Н×м = Дж. Подставив значения, получаем 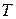 =14 Дж.
=14 Дж.
ОТВЕТ: Т = 14 Дж.
ЗАДАЧА 12. Потенциальная энергия частицы имеет вид:  , где
, где  . Найти: а) силу, действующую на частицу; б) работу А, совершаемую над частицей силами поля при переходе частицы из точки (1,1,1) в точку (2,2,3).
. Найти: а) силу, действующую на частицу; б) работу А, совершаемую над частицей силами поля при переходе частицы из точки (1,1,1) в точку (2,2,3).
ДАНО:
 , Дж , Дж
 , Дж
А (1,1,1)
В (2,2,3) , Дж
А (1,1,1)
В (2,2,3)
|
| F –? A –? |
АНАЛИЗ. В задаче требуется найти силу, действующую на частицу, по заданной функции потенциальной энергии. Для этого следует воспользоваться соотношением между силой и потенциальной энергией. Работа силы равна убыли потенциальной энергии. Зная координаты начального и конечного положения частицы, эту убыль легко найти.
РЕШЕНИЕ. Сила и потенциальная энергия частицы связаны соотношением

Подставив функцию, получаем: 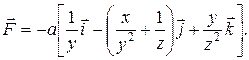
Проверим размерность: [  ] = Дж/м = Н.
] = Дж/м = Н.
Работа над частицей совершается силами потенциального поля и равна убыли потенциальной энергии частицы:  ,
,
где  – потенциальная энергия в точке (1,1,1),
– потенциальная энергия в точке (1,1,1), 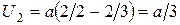 – потенциальная энергия в точке (2,2,3). Тогда
– потенциальная энергия в точке (2,2,3). Тогда

ОТВЕТ:  ;
; 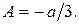
ЗАДАЧА 13. Невесомая нерастяжимая нить может скользить без трения по изогнутому желобу (рис. 1.3.7). К концам нити прикреплены грузы массами  кг и
кг и  = 1 кг. Груз массой m 1 поднимают настолько, чтобы груз массой m 2 коснулся пола и отпускают. Высота
= 1 кг. Груз массой m 1 поднимают настолько, чтобы груз массой m 2 коснулся пола и отпускают. Высота  = 1,0 м. На какую высоту
= 1,0 м. На какую высоту  над полом поднимется груз массой m 2 после того, как груз массой m 1 ударится об пол?
над полом поднимется груз массой m 2 после того, как груз массой m 1 ударится об пол?
ДАНО:
 = 3 кг = 3 кг
 = 1 кг = 1 кг
 = 1,0 м = 1,0 м
|
| h 2 –? |
АНАЛИЗ. Система грузов находится в потенциальном поле – поле тяжести Земли, поэтому полная механическая энергия системы сохраняется. В начальный момент времени тело  обладало потенциальной энергией
обладало потенциальной энергией  . Далее система была предоставлена себе, и потенциальная энергия первого тела перешла в кинетическую энергию этого тела
. Далее система была предоставлена себе, и потенциальная энергия первого тела перешла в кинетическую энергию этого тела  и потенциальную энергию второго тела.
и потенциальную энергию второго тела.
Записав закон сохранения энергии для системы тел, получаем уравнение с двумя неизвестными:  (высота, на которую поднялось второе тело) и
(высота, на которую поднялось второе тело) и  (скорость первого тела). Рассмотрев равноускоренное движение первого тела с высоты
(скорость первого тела). Рассмотрев равноускоренное движение первого тела с высоты  до пола, найдем время движения и приобретенную им скорость
до пола, найдем время движения и приобретенную им скорость  . Ускорение системы тел найдем из уравнения динамики.
. Ускорение системы тел найдем из уравнения динамики.
 Рис. 1.3.7
Рис. 1.3.7
|
РЕШЕНИЕ. Согласно закону сохранения энергии
 (1.3.15)
(1.3.15)
Первое тело опускалось в течение времени  с высоты
с высоты  , причем
, причем  , отсюда
, отсюда  , где
, где  – ускорение системы:
– ускорение системы:

(см. раздел 1.1.2). За время  первое тело приобрело скорость
первое тело приобрело скорость 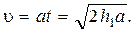 Тогда из (1.3.15) получаем:
Тогда из (1.3.15) получаем:  .
.
Подставив  , имеем:
, имеем:  .
.
Разделив на  и сгруппировав, получим:
и сгруппировав, получим:
 или
или

Тогда  и
и  .
.
Правильность формулы по размерности очевидна. Подставив значения, имеем h 2 = 1,5 м.
ОТВЕТ: h 2 = 1,5 м.
ЗАДАЧА 14. В системе, показанной на рис. 1.3.8, масса каждого бруска  кг, жесткость пружины
кг, жесткость пружины 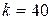 Н/м, коэффициент трения между бруском и плоскостью m = 0,20. Массы блока и пружины пренебрежительно малы. Система пришла в движение с нулевой начальной скоростью при недеформированной пружине. Найти максимальную скорость брусков.
Н/м, коэффициент трения между бруском и плоскостью m = 0,20. Массы блока и пружины пренебрежительно малы. Система пришла в движение с нулевой начальной скоростью при недеформированной пружине. Найти максимальную скорость брусков.
ДАНО:
 = 0,50 кг = 0,50 кг
 = 40 Н/м
m = 0,20 = 40 Н/м
m = 0,20
|
 –? –?
|
АНАЛИЗ. Система находится в поле консервативных сил упругости (со стороны пружины) и тяжести. Поэтому полная энергия системы сохраняется. Рассмотрим произвольный момент времени движения системы. Первое тело опустилось на высоту  , его потенциальная энергия при этом уменьшилась на
, его потенциальная энергия при этом уменьшилась на  . Пружина растянулась на
. Пружина растянулась на  , ее потенциальная энергия увеличилась на
, ее потенциальная энергия увеличилась на  . Движущиеся тела совершили работу против силы трения
. Движущиеся тела совершили работу против силы трения  . Нить, соединяющая тела, нерастяжимая, поэтому скорости обоих тел одинаковы, и суммарная кинетическая энергия системы равна
. Нить, соединяющая тела, нерастяжимая, поэтому скорости обоих тел одинаковы, и суммарная кинетическая энергия системы равна  . В начальный момент времени полная энергия системы равна нулю.
. В начальный момент времени полная энергия системы равна нулю.
Для определения скорости движения брусков запишем закон сохранения энергии для рассматриваемой системы тел. Эта скорость является функцией величины деформации пружины  . Поэтому для определения максимальной скорости необходимо взять производную от
. Поэтому для определения максимальной скорости необходимо взять производную от  по
по  и приравнять ее к нулю.
и приравнять ее к нулю.
 Рис. 1.3.8
Рис. 1.3.8
|
РЕШЕНИЕ. Согласно закону сохранения энергии имеем:

или  . Отсюда
. Отсюда  и скорость движения системы
и скорость движения системы
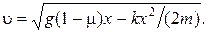 (1.3.16)
(1.3.16)
Чтобы найти максимальную скорость брусков, продифференцируем выражение (1.3.16) по  и приравняем производную к нулю:
и приравняем производную к нулю:
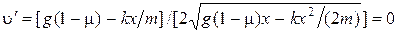 .
.
Имеем: 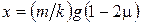 . Тогда максимальная скорость
. Тогда максимальная скорость


Проверим размерность:
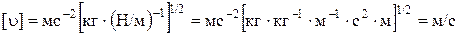 . Подставив значения, получаем:
. Подставив значения, получаем:  (м/с).
(м/с).
ОТВЕТ:  м/с.
м/с.
ЗАДАЧА 15. С вершины идеально гладкой сферы соскальзывает небольшой груз. С какой высоты  , считая от вершины, груз сорвется со сферы? Радиус сферы
, считая от вершины, груз сорвется со сферы? Радиус сферы  = 90 см (рис. 1.3.9).
= 90 см (рис. 1.3.9).
ДАНО:
 = 0,9 м = 0,9 м
|
| h –? |
 Рис. 1.3.9
Рис. 1.3.9
|
АНАЛИЗ. Груз, который можно считать точечным, до некоторой точки – точки отрыва от сферы – движется по дуге окружности радиуса  .
.
На груз во время его движения по сфере действует сила тяжести  и сила нормальной реакции
и сила нормальной реакции  со стороны сферы. Согласно второму закону Ньютона, имеем:
со стороны сферы. Согласно второму закону Ньютона, имеем:
 . (1.3.17)
. (1.3.17)
Проекции этих сил на направление, нормальное к траектории, сообщают телу нормальное ускорение  , где
, где  – мгновенная скорость тела. В точке отрыва С прекращается взаимодействие между движущимся телом и поверхностью сферы, следовательно, сила давления тела на сферу и, соответственно, сила нормальной реакции
– мгновенная скорость тела. В точке отрыва С прекращается взаимодействие между движущимся телом и поверхностью сферы, следовательно, сила давления тела на сферу и, соответственно, сила нормальной реакции  обращаются в ноль. Таким образом, в этой точке нормальное ускорение сообщает телу только проекция силы тяжести.
обращаются в ноль. Таким образом, в этой точке нормальное ускорение сообщает телу только проекция силы тяжести.
Для того чтобы определить высоту, на которой находится точка отрыва, надо найти связь скорости тела при его движении по сфере с его координатами (с высотой). Такую связь можно найти, зная законы изменения со временем координат и скорости тела при движении тела в поле силы тяжести Земли. Поскольку сила нормальной реакции работы не совершает, полная энергия тела остается постоянной:
 . (1.3.18)
. (1.3.18)
Очевидно, применение закона сохранения энергии к переходу из начального состояния в точку отрыва дает в явном виде связь между скоростью тела и высотой рассматриваемой точки.
РЕШЕНИЕ. За начало отсчета потенциальной энергии тела примем точку отрыва. Тогда на вершине сферы тело обладает потенциальной энергией  , а изменение потенциальной энергии при скольжении тела от вершины до точки отрыва равно
, а изменение потенциальной энергии при скольжении тела от вершины до точки отрыва равно
 . (1.3.19)
. (1.3.19)
Здесь  – искомая высота, отсчитываемая от вершины сферы. Изменение кинетической энергии при движении груза
– искомая высота, отсчитываемая от вершины сферы. Изменение кинетической энергии при движении груза
 . (1.3.20)
. (1.3.20)
На вершине сферы тело находится в положении неустойчивого равновесия, и  . Подставляя (1.3.19) и (1.3.20) в выражение (1.3.18), получаем:
. Подставляя (1.3.19) и (1.3.20) в выражение (1.3.18), получаем:
 (1.3.21)
(1.3.21)
В векторном уравнении (1.3.17) перейдем к скалярной форме, спроектировав это уравнение на координатную ось X (рис. 1.3.9). Ясно, что  , тогда из (1.3.17) получаем
, тогда из (1.3.17) получаем 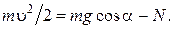
В точке отрыва от сферы  и
и  .
.
Из рис. 1.3.9 видно, что  . Тогда
. Тогда
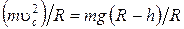 . (1.3.22)
. (1.3.22)
Решая совместно уравнения (1.3.21) и (1.3.22), имеем 
тогда  и
и  = 0,30 м.
= 0,30 м.
Правильность формулы по размерности очевидна.
ОТВЕТ: h = 0,30 м.
ЗАДАЧА 16. По теории Резерфорда-Бора электрон в атоме может двигаться по плоским эллиптическим орбитам. Какова полная энергия электрона в атоме водорода, если большая полуось эллипса a = 2,1×10–8 см, а ядро находится в одном из фокусов эллипса (рис. 1.3.10). Сила притяжения электрона к ядру  , где r – расстояние от ядра до точки, в которой находится электрон; B = 2,3×10-28 Н×м2.
, где r – расстояние от ядра до точки, в которой находится электрон; B = 2,3×10-28 Н×м2.
| ДАНО: a = 2,1×10–10 м F = B / r 2 (Н) B = 2,3×10–28 Н×м2 |
| Е –? |
АНАЛИЗ. Во время движения электрона при любом его положении на него действует только сила притяжения со стороны ядра. Эта сила зависит от расстояния r (т. е. координаты точки, в которой находится электрон) и направлена к ядру. Следовательно, можно говорить, что электрон движется в силовом поле, консервативном и центральном, центр которого совпадает с положением ядра.
 Рис. 1.3.10
Рис. 1.3.10
|
При движении в таком поле электрон обладает потенциальной энергией, полная его энергия и момент импульса остаются постоянными. Чтобы найти полную энергию электрона, необходимо записать в явном виде законы сохранения энергии и момента импульса для двух произвольных фиксированных положений электрона на орбите.
Изменение потенциальной энергии определяется работой сил поля, взятой с обратным знаком  , где
, где  – проекция силы на направление радиуса-вектора
– проекция силы на направление радиуса-вектора  .
.
Если выбрать начало отсчета потенциальной энергии в некоторой точке






