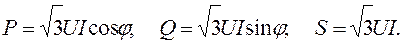Совокупность трех ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе относительно друг друга на треть периода, называется трехфазной системой ЭДС.
Выражения для мгновенных значений ЭДС симметричного трехфазного источника имеют следующий вид:
.
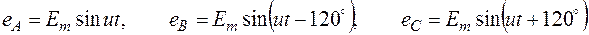В комплексной форме ЭДС записываются в виде
Электрическая цепь, в которой действует трехфазная система ЭДС, называется трехфазной цепью.
Термин «фаза» в электротехнике имеет два значения: с одной стороны — это аргумент синусоидальной функции времени, с другой — часть многофазной цепи, по которой протекает один и тот же ток.
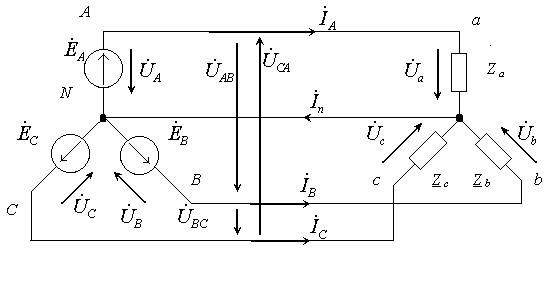
На рис. 1 показана схема трехфазной цепи, в которой фазы источника и приемника соединены звездой.Зажимы А, В, С источника и зажимы a, b, c приемника называют линейными зажимами. Провода, соединяющие линейные зажимы источника и приемника, называются линейными проводами. Точки N и n называются нейтральными точками источника и приемника, а провод, соединяющий эти точки, — нейтральным.
 |
|
|
|
Фазные напряжения источника равны соответствующим ЭДС.
При наличии нейтрального провода трехфазная цепь называется четырехпроводной (рис. 1). В четырехпроводной цепи, при пренебрежении сопротивлениями линейных и нейтрального проводов, линейные и фазные напряжения приемника равны соответствующим напряжениям источника и остаются неизменными независимо от величины и характера сопротивлений фаз приемника (Uab = UAB; Ubc = UBC; Uca = UCA; Ua = UA; Ub = UB ; Uc = UC).
Принятые положительные направления ЭДС, линейных и фазных напряжений и токов показаны на рис. 1.
Комплексные значения линейных напряжений равны разности комплексных значений соответствующих фазных напряжений. Для линейных напряжений приемника можно записать
Из векторной диаграммы (рис. 2) видно, что в этом случае действующее значение линейного напряжения 
.
Токи в фазах источника и приемника называются фазными, токи в линейных проводах — линейными. Как видно из рис. 1, при соединении звездой фазный ток является одновременно линейным: IФ = Iл.
При наличии нейтрального провода комплексные значения токов определяются из выражений
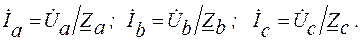
В соответствии с первым законом Кирхгофа ток в нейтральном проводе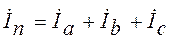 
.
|
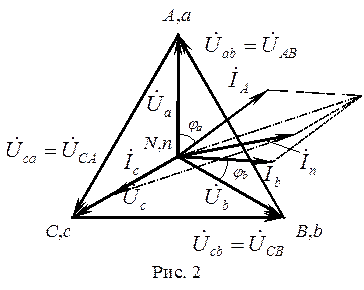
На рис. 2 показана векторная диаграмма для четырехпроводной цепи при несимметричном приемнике: в фазе а нагрузка – активно-индуктивная (jа > 0), в фазе b – активно-емкостная (jb < 0), в фазе с – активная (jс = 0).
Вектор тока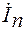 
в нейтральном проводе определен путем суммирования векторов линейных токов.
При симметричном приемнике (Z a= Z b= Z c) сумма комплексных значений линейных токов равна нулю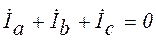 
, и необходимость в нейтральном проводе отпадает.
|
На рис. 3 показана векторная диаграмма для четырехпроводной цепи при симметричном режиме для активного характера нагрузки (j = 0).
При отсутствии нейтрального провода (трехпроводная цепь) напряжение на фазах приемника зависит от величины и характера сопротивлений фаз. Поэтому соединение звездой без нейтрального провода применяется только для симметричных приемников.
Напряжение 
между нейтральными точками приемника и источника (напряжение смещения нейтрали) определяется по формуле узлового напряжения (по методу двух узлов)
,
где 
– комплексные проводимости фаз.
Комплексные значения токов
|
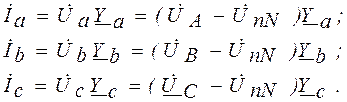
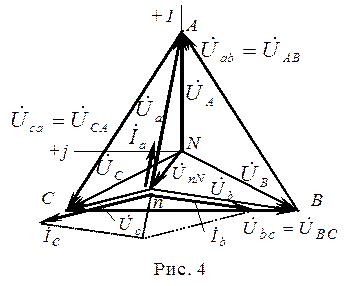
На рис. 4 показана векторная диаграмма напряжений и токов при активной неравномерной нагрузке (Ra > Rb > Rc).
Построение векторной диаграммы для трехпроводной цепи по экспериментальным данным целесообразно проводить в следующем порядке:
– в выбранном масштабе построить векторную диаграмму напряжений источника 
; – засечками, по измеренным фазным напряжениям приемника Ua, Ub, Uc, из точек А, В, С соответственно, определить положение нейтральной точки n приемника;
– построить вектор напряжения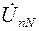 
смещения нейтрали, соединив нейтральные точки источника N и приемника n;
– соединить нейтраль приемника n с вершинами треугольника линейных напряжений А, В, С (эти отрезки образуют векторы соответствующих фазных напряжений приемника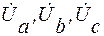 
);
– построить в выбранном масштабе векторы токов, совместив их начала с нейтралью приемника n (ориентация векторов токов относительно соответствующих векторов фазных напряжений приемника определяется характером нагрузки фаз приемника).
Правильность построения векторной диаграммы следует проверить по первому закону Кирхгофа: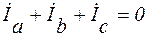 
.
Мощности в трехфазных цепях определятся как алгебраические суммы мощностей отдельных фаз:
– активная мощность P = Pa+ Pb+ Pc ;
– реактивная мощность Q = Qa+ Qb+ Qc,
где мощности отдельной фазы: 
;
.
Полная мощность трехфазной цепи 
.
При симметричной нагрузке
