● Уравнение гармонических колебаний
х = А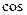 
(ω0 t + φ0),
где s – смещение колеблющейся величины от положения равновесия; Α – амплитуда колебаний; ω0 = 2 π / T = 2 πν – круговая (циклическая) частота;
ν = 1/ T – частота; T – период колебаний; (ω0t+φ0) – фаза колебаний; φ 0 – начальная фаза.
● Скорость и ускорение точки, совершающей гармонические колебания,
;
.
● Кинетическая энергия колеблющейся точки массой m
● Потенциальная энергия
● Полная энергия
.
● Дифференциальное уравнение гармонических колебаний материальной
точки массой m
, или 
,
где k – коэффициент упругости (k = ω02m).
● Период колебаний пружинного маятника
,
где m – масса пружинного маятника; k - жесткость пружины.
● Период колебаний физического маятника
,
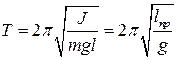где Ј – момент инерции маятника относительно оси колебаний;
l – расстояние между точкой подвеса и центром масс маятника;
– приведенная длина физического маятника; g – ускорение свободного падения.
● Период колебаний математического маятника
,
где l – длина маятника.
● Формула Томсона, устанавливающая связь между периодом Т собсвен-
ных колебаний в контуре без активного сопротивления и индуктивностью L и емкостью контура С,
Т = 2 π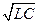 
.
● Дифференциальное уравнение свободных гармонических колебаний
заряда в контуре и его решение:
; 
,
где 
- амплитуда колебаний заряда; 
- собственная частота контура.
● Дифференциальное уравнение свободных затухающих колебаний
линейной системы и его решение:
; 
,
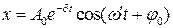где х – колеблющаяся величина, описывающая физический процесс;
δ – коэффициент затухания (
в случае механических колебаний и
в случае электромагнитных колебаний); ω0 – циклическая частота свободных незатухающих колебаний той же колебательной системы;
- частота затухающих колебаний; 
– амплитуда затухающих колебаний.
● Декремент затухания
,
где А(t) и A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период.
● Логарифмический декремент затухания
,
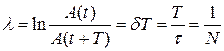где τ = 1/ δ – время релаксации; N – число колебаний, совершаемых за время уменьшения амплитуды в е раз.
● Добротность колебательной системы
.
● Дифференциальное уравнение вынужденных колебаний и его решение
для установившихся колебаний:
, 
,
где х– колеблющаяся величина, описывающая физический процесс
(
в случае механических колебаний,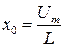 
в случае электромагнитных колебаний);
; 
.
● Резонансная частота и резонансная амплитуда
; 
.
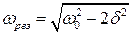● Сдвиг фаз между напряжением и силой тока
.
