Погрешности измерений. Тема 3. Погрешности измерений и средств измерений

Тема 3. Погрешности измерений и средств измерений

Погрешности измерений

Отклонение результата измере­ния от истинного значения измеряемой величины называется погреш­ностью измерения. Различают абсолютные погрешности измерения, ко­торые выражаются в единицах измеряемой величины, и относительные погрешности измерения, определяемые как отношение абсолютной по­грешности измерения к значению измеряемой величины:

Δ = х – х_и; (3.1)

δ = Δ/х, (3.2)

 

где Δ - абсолютная погрешность измерения; х - значение, полученное при измерении; х_и - истинное значение измеряемой величины; δ - относительная погрешность измерения.

Абсолютная погрешность Δ является резуль­тирующей погрешностью, т.е. суммой систематической Δ_с и случайной Δ₀ погрешностей.

Систематической погрешностью измерения называется составляющая погрешности измерения, остающаяся постоянной или закономерно изме­няющаяся при повторных измерениях одной и той же величины (неисправности измерительной аппаратуры, несовершенство метода измерений, неправильная установка измерительных приборов и т.д.).

Случайной погрешностью измерения называется составляющая по­грешности измерения, изменяющаяся случайным образом при повтор­ных измерениях одной и той же величины. Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельно­сти мало влияет на результат измерения.

Результат измерения, содержащий грубую погрешность (промах), следует выявить, исключить и не учитывать при дальнейшей статисти­ческой обработке.

Существуют некото­рые общие причины возникновения систематических погрешностей, в соответствии с которыми их подразделяют на методические, инструмен­тальные и субъективные.

Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вслед­ствие внесения термопары).

Инструментальные погрешности зависят от погрешностей применяе­мых средств измерения. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуа­тации и т.д. являются причинами инструментальных погрешностей.

Субъективные погрешности вызываются неправильными отсчетами показаний прибора оператором.

Систематические погрешности могут оставаться постоянными либо закономерно изменяться. В последнем случае их подразделяют на про­грессирующие (возрастающие или убывающие), периодические и из­меняющиеся по сложному закону. Обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению или исключению посредством введения поправки.

Поправкой называется значение величины, одноименной с измеряе­мой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности.

В некоторых случаях используют поправочный множитель - число, на которое умножают результат измерения для исключения системати­ческой погрешности.

Согласно теория вероятностей слу­чайная величина наиболее полно характеризуется своим законом рас­пределения (или плотностью распределения) вероятностей. При измерении чаще всего встречается нормальная и равномерная плотность распределения случайной величины.

Рисунок 3.1 – Нормальный закон распределения погрешностей

Нормальный закон распределения вероятностей имеет вид

(3.3)

где - плотность вероятностей случайной погрешности 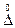; σ -среднее квадратическое значение случайной погрешности.

Кривые, соответствующие выражению (3.3) для разных значений σ, приведены на (рис.3.1). Очевидно, что при малых значениях σ получается погрешность измерений меньше, чем при больших.

Вероятность того, что погрешность результата измерения находится между заданными предельными значениям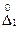и и 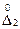вычисляется по формуле:

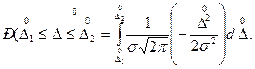(3.4)

Интеграл в формуле (3.4) вычисляется по таблицам функции Лапласа Ф(z).

Распределение погрешностей принимают равномерным, если

(3.5)

Такой закон распределения характерен, например, для погрешностей отсчета по шкале прибора, погрешностей дискретности в цифровых измерительных приборах, погрешностей квантования в аналого-цифро­вых преобразователях (АЦП).

Поскольку истинное значение измеряемой величины х_и неизвестно, непосредственно случайную абсолютную погрешность Δ вычислить нельзя. При практических расчетах приходится вместо х_и использовать его оцен­ку. Обычно принимают, что истинное значение равно среднему арифме­тическому значению ряда измерений:

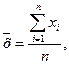
где x_i - результаты отдельных измерений; n - число измерений.

Введем важные понятия доверительной вероятности и доверитель­ного интервала. Среднее арифметическое зна­чение , полученное в результате некоторого ряда измерений, является оценкой истинного значения х_и и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Р_д есть вероятность того, что 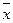отличается от х_и не более чем на Δ, т.е.

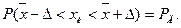(3.6)

Вероятность Р_д называется доверительной вероятностью, а интервал значений измеряемой величины от х – Δ до х + Δ - доверительным интервалом.

Приведенное выше равенство означает, что с вероятностью Р_д доверительный интервал от х - Δ до х + Δ заключает в себе истинное значение х_и.

Таким образом, чтобы характеризовать случайную погреш­ность достаточно полно, надо располагать двумя числами - доверитель­ной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал.