Количество разработанных к настоящему времени ДЭМП невелико по сравнению с НЭМП, но именно они реально могут быть использованы для расчетов надежности вычислительных систем [6.5]. Причиной этого является прежде всего аргумент ДЭМП - порядковый номер испытаний, а не время, условное или фактическое при любых способах его измерения или учета. Как указано в [6.3], «…хотя желание выразить надежность ПО некоторой функцией времени вполне разумно, следует понимать, что в действительности она от времени не зависит. Надежность программного обеспечения является функцией числа ошибок, их серьезности и их расположения, а также того, как система используется».
Рассмотрим описание одной из самых известных ДЭМП модели Нельсона, который приводиттакое определение надежности ПО: «Надежность программы это вероятность безотказного выполнения n -прогонов программы». В основу построения модели Нельсона положены следующие допущения:
· машинная программа П может быть определена как описание некоторой вычисляемой функции F на множестве Е всех значений наборов входных данных, таких, что каждый элемент Еj множества Е представляет собой набор значений данных, необходимых для выполнения прогона программы, j = 1(1) N max, где N max – мощность множества Е;
· выполнение программы П приводит к получению для каждого Е j определенное значение функции F (Еj);
· множество Е определяет все возможные вычисления в программе П, т.е. каждому набору входных данных Еj соответствует некоторый прогон П и каждому прогону П соответствует некоторый набор входных данных Еj;
· наличие дефектов в программе соответствует тому, что на самом деле ей отвечает функция F *, отличная от заданной функции F;
· для некоторого набора в программе Еj отклонение выхода F *(Еj), полученного в результате выполнения программы от желаемого результата F (Еj), находится в пределах нормы Δ j
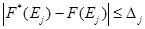; (6.12)
для всех остальных Ej, образующих подмножество Ее множества Е, выполнение программы П не обеспечивает приемлемого результата, т.е.
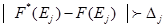(6.13)
при этом работа программы прекращается преждевременно или зацикливается.
Вероятность того, что произвольный прогон программы П будет правильным, т.е. выполняется условие (6.12), равна
,
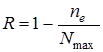где ne - общее число входных данных, соответствующих подмножеству Ее.
Для практической оценки величины показателя надежности программы предлагается следующая процедура.
Производится n прогонов программы, причем выбор входных данных должен соответствовать некоторым известным вероятностям реализации входных наборов - p j. Часть прогонов будет верной, а другая часть закончится отказами ПО. При этом процесс испытаний не должен прекращаться, а ошибки исправляться до завершения всех n прогонов. Тогда оценка показателя вероятности безотказной работы программы рассчитывается по формуле
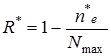, (6.14)
где ne * - количество ошибочных прогонов в серии из n испытаний,
R *- оценка вероятности безотказной работы ПО.
