Как следует из рисунка 5.1, на третьем этапе эксплуатационного цикла наблюдается прогрессирующий рост интенсивности отказов. Это объясняется проявлением износовых и других, носящих неизбежный характер, процессов, имеющих накопительный характер. В большинстве случаев проявления этих процессов в виде отказов хорошо подчиняются нормальному распределению, согласно которому плотность распределения отказов описывается уравнением:
 , (5.9)
, (5.9)
где f (T)- плотность распределения отказов за общее время эксплуатации Т;
s2 - дисперсия (стандартное отклонение) распределения;
s - среднеквадратическое отклонение;
М - математическое ожидание случайной величины (срок службы устройства).
При известной функции нормального распределения плотности отказов функция отказов имеет вид:
 . (5.10)
. (5.10)
Как следует из уравнений (5.9), (5.10), при этом виде распределения параметры надежности определяются уже двумя константами, а именно s и М. Это создает определенные неудобства при расчетах. На рисунке 5.4 представлены кривые, характеризующие параметры надежности при этом виде распределения.

Рисунок 5.4 – Кривые изменения функции отказов (а), плотности распределения (б) и интенсивности отказов (в) при нормальном законе распределения
При n отказов за время Т дисперсия определяется таким образом:
 . (5.11)
. (5.11)
Из теории вероятности известно, что кривые нормального распределения, имеющие различную пологость, должны иметь и различное среднеквадратическое отклонение. Например, если s 1 > s 2, кривая 1 будет иметь более пологий вид, чем кривая 2 (рисунок 5.5).
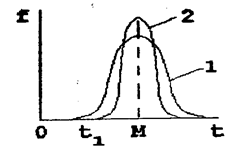
Рисунок 5.5 – Виды кривых распределения при s1 > s2
Следует помнить, что кривая f (T), как правило, отлична от нуля при начальном значении времени Т >>0, т.е. первоначально в системе возникают отказы, например, подчиняющиеся экспоненциальному распределению, а с момента времени t1 (рисунки 5.4, 5.5) появляются отказы, подчиняющиеся нормальному распределению.






