Расчет надежности систем на этапе эксплуатации

В период эксплуатации наиболее важными вопросами являются планирование и расчет периодов профилактик, а также планирование и расчет числа запасных элементов и блоков системы.

Планирование и расчет периодов профилактик

Профилактическое обслуживание – система предупредительных мер, направленных на снижение вероятности возникновения отказов (технические параметры, регулировки, замена комплектующих элементов, восстановление защитных покрытий и токопроводимых контактов и др.).

Профилактика преследует две цели:

– предупредить возникновение отказов;

– обнаружить такие отказы элементов изделия, которые не могли быть обнаружены средствами контроля в процессе эксплуатации и остались скрытыми, необнаруженными.

Профилактическое обслуживание может быть организовано по принципу обслуживания регламентного, календарного, а также комбинированного использования регламентного и календарного обслуживания.

Регламентное обслуживание – обслуживание, которое проводится по достижении параметрами изделия некоторых регламентированных показателей. Этот вид обслуживания применяется тогда, когда известна связь работоспособности и показателей некоторых технических параметров (силы тока, напряжения, сопротивления, яркости и т.д.).

Если же главный параметр, определяющий работоспособность изделий, – время, в течение которого изделие эксплуатируется или хранится, то профилактическое обслуживание назначается в строго определенные календарные сроки вне зависимости от состояния изделия. Такое обслуживание называется календарным.

В инженерной практике обычно связь работоспособности с показателями технических параметров, так же как и с временем использования, известна с некоторым приближением. Поэтому большее распространение получил комбинированный метод профилактического обслуживания.

В процессе эксплуатации параметры изделия контролируются, и по достижении ими критических значений производится профилактика. Профилактика производится и тогда, когда время, измеряемое от последней профилактики, достигает значения времени, календарно запланированного. Естественно, что время календарного обслуживания в этом случае может быть увеличено, поскольку существует некоторая вероятность предупреждения отказа.

Выбор контролируемых параметров и контролируемых элементов должен осуществляться по оптимальным маршрутам, т.е. в определенной последовательности с учетом информативности, которую дает каждая из проверок. Как правило, такие задачи решаются методами технической диагностики.

Календарное обслуживание осуществляется на основе изучения закономерностей отказов. Обычно, как уже показывалось ранее, интенсивность отказов изменяется с течением времени, что можно представить в виде графика (рис. 2.51).

На участке 0 – t ₁ преобладают отказы периода приработки и тренировки, на участке t ₁ – t ₂ – внезапные отказы (закон распределения времени до отказа – экспоненциальный), на участке от t ₂ и далее – отказы износового характера и старения (закон распределения времени до отказа – нормальный). Период времени 0 – t ₁ нельзя считать периодом нормальной эксплуатации, ему соответствует влияние скрытых дефектов производства. Профилактика, ориентированная на обеспечение надежности изделия с нормальными техническими характеристиками, начинается с момента времени t ₁.

Время профилактической проверки назначается исходя из следующих соображений. На участке t ₁ – t ₂, для которого l = const, время профилактики берется с учетом того, что вероятность появления отказа q не превышала допустимой вероятности q _доп (рис. 2.52).

Рис. 2.51. Изменение интенсивности Рис. 2.52. Выбор времени профилактики

отказов во времени

Известно, что для экспоненциального закона (подразд. 2.1.2, (2.16))

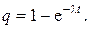
Отсюда

(2.134)

Пример 2.21. Определить время календарного обслуживания изделия, для которого l = 0,0001 1/ч, q _доп = 0,01,

ч.

На участке времени, превышающем t ₂, время профилактики определяется также исходя из того, что вероятность отказа не превышала допустимой вероятности.

На рис. 2.53 допустимая вероятность отказа q _доп представлена заштрихованной площадью, ограниченной f (x). Для определения времени календарного обслуживания изделия, ориентированного на замену деталей и блоков, выработавших ресурс, предварительно определяется среднее время работы до износового отказа Т и среднеквадратического отклонения . Тогда

(2.135)

где n – коэффициент при , соответствующий заданному значению q _доп (табл. 2.3).

Таблица 2.3

q _доп	0,01	0,02	0,04	0,05	0,06	0,08	0,10	0,12	0,16	0,20
n	2,526	2,323	2,053	1,960	1,880	1,750	1,643	1,554	1,404	1,282

Рис. 2.53. Допустимая вероятность отказа

Пример 2.22. Определить время замены блока изделия, если q _доп = = 0,01, Т = 120 ч, = 2 ч:

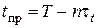= 120 – 2,526×2 = 115 ч.

Профилактическое обслуживание сложных системы начинается с планирования профилактических работ для простых устройств, входящих в нее. Сроки профилактики и ее содержание корректируются затем с учетом сложности систем.

Универсальных рекомендаций по оптимизации планирования профилактики не существует. В некоторых случаях целесообразно всю систему ставить на профилактику в одно и то же время и обеспечивать работу ее в полном составе в период между профилактическими обслуживаниями. В других случаях целесообразно ставить на профилактику отдельные элементы системы и обеспечивать ее непрерывную работу, хотя бы и не всегда в полном составе.

Характер изменения вероятности безотказного состояния P (t) под влиянием профилактического обслуживания в простейшем случае, когда возможно полное выявление отказных состояний, показан на рис. 2.54.

Рис. 2.54. Влияние профилактики на интенсивность отказов

Система начинает работу в момент времени 0 с вероятностью безотказного состояния, равной 1. С течением времени вероятность безотказного состояния снижается, и в момент времени t ₁ система будет поставлена на профилактику. К моменту окончания профилактики t ₂ вероятность безотказного состояния приближается к единице. Далее процесс повторяется.

Влияние профилактики на функциональную надежность изделия может быть определено следующей формулой:

(2.136)

где R (t) – вероятность выполнения изделием заданной функции на интервале t; K _ти(t) – коэффициент технического использования изделия с учетом проведения профилактики на интервале t; P (D t) – вероятность выполнения изделием заданной функции на интервале D t (использования изделий по назначению).

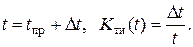(2.137)

P (D t) в первом приближении можно оценить по формуле

(2.138)

где l₀ – интенсивность отказов, обеспечиваемая данным объемом профилактики; D t – интервал использования изделия по назначению.

Планирование и расчет числа запасных изделий

Для обеспечения нормального функционирования изделий необходимо на весь период эксплуатации снабжать их запасным инструментом, принадлежностями, сменными комплектующими изделиями.

Запасом инструментов и принадлежностей (ЗИП) принято называть запас сменных изделий, материалов, инструментов и принадлежностей для обслуживания объектов.

Количество запасных частей зависит от интенсивности отказов от времени пополнения ЗИП (t _п), требуемой его достаточности (K _д), организации снабжения и степени восстановления.

Для пуассоновского потока отказов вероятность числа отказов n

(2.139)

Вероятность того, что число отказов за время t будет не больше m,

(2.140)

Вероятность того, что число отказов за время t будет больше m,

(2.141)

Если в ЗИП имеется два элемента, а вероятность того, что за время t_n произойдет больше двух отказов, равна 0,1, то это означает, что достаточность ЗИП равна 0,9 (K _д = 0,9), а недостаточность равна 0,1 (K _нд = 0,1). K _д ЗИП задается обычно равным 0,9 – 0,99.

Рассмотрим расчет числа запасных изделий для случая, когда отказавшие изделия не ремонтируются.

Организация ЗИП в данном случае реализуется по такой схеме. Неисправное комплектующее изделие заменяется исправным из ЗИП. Работоспособность его не восстанавливается. В ЗИП должно постоянно находиться такое число запасных частей, которое обеспечивает с заданной вероятностью достаточности (K _д) ЗИП потребность их для заданного интервала времени (t_n).

Исходными данными для расчета числа запасных частей являются:

· интенсивность отказов заменяемого изделия – l₀;

· число одинаковых заменяемых модулей или блоков в основном изделии – n;

· время пополнения ЗИП (время, до окончания которого не будет возможности пополнить ЗИП) – t_n;

· вероятность достаточности ЗИП – K _д.

Далее по формуле определяется K _д для различных значений числа запасных элементов в ЗИП, начиная с m = 0.

Как только коэффициент достаточности K _д превысит заданный, вычисления оканчиваются и последнее m берется в качестве рассчитанной цифры количества запасных частей (или блоков).

Пример 2.23. Определить число запасных типовых элементов замены (ТЭЗ), если известно, что l₀ = 5×10^–6 1/ч, K _д = 0,9...0,99, t_n = 5000 ч, число одинаковых ТЭЗ в аппаратуре равно 60 (n = 60).

Определим: 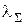= 5× 10^–6×60 = 3×10^–4, 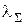t_n = 3×10^–4×5×10³ = 1,5.

Приводим вычисления:

при m = 0

;

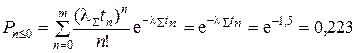при m = 1

;

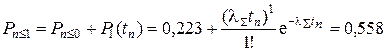при m = 2

;

при m = 3

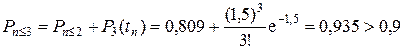
(для K _д = 0,9 достаточно иметь в ЗИП 3 ТЭЗ);

при m = 4

;

при m = 5

(для K _д = 0,99 достаточно иметь в ЗИП 5 ТЭЗ);

Рассмотрим расчет запасных изделий для восстанавливаемых элементов.

Схема использования ЗИП в этом случае показана на рис. 2.55.

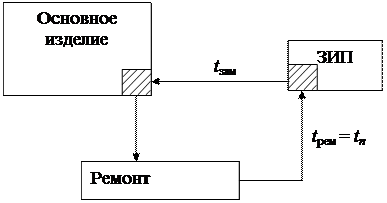
Рис. 2.55. Схема использования ремонтируемых ЗИП

Отказ элемента происходит с интенсивностью l₀. Отказавший элемент ремонтируется и поступает на пополнение в ЗИП. Среднее время ремонта в этом случае равно t_n, т.е. t_n существенно уменьшается. Методика расчета при этом та же, что и в предыдущем случае, только после окончания расчета количества запасных частей берется значение m + 1 (с учетом ремонтируемого ТЭЗ).

Пример 2.24. Решить предыдущий пример при условии, что ТЭЗ ремонтируется, время ремонта t _рем = 12 ч.

1/ч,

При m = 0

Поскольку вероятность того, что за время ремонта не произойдет отказа, больше достаточности K _д, то в ЗИП можно положить 0 + 1 = 1 ТЭЗ.

Выводы

Данная глава является, по существу, основной в учебном пособии. В ней авторы постарались рассмотреть максимальное количество проблем, связанных с расчетом надежности аппаратной части сложных технических систем. В то же время предлагаемые подходы к расчету надежности сильно адаптированы (упрощены), чтобы за сложностью решений не потерять основную нить методики.

Авторы обращали особое внимание на те факторы, с которыми на практике могут столкнуться специалисты при расчете надежности проектируемых или эксплуатируемых систем.

С точки зрения теории надежности системы делятся на восстанавливаемые и невосстанавливаемые. К невосстанавливаемым обычно относятся не сами системы, а их компоненты и, чаще всего, элементы, из которых состоят компоненты системы. Однако, если доступ к установленной системе затруднен, ее также можно рассматривать как невосстанавливаемую.

Характеристики надежности элементов иногда приходится определять статистически по результатам эксперимента, и тогда они представляются в таблично-графической форме. В этом случае на следующем этапе подбирается закон распределения, наилучшим образом описывающий полученные экспериментальные данные. Чаще всего, если экспериментальные данные тому резко не противоречат, выбирают экспоненциальный закон распределения как самый простой в использовании, хотя он и дает завышенную оценку надежности. Нормальный закон также достаточно часто используется в расчетах, при этом он дает заниженную оценку надежности. В данном учебном пособии в большинстве случаев в расчетах используется экспоненциальный закон распределения.

Если надежность, полученная по предварительным расчетам на этапе проектирования системы, оказывается ниже заданной, существует два пути повышения надежности: технологический, когда используют более надежные элементы (если такие существуют), и конструктивный – создание надежных систем из ненадежных элементов.

Конструктивный метод основан на резервировании в его разнообразных формах. Постоянно включенный резерв – это метод резервирования элементов системы. Резервирование замещением применяется для компонентов системы. Особое внимание в данном разделе уделено функциональному резервированию, как наиболее эффективному, так и наиболее сложному с точки зрения методики расчета.

Однако большинство систем относится к классу восстанавливаемых. Показатели надежности восстанавливаемых систем отличаются от показателей надежности невосстанавливаемых систем. Если для последних основной характеристикой является среднее время наработки на отказ, то для восстанавливаемых систем основная характеристика – коэффициент готовности, т.е. вероятность застать систему работоспособной в произвольный момент времени.

Для расчета коэффициента готовности выбран метод расчета по графу работоспособности как наиболее наглядный и потому лучше воспринимаемый, чем чисто математические методы. В основе графа работоспособности лежит марковская цепь, помеченная интенсивностями отказов и восстановлений отдельных блоков. Данный метод рассматривается для последовательного и параллельного соединения блоков. Многочисленные примеры позволят читателю в ряде случаев воспользоваться выведенными формулами.

С другой стороны, для сложных технических систем, состоящих из большого количества блоков, расчет по неусеченной марковской цепи становится на практике затруднительным из-за резко возрастающего со сложностью системы числа состояний. Для такой ситуации в пособии предлагается методика построения усеченной марковской сети, которая и демонстрируется при расчете надежности двух реальных технических систем.

Для повышения коэффициента готовности восстанавливаемой системы можно снизить интенсивность отказов, а можно повысить интенсивность восстановлений. Схемы встроенного контроля позволяют повысить интенсивность восстановления за счет сокращения времени обнаружения места неисправности системы. В данном учебном пособии рассмотрены различные варианты (схема встроенного контроля абсолютно надежна, схема встроенного контроля самопроверяемая, схема встроенного контроля несамопроверяемая).

На этапе проектирования редко можно получить точные надежностные характеристики отдельных блоков. Чаще характеристики задаются не детерминированно, т.е. интенсивность отказов и восстановлений задается в определенных пределах. Для этого случая рассмотрена модификация методики расчета коэффициента готовности на основе теории нечетких множеств, что позволяет выбрать вариант построения системы, оптимальный по соотношению «надежность-стоимость».

Основные проблемы этапа эксплуатации – это расчет периода профилактики и числа запасных блоков при возможности их ремонта и в отсутствии такой возможности. В данном учебном пособии эти вопросы рассмотрены скорее в обзорном порядке.

Вопросы и задания

1. Назовите показатели надежности невосстанавливаемых систем.

2. Для чего наряду с плотностью распределения отказов в теории надежности вводят интенсивность отказов?

3. Какие законы распределения случайных величин используются в теории надежности и почему?

4. Каковы недостатки и достоинства показательного распределения?

5. Если в технической документации указано, что для данного компонента системы среднее время наработки на отказ равно 100 000 ч, то чему равна интенсивность отказов этого элемента при показательном распределении?

6. Как при расчете надежности невосстанавливаемых систем учитываются режимы работы элементов?

7. Назовите существующие методы резервирования.

8. Какова методика расчета при постоянно включенном резерве?

9. Какие существуют виды резервирования замещением?

10. Сформулируйте критерий надежности систем с восстановлением.

11. Как определяются параметр потока отказов и параметр потока восстановлений?

12. Приведите пример графа работоспособности для простейшей системы из двух блоков, соединенных последовательно.

13. Является ли коэффициент готовности стационарным?

14. Приведите пример расчета стационарного коэффициента готовности для простейшей системы из двух блоков, соединенных параллельно.

15. Рассчитайте число состояний, входящих в марковскую цепь, если число блоков системы равно 10.

16. Как будет выглядеть усеченная марковская цепь из предыдущего вопроса, если в системе нет резервирования?

17. Каковы правила усечения марковской цепи, если в системе есть резервирование?

18. Как сказывается на коэффициенте готовности наличие в системе схем встроенного контроля?

19. Повышает или понижает надежность невосстанавливаемой системы схема встроенного контроля?

20. Чем можно воспользоваться при расчете надежности конструируемой системы, если надежностные характеристики отдельных блоков не могут быть точно определены?

21. Какие задачи решает теория надежности в период эксплуатации системы?

Список литературы

1. Белоусов В.В., Киселев В.В., Кулагина М.М. Надежность технических систем / Перм. гос. техн. ун-т. – Пермь, 1995. – 71 с.

2. Гуров С.В., Половко А.М. Основы теории надежности. – М.: BHV, 2008. – 704 с.

3. Шишмарев В.Ю. Надежность технических систем. – М.: Академия, 2010. – 304 с.

4. Белоусов В.В., Кон Е.Л., Кулагина М.М. Надежность средств и систем. Применение теории нечетких множеств и теории категорий для решения задач надежности, технической диагностики и телекоммуникации / Перм. гос. техн. ун-т. – Пермь, 2002. – 116 с.

5. Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. – М.: Горячая линия–Телеком, 2009. – 608 с.