Расчет надежности в условиях нечетко заданных исходных данных

Данный раздел посвящен проблеме расчета надежности сложных технических систем в процессе их проектирования при нечетко заданных исходных данных. Такая постановка задачи встречается в реальных усло­виях достаточно часто по двум причинам. Во-первых, надежностные ха­рактеристики отдельных блоков системы не всегда можно установить дос­таточно точно, в ряде случаев техническая документация дает разные зна­чения, а иногда они и вовсе не указаны, и проектировщику приходится ру­ководствоваться собственным опытом. Во-вторых, проектируемая система может работать в неблагоприятных условиях, и тогда реальные надежно­стные характеристики будут отличаться от тех, которые указаны в доку­ментации и справочной литературе.

Расчет надежности систем при нечетко заданных исходных данных практически не освещен в учебно-методической литературе, в отличие от стандартного расчета надежности системы при надежностных характери­стиках, заданных детерминированно. Учитывая изложенное, в данном раз­деле основной упор будет сделан не на методику расчета надежности, а на ее модификацию применительно к нечетко заданным исходным данным [4]. Для упрощения изложения в качестве примера проектируемой системы будет взят самый простой ее вариант, поскольку алгоритм расчета надеж­ности в условиях нечетко заданных исходных данных не зависит от слож­ности проектируемой системы.

Система может быть собрана из блоков различных типов. Надежно­стные характеристики блоков, составляющих систему, при этом рассмат­риваются как известные с определенной вероятностью. Достаточно хоро­шие возможности для этого предоставляет описание надежностных харак­теристик блока системы в форме нечеткого множества. Проектировщик (заказчик), задаваясь различными значениями, к примеру, среднего вре­мени наработки на отказ, формулирует степень своей уверенности в реали­зации каждого из них с помощью показателя, именуемого «степенью при­надлежности» и принимающего значения в диапазоне от 0 до 1 [1]. Чем хуже показатель с точки зрения надежности, тем выше степень уверенно­сти в его реализации.

Предполагается, что в проектируемой системе отсутствует аппарат­ная избыточность, т.е. встроенные технические средства повышения на­дежности, такие как резервирование или дублирование, а системы встро­енного функционального и тестового контроля обладают идеальными ха­рактеристиками: надежностью, полнотой контроля и глубиной локализа­ции. В этом случае надежностные показатели блоков и методика расчета системы зависят от того, является она восстанавливаемой или невосста­навливаемой.

Рассматриваемая в настоящем разделе задача проектирования фор­мулируется следующим образом: выбрать из нескольких заданных вариан­тов построения неизбыточной системы такой вариант, который минимизи­рует стоимость системы при надежности системы не хуже заданной.

Сформулируем алгоритм выбора (рис. 2.50).

Рис. 2.50. Алгоритм выбора оптимального варианта построения невосстанавливаемой системы в условиях нечеткого задания исходных данных

 

В соответствии с блоком 1 проектировщик определяет надежностные показатели блоков системы. В процессе определения показателей проекти­ровщик в соответствии с блоком 2 выясняет, будет ли интенсивности отка­зов задана детерминировано или нет? Если да, то выбор оптимального ва­рианта пойдет по левой ветви, если нет, то по правой. Последовательность шагов по левой и правой ветви в основном одинаковая. В блоках 3 (левая ветвь) и 6 (правая) выбираются возможные варианты построения системы. В блоках 4 (левая ветвь) и 7 (правая) рассчитываются надежностные пока­затели по каждому варианту построения системы. Далее при нечетко за­данных исходных данных в блоке 8 правой ветви по каждому варианту рассчитываются потери от неверного выбора исходных надежностных по­казателей. И, наконец, в блоках 5 (левая ветвь) и 9 (правая) выбирается оп­тимальный вариант построения системы. В предыдущем разделе в при­мерах 2.13 и 2.14 был рассмотрен расчет надежности систем, структура ко­торых уже была зафиксирована. Соответственно, в обоих случаях путь продвижения по алгоритму был: 1 – 2 – 4б.

Рассмотрим более сложные случаи реализации блоков данного алго­ритма для невосстанавливаемых и восстанавливаемых систем, когда есть несколько вариантов построения системы.

 

Выбор оптимального варианта для невосстанавливаемых систем

 

Для невосстанавливаемых систем основной характеристикой надеж­ности является среднее время наработки на отказ Т или интенсивность от­казов l, при этом обе характеристики связаны соотношением (2.16).

В качестве основной надежностной характеристики при формирова­нии исходного нечеткого множества выберем интенсивность отказов l, так как чем выше интенсивность отказов, тем выше уверенность в том, что ре­аль­ная интенсивность отказов не превысит заданную. Тогда нечеткое мно­же­ство интенсивности отказов для заданного блока будет выглядеть сле­дую­щим образом:

 

l = {(l₁ |b₁), (l₂ |b₂), …, (l _n |b _n)}, (2.127)

 

где l_{1, 2, …, n} – значение интенсивности отказов; b_{1,2, …, n} – вероятность того, что реальная интенсивность отказов не превысит заданную.

Пример 2.15. При определении интенсивности отказов для задан­ного блока проектировщик получил следующее множество:

 

l _i = {(1,35 × 10^–6|0,8), (2,80 × 10^–6|0,9), (4,60 × 10^–6|0,95)},

 

что означает: интенсивность отказа блока не превысит 1,35 × 10^–6 со степе­нью уверенности 0,8, не превысит 2,80 × 10^–6 со степенью уверенности 0,9 и не превысит 4,60 × 10^–6 со степенью уверенности 0,95.

Совокупность интенсивностей отказов для всех блоков образует мас­сив L.

В случае если проектировщику известна точная интенсивность отка­зов блока, нечеткое множество переходит в детерминированную характе­ристику блока системы и вместо правой ветви алгоритма проектировщик пойдет по левой.

Первый блок алгоритма – определение интенсивности отказов бло­ков системы – был проанализирован выше. Рассмотрим левую ветвь алго­ритма – выбор составляющих блоков системы по известным надежност­ным характеристикам возможных вариантов блоков, заданных детермини­ровано.

При построении системы имеется возможность выбора между одно­типными блоками с различными надежностными характеристиками и раз­личной стоимостью. Сначала рассмотрим пример выбора структуры сис­темы с детерминированно заданными характеристиками.

Пример 2.16. Пусть в вычислительной системе используется цен­тральный процессор и блок ОЗУ (см. рис. 2.25). Выбирать можно между двумя типами процессора, причем интенсивность отказов первого типа процессора 152 × 10^–6, стоимость его 60 у.е., а интенсивность отказов вто­рого типа процессора 250 × 10^–6, стоимость 40 у.е. Для ОЗУ также имеется выбор из двух типов, интенсивность отказов первого типа ОЗУ 64 × 10^–6, стоимость его 10 у.е., а интенсивность отказов второго типа процессора 80 × 10^–6, стоимость 8 у.е. Выбрать наименьший по стоимости вариант по­строения системы с интенсивностью отказов не выше 300 × 10^–6.

На первом этапе проводится полный перебор вариантов построения системы. Возможно 4 варианта построения системы:

1) процессор – тип 1; ОЗУ – тип 1;

2) процессор – тип 1; ОЗУ – тип 2;

3) процессор – тип 2; ОЗУ – тип 1;

4) процессор – тип 2; ОЗУ – тип 2.

Просчитаем интенсивность отказов по каждому из четырех вариан­тов в соответствии с методикой, приведенной в подразд. 2.1.5 (формула (2.26)):

1)l₁ = 1 × 152 × 10^–6 + 1 × 64 × 10^–6 = 216 × 10^–6,

2) l₂ = 1 × 152 × 10^–6 + 1 × 80 × 10^–6 = 232 × 10^–6,

3) l₃ = 1 × 250 × 10^–6 + 1 × 64 × 10^–6 = 314 × 10^–6,

4) l₄ = 1 × 250 × 10^–6 + 1 × 80 × 10^–6 = 330 × 10^–6.

 

Запишем интенсивности отказов и стоимости всех четырех вариан­тов:

 

1)l₁ = 216 × 10^–6, С = 70 у.е.;

2) l₂ = 232 × 10^–6, С = 68 у.е.;

3) l₃ = 314 × 10^–6, С = 50 у.е;

4) l₄ = 330 × 10^–6, С = 48 у.е.

 

По надежности нас устраивают первый и второй варианты, по стои­мости предпочтительным является второй вариант, как более дешевый.

Рассмотрим правую часть алгоритма, показанного рис. 2.50: расчет надежности системы по надежностным характеристикам составляющих ее блоков, заданных в форме нечеткого множества.

Пример 2.17. Рассмотрим систему из примера 2.16. Пусть интенсив­ность отказов двух вариантов центрального процессора и ОЗУ задана в форме нечеткого множества:

 

l_п1 = (140 × 10^–6|0,8; 152 × 10^–6|0,85; 160 × 10^–6|0,9),

l_п2 = (240 × 10^–6|0,7; 250 × 10^–6|0,85; 270 × 10^–6|0,9),

l_ОЗУ1 = (60 × 10^–6|0,8; 64 × 10^–6|0,9; 70 × 10^–6|0,95),

l_ОЗУ2 = (75 × 10^–6|0,85; 80 × 10^–6|0,9; 90 × 10^–6|0,95),

 

где l_п1, l_п2, l_ОЗУ1 и l_ОЗУ2 образуют в совокупности массив L.

Массив L формируем следующим образом. Выписываем все значе­ния вероятности задания исходных данных, входящие в данный массив. Одинаковые значения объединяем, оставшиеся выстраиваем по возраста­нию. Получим пять значений:

 

1) b₁ = 0,7; 2) b₂ = 0,8; 3) b₃ = 0,85; 4) b₄ = 0,9; 5) b₅ = 0,95.

 

Произведем разложение массива L на четкие подмножества b-уровня, руководствуясь следующим правилом:

 

(2.128)

 

где b – фиксированное значение вероятности из набора значений мас­сива L. При этом для каждого значения b рассматриваются все возможные варианты построения системы.

Для каждого из пяти вариантов построения системы значения интен­сивности отказов берутся по вышеуказанному алгоритму. Рассмотрим подробнее построение четких подмножеств для значения b = 0,7. Для пер­вого варианта (процессор типа 1, ОЗУ типа 1) в качестве интенсивности отказов процессора берется значение l_п1 = 140×10^–6, имеющее b = 0,8, по­скольку это ближайшая большая вероятность в ряду значений интенсивно­сти отказов для процессора типа 1. Для ОЗУ типа 1 берется l_ОЗУ1 = 60×10^–6, по той же самой причине и т.д.

В соответствии с этим алгоритмом четких множеств для b = 0,95 по­строить не удается, поскольку не для все типов процессора и ОЗУ есть на­дежностные характеристики с вероятностью, большей или равной 0,95.

Таким образом, четкие множества строятся для четырех значений вероятности:

 

1) b₁ = 0,7; 2) b₂ = 0,8; 3) b₃ = 0,85; 4) b₄ = 0,9.

 

В результате разбиений массива L получаем:

 

1) b₁ = 0,7: l_п1 = 140 × 10^–6; l_ОЗУ1 = 60 × 10^–6;

2) l_п1 = 140 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

3) l_п2 = 240 × 10^–6; l_ОЗУ1 = 60 × 10^–6;

4) l_п2 = 240 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

5) b₂ = 0,8: l_п1 = 140 × 10^–6; l_ОЗУ1 = 60 × 10^–6;

6) l_п1 = 140 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

7) l_п2 = 250 × 10^–6; l_ОЗУ1 = 60 × 10^–6;

8) l_п2 = 250 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

9) b₃ = 0,85: l_п1 = 152 × 10^–6; l_ОЗУ1 = 64 × 10^–6;

10) l_п1 = 152 × 10^–6; l_ОЗУ2 = 80 × 10^–6;

11) l_п2 = 250 × 10^–6; l_ОЗУ1 = 64 × 10^–6;

12) l_п2 = 250 × 10^–6; l_ОЗУ2 = 80 × 10^–6;

13) b₄ = 0,9: l_п1 = 160 × 10^–6; l_ОЗУ1 = 64 × 10^–6.

14) l_п1 = 160 × 10^–6; l_ОЗУ2 = 80 × 10^–6;

15) l_п2 = 270 × 10^–6; l_ОЗУ1 = 64 × 10^–6;

16) l_п2 = 270 × 10^–6; l_ОЗУ2 = 80 × 10^–6.

 

Далее проводим расчет надежности системы по каждому из полу­ченных шестнадцати вариантов исходных данных. Расчет надежности ве­дем в соответствии с методикой, изложенной в подразд. 2.1.5 (формула (2.26)).

Для шестнадцати вариантов проводим расчет надежности системы. Дополним полученные данные значениями стоимости С для каждого вари­анта:

 

1) b = 0,7; l = 200 × 10^–6; С = 70 у.е.;

2) b = 0,7; l = 215 × 10^–6; С = 68 у.е.;

3) b = 0,7; l = 300 × 10^–6; С = 50 у.е.;

4) b = 0,7; l = 315 × 10^–6; С = 48 у.е.;

5) b = 0,8; l = 200 × 10^–6; С = 70 у.е.;

6) b = 0,8; l = 215 × 10^–6; С = 68 у.е.;

7) b = 0,8; l = 310 × 10^–6; С = 50 у.е.;

8) b = 0,8; l = 325 × 10^–6; С = 48 у.е.;

9) b = 0,85; l = 216 × 10^–6; С = 70 у.е.;

10) b = 0,85; l = 232 × 10^–6; С = 68 у.е.;

11) b = 0,85; l = 314 × 10^–6; С = 50 у.е.;

12) b = 0,85; l = 330 × 10^–6; С = 48 у.е.;

13) b = 0,9; l = 224 × 10^–6; С = 70 у.е.;

14) b = 0,9; l = 240 × 10^–6; С = 68 у.е.;

15) b = 0,9; l = 334 × 10^–6; С = 50 у.е.;

16) b = 0,9; l = 350 × 10^–6; С = 48 у.е.

 

Из полученных результатов видно, что четвертые варианты построе­ния системы не обеспечивают заданную надежность ни при одном значе­нии b. Следовательно, их можно исключить из рассмотрения для умень­шения размерности задачи (это строки 4, 8, 12 и 16). Поэтому в дальней­шем мы будем работать с минимизированной таблицей, состоящей из сле­дующих двенадцати вариантов:

 

1) b = 0,7; l = 200 × 10^–6; С = 70 у.е.;

2) b = 0,7; l = 215 × 10^–6; С = 68 у.е.;

3) b = 0,7; l = 300 × 10^–6; С = 50 у.е.;

4) b = 0,8; l = 200 × 10^–6; С = 70 у.е.;

5) b = 0,8; l = 215 × 10^–6; С = 68 у.е.;

6) b = 0,8; l = 310 × 10^–6; С = 50 у.е.;

7) b = 0,85; l = 216 × 10^–6; С = 70 у.е.;

8) b = 0,85; l = 232 × 10^–6; С = 68 у.е.;

9) b = 0,85; l = 314 × 10^–6; С = 50 у.е.;

10) b = 0,9; l = 224 × 10^–6; С = 70 у.е.;

11) b = 0,9; l = 240 × 10^–6; С = 68 у.е.;

12) b = 0,9; l = 334 × 10^–6; С = 50 у.е.

 

Определив интенсивность отказов всех вариантов построения сис­темы, их стоимость и вероятность осуществления каждого варианта, можно провести оптимизацию выбора варианта построения системы. Оп­тимизацию будем проводить в два этапа. На первом этапе воспользуемся методом наименьших потерь [2].

Введем в рассмотрение эталонное решение Э, которое характеризу­ется минимальным значением интенсивности отказов l_Э и минимальным значением стоимости системы С_Э (при этом минимальное значение интен­сивности отказов l_Э должно быть меньше заданного техническими усло­виями для проектируемой системы).

Для данных из нашего примера эталонное решение будет характеризо­ваться следующими значениями: l_Э = 200×10^–6; С_Э = 50 у.е., где в качестве значения для интенсивности отказов и стоимости взяты мини­мальные значения из вышеприведенных.

Первое соотношение 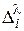будет характеризовать проигрыш в интен­сив­ности отказов данного варианта R_i по отношению к эталонному:

 

. (2.129)

 

Второе соотношение будет характеризовать проигрыш в стоимо­сти данного варианта R_i по отношению к эталонному:

 

. (2.130)

 

Проигрыш решения R_i по сравнению с эталонным (D _i) оценивается:

 

или

. (2.131)

 

Очевидно, что все значения потерь будут отрицательными, так как эталонный вариант является наилучшим из всех возможных. Поскольку нас интересует не знак, а абсолютная величина потерь, знак «минус» в дальнейших расчетах будет отброшен и все значения потерь будут рас­сматриваться по абсолютной величине.

Рассчитаем проигрыш по сравнению с эталонным вариантом для всех решений. Для первых двух вариантов расчет D _i покажем подробно, а для остальных просто запишем результаты:

 

1) b = 0,7; l = 200 × 10^–6; С = 70 у.е.; , ;

D _i = |(1 – 1,0) + (1 – 1,47)| = 0,47;

2) b = 0,7; l = 215×10^–6; С = 68 у.е.; ,

; D_i =| (1 – 1,075) + (1 – 1,417)| = 0,49;

3) b = 0,7; l = 300 × 10^–6; С = 50 у.е.; D _i = 0,54;

4) b = 0,8; l = 200 × 10^–6; С = 70 у.е.; D _i = 0,47;

5) b = 0,8; l = 215 × 10^–6; С = 68 у.е.; D _i = 0,54;

6) b = 0,8; l = 310 × 10^–6; С = 50 у.е.; D _i = 0,61;

7) b = 0,85; l = 216 × 10^–6; С = 70 у.е.; D _i = 0,57;

8) b = 0,85; l = 232 × 10^–6; С = 68 у.е.; D _i = 0,565;

9) b = 0,85; l = 314 × 10^–6; С = 50 у.е.; D _i = 0,73;

10) b = 0,9; l = 228 × 10^–6; С = 70 у.е.; D _i = 0,62;

11) b = 0,9; l = 240 × 10^–6; С = 68 у.е.; D _i = 0,61;

12) b = 0,9; l = 334 × 10^–6; С = 50 у.е.; D _i = 0,78.

Рассчитав потери на первом этапе для каждого варианта построения системы, определяем затем потери по сравнению с эталонным вариантом для каждого значения вероятности.

Из полученного списка вариантов видно, что для первых вариантов построения системы (процессор типа 1 и ОЗУ типа 1) потери для всех че­тырех вероятностей будут иметь следующие значения:

 

b = 0,7; D _i = 0,47;

b = 0,8; D _i = 0,47;

b = 0,85; D _i = 0,57;

b = 0,9; D _i = 0,62.

 

На втором этапе рассчитывается усредненное значение потерь для каждого варианта по следующей формуле:

 

, (2.132)

 

где n – количество значений вероятности, на которые был разбит исходный массив L. В качестве оптимального принимается вариант с минимальным значением потерь:

 

(2.133)

 

Просчитаем значения усредненной вероятности по формуле (2.132) для трех вариантов построения системы и значений вероятности, приве­денных в примере 2.17.

Для варианта 1

D = 0,7 × 0,47 + 0,8 × 0,47 + 0,85 × 0,57 + 0,9 × 0,62 = 1,7475.

Для варианта 2

D = 0,7 × 0,49 + 0,8 × 0,49 + 0,85 × 0,565 + 0,9 × 0,61 = 1,764.

Для варианта 3

D = 0,7 × 0,54 + 0,8 × 0,61 + 0,85 × 0,73 + 0,9 × 0,78 = 2,189.

В результате данного расчета в качестве оптимального следует при­нять первый вариант построения системы – процессор типа 1 и ОЗУ типа 1, имеющий минимальные потери по сравнению с эталонным вариантом.

В данном разделе был рассмотрен алгоритм выбора невосстанав­ли­ваемой системы, оптимальной по стоимости при надежности не хуже за­данной, в условиях нечетко заданных исходных данных. Как было пока­зано, задание исходных данных в виде нечеткого множества позволяет бо­лее точно отразить реальность. Расчеты по предложенному алгоритму (см. рис. 2.50) показывают, что оптимальный вариант, выбранный по идеализи­рованным (детерминированно заданным) исходным данным, может отли­чаться от оптимального варианта, выбранного по более реальным данным, представленным в виде нечеткого множества.

 

Выбор оптимального варианта для восстанавливаемых систем

 

Как было указано выше (подразд. 1.1.5), характеристики восстанав­ливае­мых систем отличаются от характеристик невосстанавливаемых сис­тем. Для установившегося режима работы восстанавливаемой системы (а именно этот режим рассматривается в настоящем пособии, см. подразд. 2.3.1.) имеют место пары: интенсивность отказов l/среднее время между отка­зами Т _о и интенсивность потока восстановлений m/среднее время вос­ста­новления Т _в.

При формировании исходного нечеткого множества будем зада­ваться интенсивностью отказов l_о и средним временем восстановления Т _в (величина, обратно пропорциональная интенсивности восстановлений l_в), так как чем выше значение интенсивности отказов и среднего времени восстановления, тем выше уверенность в том, что реальные поток отказов и среднее время восстановления не превысят заданные.

Пример 2.18. При определении потока отказов и среднего времени восстановления для заданного блока проектировщик получил следующее множество:

l_{о i} = {(1,35 × 10^–6|0,8), (2,80 × 10^–6|0,9), (4,60 × 10^–6|0,95)},

Т _{в i} = {(2,4|0,7), (2,8|0,8), (3,5|0,9)},

что означает: интенсивность отказа блока не превысит 1,35×10^–6 со степе­нью уверенности 0,8, не превысит 2,80 ×10^–6 со степенью уверенности 0,9 и не превысит 4,60 ×10^–6 со степенью уверенности 0,95. Аналогично читается и время восстановления.

Совокупность потоков отказов и времени восстановления для всех блоков образует массив L.

В случае если проектировщику известны точные данные об интен­сивности потока отказов и времени восстановления блока, нечеткое мно­жество переходит в детерминированную характеристику блока системы.

Таким образом, в зависимости от того, являются ли исходные дан­ные для расчета вероятностными или детерминированными, будут приме­няться разные способы расчета. Алгоритм же выбора оптимального вари­анта в целом изменяться не будет.

Первый блок алгоритма – определение интенсивности отказов бло­ков системы – был проанализирован выше. Рассмотрим левую ветвь алго­ритма – выбор составляющих блоков системы по известным надежност­ным характеристикам возможных вариантов сочетания блоков, заданных детерминированно.

При построении системы имеется возможность выбора между одно­типными блоками с различными надежностными характеристиками и раз­личной стоимостью. Перебор всех возможных вариантов построения сис­темы и составляет суть блока 3.

Пример 2.19. Пусть в вычислительной системе используется цен­тральный процессор и блок ОЗУ. Выбирать можно между двумя типами процессора, причем поток отказов первого типа процессора 152×10^–6, стоимость его 60 у.е., а поток отказов второго типа процессора 250×10^–6, стоимость 40 у.е. Время восстановления для обоих типов процессора оди­наково и равно 1 ч. Для ОЗУ также имеется выбор из двух типов, причем поток отказов первого типа ОЗУ 64×10^–6, стоимость его 10 у.е., а поток отказов второго типа процессора 80×10^–6, стоимость 8 у.е. Время восста­новления для обоих типов ОЗУ также одинаково и равно 0,5 ч.

Ставится следующая оптимизационная задача: выбрать наименьший по стоимости вариант построения системы с коэффициентом готовности не ниже 0,97.

На первом этапе проводится полный перебор вариантов построения системы. Возможны 4 варианта построения системы (блок 3):

1) процессор – тип 1; ОЗУ – тип 1;

2) процессор – тип 1; ОЗУ – тип 2;

3) процессор – тип 2; ОЗУ – тип 1;

4) процессор – тип 2; ОЗУ – тип 2.

Исследование надежности восстанавливаемых объектов (блок 4) про­водится по методике, описанной в подразд. 2.3.2.

Для приведенных исходных данных просчитаем коэффициент готов­ности в соответствии с системой (2.108) по каждому из четырех вариантов:

1) K _г = 0,98;

2) K _г = 0,975;

3) K _г = 0,95;

4) K _г = 0,945.

Далее среди вариантов, устраивающих нас с точки зрения надежно­сти, выбираем вариант, наименьший по стоимости (блок 5). Запишем ко­эффициенты готовности и стоимости двух устраивающих по надежности вариантов:

1) K _г = 0,98, С = 70 у.е.;

2) K _г = 0,975, С = 68 у.е.

С точки зрения стоимости предпочтительным является второй вари­ант, как более дешевый.

Рассмотрим правую часть алгоритма – расчет надежности системы по надежностным характеристикам составляющих ее блоков, заданных в форме нечеткого множества. Сначала вернемся к блоку 1 алгоритма рас­чета – определению вероятностных характеристик блоков системы.

Пример 2.20. Рассмотрим систему из примера 2.19. Пусть поток от­казов и среднее время восстановления двух вариантов центрального про­цессора и ОЗУ заданы в форме нечетких множеств:

l_п1 = (140 × 10^–6|0,8; 152 × 10^–6|0,85; 160 × 10^–6|0,9),

Т _{в п1} = (1,5|0,7; 2,0|0,8; 2,5|0,9),

l_п2 = (240 × 10^–6|0,7; 250 × 10^–6|0,85; 270 × 10^–6|0,9),

Т _{в п2} = (1,5|0,7; 2,0|0,8; 2,5|0,9),

l_ОЗУ1 = (60 × 10^–6|0,8; 64 × 10^–6|0,9; 70 × 10^–6|0,95),

Т _{в ОЗУ1} = (0,5|0,7; 1,0|0,8; 2,0|0,9),

l_ОЗУ2 = (75 × 10^–6|0,85; 80 × 10^–6|0,9; 90 × 10^–6|0,95),

Т _{в ОЗУ2} = (0,5|0,7; 1,0|0,8; 2,0|0,9),

где l_п1 , Т _{в п1}, l_п2 , Т _{в п2} , l_ОЗУ1, Т _{в ОЗУ1}, l_ОЗУ2 и Т _{в ОЗУ2} образуют в совокупности массив L. Массив L формируем следующим образом. Выписываем все значения вероятности, входящие в данный массив, одинаковые значения объединяем, оставшиеся выстраиваем по возрастанию. Получаем пять зна­чений:

 

1) b₁ = 0,7; 2) b₂ = 0,8; 3) b₃ = 0,85; 4) b₄ = 0,9; 5) b₅ = 0,95.

 

Произведем разложение массива L на четкие подмножества b-уровня (блок 6), руководствуясь вышеописанным правилом (2.128):

При этом для каждого значения b рассматриваются все возможные варианты построения системы.

Для каждого значения вероятности по каждому варианту построения системы значения потока отказов и времени восстановления берутся по вышеуказанному алгоритму. Рассмотрим подробнее построение четких подмножеств для значения b = 0,7. Для первого варианта (процессор типа 1, ОЗУ типа 1) в качестве потока отказов процессора берется значение l_п1 = 140 × 10^–6, имеющее b = 0,8, поскольку это ближайшая большая веро­ятность в ряду значений потока отказов для процессора типа 1. Для ОЗУ типа 1 берется l_ОЗУ1 = 60 × 10^–6, по той же самой причине. Среднее время восстановления для процессора берется равным 1,5, для ОЗУ – 0,5; оба эти значения имеют b = 0,7.

В соответствии с этим алгоритмом разбиения четких множеств для b = 0,95 построить не удается, поскольку не для всех типов процессора имеются надежностные характеристики с вероятностью, большей или рав­ной 0,95.

Таким образом, четкие множества строятся для четырех значений вероятности:

1) b₁ = 0,7; 2) b₂ = 0,8; 3) b₃ = 0,85; 4) b₄ = 0,9.

В результате разбиений массива L получаем:

1) b₁ = 0,7: l_п1 = 140 × 10^–6; l_ОЗУ1 = 60 × 10^–6;

Т _{в п1} = 1,5; Т _{в ОЗУ1} = 0,5;

2) l_п1 = 140 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

Т _{в п1} = 1,5; Т _{в ОЗУ2} = 0,5;

3) l_п2 = 240 × 0^–6; l_ОЗУ1 = 60 × 10^–6;

Т _{в п2} = 1,5; Т _{в ОЗУ1} = 0,5;

4) l_п2 = 240 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

Т _{в п2} = 1,5; Т _{в ОЗУ2} = 0,5;

5) b₂ = 0,8: l_п1 = 140 × 10^–6; l_ОЗУ1 = 60 × 10^–6;

Т _{в п1} = 2,0; Т _{в ОЗУ1} = 1,0;

6) l_п1 = 140 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

Т _{в п1} = 2,0; Т _{в ОЗУ2} = 1,0;

7) l_п2 = 250 × 10^–6; l_ОЗУ1 = 60 × 10^–6;

Т _{в п2} = 2,0; Т _{в ОЗУ1} = 1,0;

8) l_п2 = 250 × 10^–6; l_ОЗУ2 = 75 × 10^–6;

Т _{в п2} = 2,0; Т _{в ОЗУ2} = 1,0;

9) b₃ = 0,85: l_п1 = 152 10^–6; l_ОЗУ1 = 64 × 10^–6;

Т _{в п1} = 2,5; Т _{в ОЗУ1} = 1,5;

10) l_п1 = 152 × 10^–6; l_ОЗУ2 = 80 × 10^–6;

Т _{в п1} = 2,5; Т _{в ОЗУ2} = 1,5;

11) l_п2 = 250 × 10^–6; l_ОЗУ1 = 64 × 10^–6;

Т _{В П2} = 2,5; Т _{В ОЗУ1} = 1,5;

12) l_п2 = 250 × 10^–6; l_ОЗУ2 = 80 × 10^–6;

Т _{в п2} = 2,5; Т _{в ОЗУ2} = 1,5;

13) b₄ = 0,9: l_п1 = 160 × 10^–6; l_ОЗУ1 = 64 × 10^–6;

Т _{в п1} = 2,5; Т _{в ОЗУ1} = 1,5;

14) l_п1 = 160 × 10^–6; l_ОЗУ2 = 80 × 10^–6;

Т _{в п1} = 2,5; Т _{в ОЗУ2} = 1,5;

15) l_п2 = 270 × 10^–6; l_ОЗУ1 = 64 × 10^–6;

Т _{в п2} = 2,5; Т _{в ОЗУ1} = 1,5;

16) l_п2 = 270 × 10^–6; l_ОЗУ2 = 80 × 10^–6;

Т _{в п2} = 2,5; Т _{в ОЗУ2} = 1,5.

Далее проводим расчет надежности системы по каждому из полу­ченных шестнадцати вариантов исходных данных (блок 7). Расчет надеж­ности ведется в соответствии с методикой расчета надежности восстанав­ливаемых систем, изложенной при рассмотрении детерминированного за­дания исходных данных в примере 2.19.

Для шестнадцати представленных вариантов проводим расчет коэф­фициента готовности системы. Дополним полученные данные значениями стоимости для каждого варианта:

1) b = 0,7; K _г = 0,99; С = 70 у.е.,

2) b = 0,7; K _г = 0,98; С = 68 у.е.,

3) b = 0,7; K _г = 0,96; С = 50 у.е.,

4) b = 0,7; K _г = 0,95; С = 48 у.е.,

5) b = 0,8; K _г = 0,99; С = 70 у.е.,

6) b = 0,8; K _г = 0,98; С = 68 у.е.,

7) b = 0,8; K _г = 0,96; С = 50 у.е.,

8) b = 0,8; K _г = 0,95; С = 48 у.е.,

9) b = 0,85; K _г = 0,98; С = 70 у.е.,

10) b = 0,85; K _г = 0,97; С = 68 у.е.,

11) b = 0,85; K _г = 0,95; С = 50 у.е.,

12) b = 0,85; K _г = 0,94; С = 48 у.е.,

13) b = 0,9; K _г = 0,97; С = 70 у.е.,

14) b = 0,9; K _г = 0,96; С = 68 у.е.,

15) b = 0,9; K _г = 0,90; С = 50 у.е.,

16) b = 0,9; K _г = 0,88; С = 48 у.е.

С целью уменьшения размерности задачи проведем минимизацию этих данных: вычеркнем варианты построения системы, для которых при всех вероятностях исходных данных коэффициент готовности получается меньше заданного. В данном случае это варианты 3 и 4. В результате оста­ется восемь вариантов:

1) b = 0,7; K _г = 0,99; С = 70 у.е.,

2) b = 0,7; K _г = 0,98; С = 68 у.е.,

3) b = 0,8; K _г = 0,99; С = 70 у.е.,

4) b = 0,8; K _г = 0,98; С = 68 у.е.,

5) b = 0,85; K _г = 0,98; С = 70 у.е.,

6) b = 0,85; K _г = 0,97; С = 68 у.е.,

7) b = 0,9; K _г = 0,97; С = 70 у.е.,

8) b = 0,9; K _г = 0,96; С = 68 у.е.

Строка номер восемь остается в системе, поскольку она соответст­вует второму варианту построения системы, который для других значений b дает коэффициент готовности не хуже 0,97.

Определив интенсивность отказов данного варианта построения сис­темы, его стоимость и вероятность осуществления такого варианта, можно провести оптимизацию выбора варианта построения системы. Оптимиза­цию будем проводить в два этапа. На первом этапе (блок 8) снова восполь­зуемся методом наименьших потерь [2].

Как и выше, введем в рассмотрение эталонное решение Э, которое характеризуется максимальным значением коэффициента готовности K _{г э} и минимальным значением стоимости системы С_э.

Для вариантов нашего примера эталонное решение будет характеризо­ваться следующими значениями: K _э = 0,99; С_э= 48 у.е.

Первая характеристика будет характеризовать проигрыш по коэф­фициенту готовности данного варианта R_i по отношению к эталон­ному (2.86), вторая характеристика 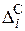будет характеризовать проигрыш по стоимости данного варианта R_i по отношению к эталонному (2.130).

Проигрыш решения R_i по сравнению с эталонным – D _i – оценивается опять же по соотношению (2.131):

 

 

Рассчитаем проигрыш по сравнению с эталонным вариантом для всех решений. Для первых двух вариантов расчет D _i покажем подробно, а для остальных просто запишем результаты:

1) b = 0,7; K _г = 0,99; С = 70 у.е.,

; ,

D _i = |(1 – 1,0) + (1 – 1,47)| = 0,47;

2) b = 0,7; K _г = 0,98; С = 68 у.е.,

; ,

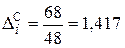D _i =|(1 – 0,99) + (1 – 1,417)| = 0,407;

3) b = 0,8; K _г = 0,99; С = 70 у.е.; D _i = 0,47;

4) b = 0,8; K _г = 0,99; С = 68 у.е.; D _i = 0,54;

5) b = 0,85; K _г = 0,99; С = 70 у.е.; D _i = 0,57;

6) b = 0,85; K _г = 0,99; С = 68 у.е.; D _i = 0,565;

7) b = 0,9; K _г = 0,99; С = 70 у.е.; D _i = 0,62;

8) b = 0,9; K _г = 0,99; С = 68 у.е.; D _i = 0,61.

Рассчитав потери на первом этапе для каждого варианта построения системы, можно определить потери по сравнению с эталонным вариантом для каждого значения вероятности.

Из сравнения полученных восьми вариантов видно, что в первом вари­анте построения системы (процессор типа 1 и ОЗУ типа 1) потери для всех четырех вероятностей будут иметь следующие значения:

b = 0,7; D _i = 0,47;

b = 0,8; D _i = 0,47;

b = 0,85; D _i = 0,57;

b= 0,9; D _i = 0,62.

На втором этапе (блок 9) рассчитывается усредненное значение по­терь для каждого варианта по формуле (2.132).

В качестве оптимального принимается вариант с минимальным по абсолютной величине значением потерь (2.133):

 

Просчитаем значения усредненной вероятности для вариантов по­строения системы и значений вероятности.

Для варианта 1

D = 0,7 × (0,47) + 0,8 × (0,47) + 0,8 × (0,57) + 0,9 × (0,62) = 1,7475.

Для варианта 2

D = 0,7 × (0,407) + 0,8 × (0,54) + 0,85 × (0,565) + 0,9 × (0,61) = 1,763.

В результате данного расчета в качестве оптимального следует при­нять первый вариант построения системы – процессор типа 1 и ОЗУ типа 1, поскольку усредненные потери для варианта 1 оказываются меньше ус­редненных потерь для варианта 2.

Таким образом, из приведенного анализа и сравнения примеров видно, что детерминированный подход к решению сформулированной выше задачи и подход к расчету на основе представления данных в виде нечеткого множества дают разные результаты.

Проанализировав методику расчета надежности для простейших не­восстанавливаемых и восстанавливаемых систем, можно сделать следую­щие выводы.

Традиционное детерминированное задание исходных данных явля­ется идеализированным и не позволяет учесть при проектировании сис­темы специфику возможного изменения надежностных характеристик от­дельных блоков. Задание исходных данных в форме нечеткого множества представляется более приближенным к реальным условиям расчета надеж­ности и выбору оптимального по критерию надежность/стоимость вари­анта проектируемой системы.

Методика расчета надежности для систем с различной надежностной конфигурацией при точном (детерминированном) задании исходных дан­ных принципиально не изменяется при переходе к заданию исходных дан­ных в форме нечеткого множества. Нами показано, что существенные из­менения претерпевают блоки общего алгоритма выбора оптимального ва­рианта построения системы, связанные с определением надежностных ха­рактеристик модулей в составе системы, при задании их исходных данных в форме нечеткого множества. В частности, изменяется исходный этап оп­ределения надежностных характеристик отдельных блоков (блок 1, см. рис. 2.46), когда приходится выбирать, какие конкретно характеристики являются наиболее подходящими для представления в форме нечеткого множества, как это показано при рассмотрении соответствующих блоков общего алгоритма для невосстанавливаемых и восстанавливаемых систем (соответственно примеры 2.16 и 2.17 и примеры 2.19 и 2.20).