Сущность приближенного метода расчета надежности мостиковых схем методом исключения элементов заключается в том, что в структурной схеме выбираются один или несколько элементов и затем производится расчет показателей надежности для двух крайних случаев:
1) предполагается, что выбранные элементы абсолютно надежны (вероятность безотказной работы элементов равна единице);
2) предполагается, что выбранные элементы абсолютно ненадежны (вероятность безотказной работы элементов равна нулю);
В первом случае две точки системы, к которым подключается элемент, соединяются постоянной связью, во втором – между этими точками отсутствует какая-либо связь. Для двух полученных структур определяются вероятности безотказной работы, соответственно равные 
и 
.
Затем определяется средневзвешенное значение вероятностей безотказной работы исключаемых элементов
(5.42)
где p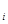 
– вероятность безотказной работы I-го исключаемого элемента; n – число исключаемых элементов
Окончательно вероятность безотказной работы системы определяется по формуле
(5.43)
Очевидно, если р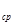 
=1 (абсолютно надежные исключаемые элементы), то 
. Если 
=0 (абсолютно ненадежные элементы), то 
.
Особенности метода исключения элементов:
• с увеличением числа исключаемых элементов точность расчетов понижается;
• с увеличением числа элементов в системе при фиксированном числе исключаемых элементов точность расчетов повышается;
• в качестве исключаемых элементов целесообразно выбирать элементы, имеющие высокую надежность.
Пример 5.7.
Определить приближенно вероятность безотказной работы системы представленной на рис 5.18, двумя методами: преобразованием треугольника в звезду и исключением элементов.
Вероятности безотказной работы всех элементов одинаковы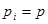 
=0,9.
рис.5.18.
