Пояснения к работе. Стандартная методика обработки результатов многократных измерений достаточно трудоемка, при этом далеко не всегда можно выполнить серию измерений

Стандартная методика обработки результатов многократных измерений достаточно трудоемка, при этом далеко не всегда можно выполнить серию измерений, объем которой достаточен для выявления закона распределения случайной составляющей погрешности. Кроме того, если неисключенный остаток систематической погрешности сравнительно велик, то выполнение большой серии измерений для максимального снижения случайной составляющей погрешности теряет смысл.

Упрощенная процедура обработки результатов многократных прямых измерений применяется при числе измерений n < 30. При использовании этой методики за результат измерения как обычно принимается среднее арифметическое результатов исправленного ряда измерений, которое вычисляют по формуле:

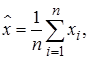(4.1)

где x_i – i -й исправленный результат измерения;

– среднее арифметическое исправленного ряда измерений;

n – число результатов измерений.

Для расчета среднего квадратического отклонения результата измерения используется формула:

(4.2)

Среднее квадратическое отклонение является основной характеристикой размера случайных погрешностей результата измерений.

Для нахождения границ доверительного интервала случайной погрешности измерений в конкретном случае рекомендуется проанализировать априорную информацию об объекте измерений и условиях проведения измерений. Если явных причин, способных привести к отклонению распределения результатов измерений от нормального закона не выявлено, то доверительные границы находят с помощью квантилей распределения Стьюдента по формулам:

(4.3)

(4.4)

где х _н и х _в – соответственно координаты нижней и верхней границ доверительного интервала;

t – квантиль распределения Стьюдента. Значения квантиля в зависимости от числа измерений n и доверительной вероятности Р _д приведены [1].

Если на результат измерений оказывает влияние только случайная составляющая погрешности, то этот результат представляют в виде: ; х _н; х _в; Р _д.

Часто имеет место ситуация, когда на результат измерений оказывают влияние две составляющие: погрешность средства измерений и случайная составляющая погрешности, зависящая от внешних факторов. Погрешность средства измерений определяется по его классу точности, а случайная оценивается с помощью приведенной выше методики. В этом случае при определении результирующей погрешности измерений возникает задача суммирования погрешностей. В теории измерений показывается, что в случае независимых составляющих погрешности справедливо следующее соотношение:

(4.5)

где ∆_Σ – результирующая погрешность, Δ₁ и Δ₂ – составляющие погрешности, причем, если модуль одной из составляющих превышает модуль другой составляющей более чем в 8 раз, то влиянием меньшей составляющей на результирующую погрешность можно пренебречь.

Если доверительная вероятность для погрешности средства измерений не указана, то при расчетах ее можно принимать равной 95 %. Результат измерений представляют в виде: ; Р _д. При этом числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и значение погрешности ∆_Σ.

По мере увеличения числа измерений вклад случайной составляющей погрешности в окончательный результат уменьшается и наступает момент, когда случайной составляющей можно пренебречь. В этом случае дальнейшее увеличение количества измерений бессмысленно. При планировании эксперимента необходимо заранее определить необходимое количество измерений, обеспечивающее требуемую точность. В противном случае трудоемкость измерений может оказаться неоправданно высокой.